Dreiseitige Pyramide Volumen Rechner

Mit unserem Rechner für das Volumen dreiseitiger Pyramiden kannst du das Volumen jeder Pyramide mit dreieckiger Grundfläche bestimmen, unabhängig davon, ob du die Größe der Grundfläche kennst oder nicht. Wenn du das Volumen einer rechtwinkligen Dreieckspyramide oder eines regelmäßigen Tetraeders bestimmen möchtest, bist du hier genau richtig.
Du möchtest lernen, wie du das Volumen einer dreiseitigen Pyramide schriftlich bestimmen kannst? Lies weiter, um sowohl die Formel als auch Beispiele, wie du sie anwenden kannst, zu erfahren.

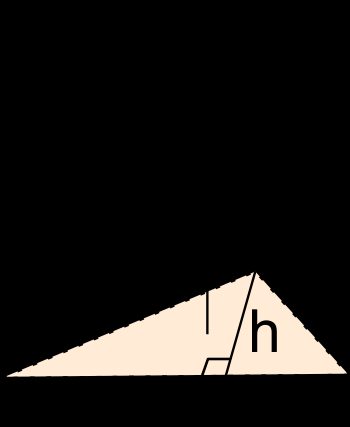
Eine Dreieckspyramide ist ein fester Gegenstand, der durch die Verbindung einer dreieckigen Basis mit einem Punkt S (Spitze) entsteht. Dadurch entstehen vier Flächen, von denen jede ein Dreieck bildet. Wenn du die Pyramide drehst, kann jede Seite die Basis der Pyramide sein. Die Gerade, die senkrecht zur Basis steht und durch den Scheitelpunkt verläuft, wird als Höhe der Pyramide bezeichnet.

Hier ist das dunkelblaue Dreieck die Basis der Pyramide und die gestrichelte schwarze Gerade ist die Höhe:

Um den Rechner für das Volumen dreiseitiger Pyramiden zu verwenden, befolge diese Schritte:

1. Kennst du die Fläche der Pyramidenbasis?

• Wenn ja, gib sie in den Rechner ein.
• Wenn nicht, überprüfe, welche Daten du über die Grundfläche kennst: wähle die entsprechende Option in unserem Rechner aus und gib deine Daten ein. Die Grundfläche wird dann für dich berechnet.

2. Gib die Höhe der Pyramide ein.

3. Der Rechner zeigt dir dann sofort das Volumen der Pyramide an :)

Die Volumenformel für eine dreiseitige Pyramide lautet:

V = A ∙ H / 3,

wobei:

• V — das Volumen einer dreieckigen Pyramide ist,
• A — die Fläche der Pyramidenbasis ist, und
• H — die Höhe von der Basis bis zur Spitze ist.

In Worten ausgedrückt: das Volumen einer dreieckigen Pyramide ist ein Drittel des Produkts aus der Grundfläche mal der Höhe der Pyramide.

Um das Volumen einer Dreieckspyramide mit einer Höhe von 10 cm und einer rechtwinkligen Grundfläche mit den Seitenlängen 3 cm, 4 cm und 5 cm zu bestimmen:

1. Bestimme den Flächeninhalt der Grundfläche: In unserem Fall ist das 3 ∙ 4 / 2 = 6.
2. Ermittle die Höhe der Pyramide: In unserem Fall beträgt sie 10.
3. Wende die Formel für das Volumen einer dreiseitigen Pyramide an: 6 ∙ 10 / 3 = 20.
4. Das Volumen der Pyramide beträgt 20 cm³.

Der schwierigste Schritt ist in der Regel die Berechnung der Grundfläche — um mehr darüber zu erfahren, kannst du unseren allgemeinen Dreiecksflächenrechner oder einen der Rechner für die einzelnen Dreieckstypen benutzen:

• Gleichseitiges Dreieck Rechner,
• Gleichschenkliges Dreieck Rechner oder
• Fläche eines rechtwinkligen Dreiecks Rechner.

Wenn du wissen möchtest, wie du das Volumen einer Dreieckspyramide (regelmäßiges Tetraeder) oder einer rechtwinkligen Dreieckspyramide bestimmen kannst, dann schau dir die beiden nächsten Abschnitte an, in denen wir die entsprechenden Formeln zeigen.

Eine dreiseitige Pyramide mit gleichseitigen Dreiecken als Seitenflächen wird regelmäßiges Tetraeder genannt.

Das Volumen eines Tetraeders mit der Seitenlänge a kann wie folgt berechnet werden:

V = a³ ∙ √2 / 12,

was ungefähr V = a³ ∙ 0,12 entspricht.

Das Volumen eines Tetraeders mit einer Seitenlänge von 6 cm ist zum Beispiel:

V = 6³ ∙ √2 / 12 = 18 √2,

was gerundet 6³ ∙ 0,12= 25,92 ist.

Eine Pyramide ist senkrecht, wenn ihr Scheitelpunkt direkt über dem Schwerpunkt der Basis liegt, andernfalls ist sie schräg. Wenn die Basis außerdem ein gleichseitiges Dreieck ist, gelten die folgenden Formeln für die Berechnung des Volumens:

• Wenn die Grundfläche die Seitenlänge a hat und die Höhe der Pyramide H ist, dann:

  V = a² ∙ H ∙ √3 / 12.

• Wenn die Basis die Seitenlänge a hat und die Kanten zwischen Basis und Spitze die Länge b haben, können wir mithilfe des Satzes des Pythagoras die Höhe der Pyramide und dann das Volumen ermitteln:

  V = √(b² - a²/3) ∙ a² ∙ √3 / 12.

Bestimme die Seitenlänge eines Tetraeders aus seinem Volumen:

1. Multipliziere das Volumen mit 12.
2. Dividiere das Ergebnis durch √2 ≈ 1,41
3. Ziehe die Kubikwurzel.
4. Das war's! Du hast die Seitenlänge deines Tetraeders gefunden.

Die Antwort lautet 1,6654 ∙ ∛Volumen. Wir erhalten dieses Ergebnis, indem wir die Formeln zusammenführen: Höhe = √(2/3) ∙ Seitenlänge und Volumen = a³ ∙ √2 / 12, was zu der Formel Höhe = √(∛576 / 3) ∙ ∛Volumen führt. Näherungsweise erhalten wir, wie behauptet, Höhe ≈ 1,6654 ∙ ∛Volumen.