Zuletzt aktualisiert: 27. Jul 2024

Flächeninhalt rechtwinkliges Dreieck Rechner

Q: Wie groß ist der Flächeninhalt eines rechtwinkligen Dreiecks mit einer Hypotenuse von 5 cm und einem Winkel von 45°?

Der Flächeninhalt beträgt 6,25 . Wir erhalten diese Antwort, indem wir die Formel Flächeninhalt = c² ∙ sin(α) ∙ cos(α) / 2 mit c = 5 und α = 45° anwenden. Der mathematische Lehrsatz, mit dem diese Formel hergeleitet wird, heißt Sinusgesetz .

Q: Wie nennt man die Seiten eines rechtwinkligen Dreiecks?

Die beiden Seiten, die senkrecht zueinander stehen, werden Schenkel genannt. Die Seite gegenüber dem rechten Winkel (also die längste Seite) ist die Hypotenuse .

Erstellt von Hanna Pamuła, Doktorand*in

Überprüft von Bogna Szyk

Übersetzt von Luise Schwenke

Luise Schwenke

Luise works as a German translator and Calculatorian at Omni. She holds a degree in Food Engineering from the University of Sciences - Neubrandenburg, Germany, and specialized her career in biotechnology. She worked in human genetic diagnostics, developing and producing pharmaceutical products for clinical phase 2 and 3 studies. She is always hungry for new fields to learn about that allow her to combine her creative and analytical thinking. Currently, she is getting her hands on coding, focusing on data science and big data. Luise spent an academic year in Brazil and loves traveling the world to experience and learn from different cultures. See full profile

Check our editorial policy

und Julia Kopczyńska, promovierend

Julia Kopczyńska

PhD candidate, Polish Academy of Sciences

LinkedInResearch Gate

A microbiologist with a low-key addiction to coffee. Since her Bachelor’s, she has focused on the gut microbiome and its role in human health. Now she hopes to find the golden bacteria to improve gut health in her Ph.D. project. She enjoys scientific writing and digging really deep into a topic. She has been living in 5 different countries and loves to travel to new places. In her free time, she likes to be active by playing volleyball, biking, and going for long walks. See full profile

Check our editorial policy

Neu

Inhalt

Formeln für den Flächeninhalt eines rechtwinkligen Dreiecks Flächeninhalt eines gleichschenkligen rechtwinkligen Dreiecks Wie man den Flächeninhalt eines rechtwinkligen Dreiecks mit unseren Rechner ermittelt FAQs

Wenn du dich fragst, wie man den Flächeninhalt eines rechtwinkligen Dreiecks ermittelt, bist du hier genau richtig – dieser Flächeninhalt-eines-rechtwinkligen-Dreiecks-Rechner ist dein Werkzeug.

Egal, ob du die Gleichung für die Schenkel des Dreiecks, den Schenkel und die Hypotenuse oder die Seite und den Winkel suchst, du wirst nicht enttäuscht sein – dieser Rechner hat sie alle eingebaut.

Scrolle nach unten, um mehr über die Formeln für den Flächeninhalt des rechtwinkligen Dreiecks zu erfahren, oder probiere unseren Rechner direkt aus!

Formeln für den Flächeninhalt eines rechtwinkligen Dreiecks

🙋 Wenn du gerade festgestellt hast, dass dein Dreieck kein rechtwinkliges Dreieck ist, schau dir diesen allgemeinen Fläche Dreieck Rechner an.

Die Grundgleichung ist eine umgeformte Version der Standardformel für die Höhe eines Dreiecks ( $a \cdot h / 2$ ). Da die Schenkel des rechtwinkligen Dreiecks rechtwinklig zueinander stehen, wird ein Schenkel als Basis genommen und der andere als Höhe des rechtwinkligen Dreiecks:

\text{Fläche}=\frac{a\cdot b}{2}

Manchmal ist es nicht ganz so offensichtlich – du hast andere Werte als die zwei Schenkel angegeben; was dann?

Wenn du einen Schenkel und die Hypotenuse kennst, kannst du den Satz des Pythagoras anwenden, um den fehlenden Schenkel zu finden:

\qquad a^2+b^2=c^2

Berechne dann die Quadratwurzel der umgeformten Gleichung:

Aus $a$ und $c$ ergibt sich: $b = \sqrt{c^2 - a^2}$ :

\qquad\text{Fläche}=a\cdot\frac{\sqrt{c^2-a^2}}{2}

Mit $b$ und $c$ berechnen wir, dass $a = \sqrt{c^2 - b^2}$ :

\qquad \text{Fläche} = b\cdot\frac{\sqrt{c^2-b^2}}{2}

Wenn du einen Winkel und die Hypotenuse kennst, kannst du das Sinusgesetz auf dieses Dreieck anwenden:

\qquad a=c\cdot\sin(\alpha)

Also:

\qquad \begin{split} b&=c\cdot\sin(\beta)\\&=c\cdot\sin(90\degree-\alpha)\\ &=c\cdot\cos(\alpha) \end{split}

Daher:

\qquad \text{Fläche}=c^2\cdot\sin(\alpha)\cdot\frac{\cos(\alpha)}{2}

Bestimme den Flächeninhalt bei bekanntem Winkel und einem Schenkel z. B. mit trigonometrischen Funktionen:

\qquad\frac{a}{b}=\tan(\alpha)

Und:

\qquad\frac{b}{a}=\tan(\beta)

Wir erhalten:

\qquad \begin{split} \text{Fläche}&=b\cdot\tan(\alpha)\cdot\frac{b}{2}\\ \\[1.5em] &=b^2\cdot\frac{\tan(\alpha)}{2} \end{split}

oder:

\qquad \begin{split} \text{Fläche}&=a\cdot a\cdot \frac{\tan(\beta)}{2}\\[1em] &=a^2\cdot\frac{\tan(\beta)}{2} \end{split}

🙋 Möchtest du mehr über rechtwinklige Dreiecke wissen? Dann besuche unseren Rechtwinkliges Dreieck Rechner!

Flächeninhalt eines gleichschenkligen rechtwinkligen Dreiecks

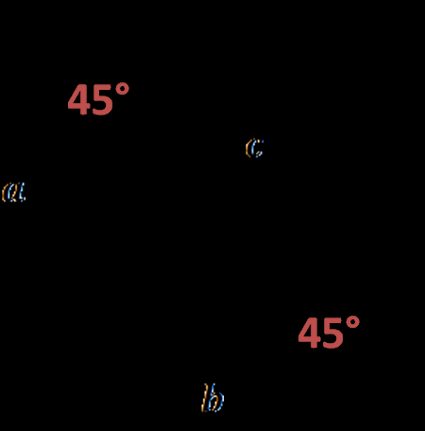
Ein gleichschenkliges rechtwinkliges Dreieck ist ein spezielles rechtwinkliges Dreieck, das manchmal auch als 45-45-90 Dreieck bezeichnet wird (es ist so speziell, dass wir extra ein Tool dafür entwickelt haben, den 45-45-90 Dreiecksrechner). In einem solchen Dreieck sind die Schenkel gleich lang (da die Hypotenuse immer die längste der rechtwinkligen Dreiecksseiten sein muss):

a=b

Ein Schenkel ist die Basis, der andere die Höhe – zwischen ihnen liegt ein rechter Winkel. Der Flächeninhalt eines gleichschenkligen, rechtwinkligen Dreiecks ist also:

\text{Fläche}=\frac{a^2}{2}

Wie man den Flächeninhalt eines rechtwinkligen Dreiecks mit unseren Rechner ermittelt

Lass uns die Berechnung Schritt für Schritt durchgehen:

Wähle eine Option aus, je nachdem, was du angegeben hast. Angenommen, wir kennen einen Schenkel und einen Winkel, dann ändern wir die Auswahl im Rechner auf Gegebener Winkel und eine Seite.
Gib die Werte ein. Wir wissen zum Beispiel, dass $\alpha = 40\degree$ und $b$ $17\ \text{cm}$ ist.
Sieh zu, wie unser Flächeninhalt-eines-rechtwinkligen-Dreiecks-Rechner alle Berechnungen für dich durchführt! Der Flächeninhalt des gewählten Dreiecks beträgt $121,\!25\ \text{cm}^2$ .

FAQs

Wie berechne ich den Flächeninhalt eines rechtwinkligen Dreiecks bei gegebenen Seiten?

Die Methode hängt davon ab, welche Seiten du gegeben hast:

Wenn du die beiden Schenkel kennst, dann benutze die Formel Fläche = a ∙ b / 2, wobei a und b die Schenkel sind.
Wenn du einen Schenkel a und die Hypotenuse c kennst, benutze die Formel: Flächeninhalt = a ∙ √(c² - a²) / 2.

Wie groß ist der Flächeninhalt eines rechtwinkligen Dreiecks mit einer Hypotenuse von 5 cm und einem Winkel von 45°?

Der Flächeninhalt beträgt 6,25. Wir erhalten diese Antwort, indem wir die Formel Flächeninhalt = c² ∙ sin(α) ∙ cos(α) / 2 mit c = 5 und α = 45° anwenden. Der mathematische Lehrsatz, mit dem diese Formel hergeleitet wird, heißt Sinusgesetz.

Woher weiß ich, ob ein Dreieck rechtwinklig ist?

Wenn du drei Seiten eines Dreiecks hast und wissen möchtest, ob dieses Dreieck rechtwinklig ist, überprüfe, ob der Satz des Pythagoras gilt: a² + b² = c², wobei c die längste Seite (Hypotenuse) ist und a und b die zwei anderen Seiten sind.

Wie nennt man die Seiten eines rechtwinkligen Dreiecks?

Die beiden Seiten, die senkrecht zueinander stehen, werden Schenkel genannt. Die Seite gegenüber dem rechten Winkel (also die längste Seite) ist die Hypotenuse.