Rechtwinkliges Dreieck Rechner

Unser Rechner für rechtwinklige Dreiecke hilft dir, die Längen der Seiten eines rechtwinkligen Dreiecks zu bestimmen. Dieser Dreiecksrechner zeigt dir auch, wie du den Flächeninhalt eines rechtwinkligen Dreiecks bestimmen kannst und gibt dir viele Informationen über die praktischen Anwendungen eines rechtwinkligen Dreiecks.

Als Erstes wollen wir dir erklären, was ein rechtwinkliges Dreieck überhaupt ist. Die Definition ist sehr einfach und mag für diejenigen, die sie bereits kennen, sogar offensichtlich erscheinen: Ein rechtwinkliges Dreieck ist ein Dreieck, bei dem genau ein Winkel 90° hat. Die anderen beiden Winkel sind eindeutig kleiner als der rechte Winkel, denn die Summe aller Winkel in einem Dreieck beträgt immer 180°.

Die Seiten eines rechtwinkligen Dreiecks haben spezielle Namen. Die Seite, die dem rechten Winkel gegenüberliegt, ist immer die längste im Dreieck und wir nennen sie „Hypotenuse“. Die anderen beiden Seiten werden Katheten genannt. Die Hypotenuse und die Katheten stehen in einer besonderen Beziehung zueinander – wir werden sie uns gleich genauer anschauen, wenn wir über den Satz des Pythagoras sprechen.

Wenn du nur die Hypotenuse eines rechtwinkligen Dreiecks berechnen willst, kannst du es mit diesem Rechner für rechtwinklige Dreiecke tun. Wir empfehlen dir aber auch ein Tool, welches wir speziell dafür bei Omni Calculators entwickelt haben: den Hypotenuse Rechner. Die Hypotenuse liegt dem rechten Winkel gegenüber und mithilfe des Satzes des Pythagoras kannst du ihre Länge finden. Für ein rechtwinkliges Dreieck mit den Katheten a und b und der Hypotenuse c besagt der Satz des Pythagoras, dass a² + b² = c².

Um c zu bestimmen, ziehst du die Quadratwurzel aus beiden Seiten und erhältst c = √(b²+a²)`. Wir können diese Erweiterung des Satzes des Pythagoras auch als eine „Hypotenusenformel“ betrachten. Der Satz des Pythagoras Rechner ist ebenfalls ein hervorragendes Hilfsmittel zur Berechnung der Hypotenuse.

Lösen wir nun ein praktisches Beispiel, wie man die Hypotenuse eines rechtwinkligen Dreiecks ohne Taschenrechner (oder Omni-Rechner) berechnen könnte:

1. Bestimme die Werte von a und b.
2. Nimm a und b zum Quadrat.
3. Addiere die beiden Werte: a² + b².
4. Ziehe die Quadratwurzel aus dem Ergebnis.
5. Die Quadratwurzel liefert einen positiven und einen negativen Wert. Da es sich um Längen handelt, ignoriere das negative Ergebnis.
6. Der sich ergebende Wert ist der Wert der Hypotenuse c.

Schauen wir uns nun an, wie das Verfahren mit einem der Rechner von Omni aussehen würde, zum Beispiel mit diesem Rechner für rechtwinklige Dreiecke:

1. Gib den Wert von a und b in den Taschenrechner ein.
2. Du erhältst sofort den Wert von c.
3. Zusätzlich erhältst du den Wert des Flächeninhalts eines solchen Dreiecks.

Wir haben bereits gesehen, dass die Berechnung des Flächeninhalts eines rechtwinkligen Dreiecks mit dem Rechner für rechtwinklige Dreiecke sehr einfach ist. Bei Omni Calculators haben wir auch einen Rechner, der speziell für diesen Zweck entwickelt wurde: den Rechner für die Fläche eines rechtwinkligen Dreiecks. Schauen wir uns nun etwas genauer an, wie man den Flächeninhalt von rechtwinkligen Dreiecken berechnet.

Die Methode zur Ermittlung des Flächeninhalts eines rechtwinkligen Dreiecks ist ganz einfach. Alles, was du brauchst, sind **die Länge der Basis und die Höhe
**. In einem rechtwinkligen Dreieck sind die Basis und die Höhe die beiden Seiten, die den rechten Winkel bilden. Da die Multiplikation dieser beiden Werte die Fläche des entsprechenden Rechtecks ergeben würde und das Dreieck die Hälfte davon ist, lautet die Formel:

Fläche = ½ ∙ Grundfläche ∙ Höhe.

Wenn du die Basis oder die Höhe nicht kennst, kannst du sie mit dem Satz des Pythagoras ermitteln. Probiere den Rechner für rechtwinklige Dreiecke aus, um deine Berechnungen zu überprüfen, oder wenn du mit größeren oder dezimalen Werten arbeiten musst.

Sehen wir uns nun andere Parameter eines rechtwinkligen Dreiecks an, die man mithilfe anderer Tools von Omni berechnen kann. Die Seiten eines Dreiecks haben eine bestimmte Steigung oder Neigung. Die Formel für die Steigung lautet

Steigung = (y₂ - y₁)/(x₂ - x₁).

Wenn also die Koordinaten (1,-6) und (4,8) sind, ist die Steigung der Strecke (8 + 6)/(4 - 1) = 14/3. Wenn du wissen willst, ob ein Dreieck rechtwinklig ist und nur seine Koordinaten kennst, nutze diese einfache Methode: Schau, ob das Produkt der Steigungen zweier (die Seiten des Dreiecks enthaltenden) Linien gleich -1 ist.

Mit der Winkelumrechnung kannst du ganz einfach Winkel von Bogenmaß in Grad und von Grad in Bogenmaß umrechnen:

• Wenn ein Winkel im Bogenmaß ist – multipliziere den Wert mit 180/π; und
• Wenn ein Winkel in Grad angegeben ist – multipliziere den Wert mit π/180.

Manchmal kannst du auf ein Problem stoßen, bei dem zwei oder sogar drei Seitenlängen fehlen. In solchen Fällen helfen dir der Rechner für rechtwinklige Dreiecke, der Rechner für die Hypotenuse und die Methode zur Bestimmung des Flächeninhalts eines rechtwinkligen Dreiecks nicht weiter. Du musst trigonometrische Funktionen verwenden, um diese fehlenden Werte zu finden.

Das rechtwinklige Dreieck ist nur eines der vielen besonderen Dreiecke, die es gibt. Diese Dreiecke haben ein oder mehrere besondere Merkmale, die sie einzigartig machen. Wie wir zum Beispiel gesehen haben, hat das rechtwinklige Dreieck einen rechten Winkel und damit eine Hypotenuse, was es zu einem einzigartigen Dreieck macht. Neben dem rechtwinkligen Dreieck gibt es noch andere besondere Dreiecke mit interessanten Eigenschaften.

Eines der bekanntesten speziellen Dreiecke ist das gleichseitige Dreieck, das drei gleich lange Seiten hat und dessen Winkel alle 60° haben. Das macht es viel einfacher, einen Rechner zur Lösung eines solchen Dreiecks zu entwickeln.

Ein weiteres spezielles Dreieck ist das gleichschenklige Dreieck, bei dem zwei Seiten gleich lang sind und damit auch zwei seiner Winkel gleich groß sind. Im Gegensatz zu gleichseitigen Dreiecken gibt es gleichschenklige Dreiecke in vielen verschiedenen Formen.

Es gibt noch viele andere besondere Dreiecke. Wir werden uns jetzt aber ein paar ganz besondere rechtwinklige Dreiecke ansehen, die nicht nur rechtwinklig sind, sondern auch andere einzigartige Eigenschaften haben, welche sie interessant machen.

Das sogenannte „45-45-90“-Dreieck ist ein ganz spezielles Dreieck der besonderen rechtwinkligen Dreiecke. Es ist ein rechtwinkliges Dreieck, das auch ein gleichschenkliges Dreieck ist. Seine beiden Katheten sind gleich lang und es hat außerdem die Eigenschaft, dass die nicht-rechten Winkel genau halb so groß sind wie der rechte Winkel (deshalb nennen wir diese Art Dreieck „45-45-90“-Dreieck).

So ein rechtwinkliges Dreieck entsteht durch das Teilen eines Quadrats entlang seiner Diagonale. Deshalb sind beide Katheten (Seiten des Quadrats) gleich lang. Wenn du mehr über dieses besondere rechtwinklige Dreieck wissen möchtest, empfehlen wir dir den 45-45-90 Dreiecksrechner, der speziell für diesen Zweck entwickelt wurde.

Ein weiteres faszinierendes Dreieck aus der Gruppe der besonderen rechtwinkligen Dreiecke ist das sogenannte „30-60-90“-Dreieck. Der Name kommt daher, dass es einen rechten Winkel (90°) hat, dann einen Winkel von 30° und einen weiteren von 60°. Diese Winkel sind aufgrund der Werte ihrer trigonometrischen Funktionen (Kosinus, Sinus, Tangens usw.) besonders. Welche Bedeutung das hat, kannst du in unserem 30-60-90 Dreiecksrechner nachlesen, aber für diejenigen, die zu faul sind, auf den Link zu klicken, fassen wir hier einige Informationen zusammen. Angenommen, die kürzere Seite hat die Länge a, dann ergibt sich ein Dreieck, bei dem:

1. die zweite Länge gleich a√3 ist;
2. die Hypotenusenlänge 2a beträgt;
3. der Flächeninhalt gleich (a²√3)/2 ist;
4. der Umfang a(3 + √3) beträgt.

Auf den ersten Blick mag es so aussehen, als hätten ein rechtwinkliges Dreieck und ein Parallelogramm nichts gemeinsam. Wie kann ein Dreiecksrechner dir helfen, ein Parallelogramm zu verstehen? In Wirklichkeit kann jedes Parallelogramm in 2 oder mehr rechtwinklige Dreiecke zerlegt werden. Nehmen wir das Rechteck als Beispiel, um es zu veranschaulichen.

Stell dir ein Rechteck vor, irgendein Rechteck. Zeichne nun eine gestrichelte Linie auf einer der Diagonalen dieses Rechtecks. Wenn wir das Rechteck durch die Diagonale trennen, erhalten wir zwei rechtwinklige Dreiecke. Wenn du dir die Dreiecke ansiehst, brauchst du den Rechner für rechtwinklige Dreiecke nicht zu benutzen, um zu sehen, dass beide gleich groß sind, d. h. ihre Flächeninhalte sind identisch. Das bedeutet, dass der Flächeninhalt des Rechtecks doppelt so groß ist wie die der Dreiecke.

Wenn wir über die Gleichungen nachdenken, ergibt dies Sinn, denn der Flächeninhalt eines Rechtecks mit den Seiten a und b ist genau Flächeninhalt = a ∙ b, während für das rechtwinklige Dreieck Flächeninhalt = Grundseite ∙ Höhe / 2 gilt, was in diesem Fall Flächeninhalt = a ∙ b /2 bedeuten würde. Das ist genau das, was wir bereits gesehen haben, als wir das Rechteck einfach an der Diagonale geschnitten haben.

Das war ein einfaches Beispiel eines Rechtecks, aber dasselbe gilt auch für die Fläche eines Quadrats. Bei anderen Parallelogrammen wird das Verfahren etwas komplizierter (es kann bis zu 4 rechtwinklige Dreiecke unterschiedlicher Größe beinhalten). Mit ein bisschen Geschick kannst du jedoch die gleiche Idee anwenden und den Flächeninhalt eines Parallelogramms mit rechtwinkligen Dreiecken berechnen. Du kannst natürlich auch noch effizienter sein und einfach unseren Rechner benutzen.

Geometrie und Polygone, insbesondere Dreiecke, sind nicht auseinander zu halten. Die Eigenschaften einiger Dreiecke, wie z. B. rechtwinkligen Dreiecke, sind meist interessant und schockierend, selbst für Nicht-Mathematiker. Wir werden uns jetzt eine interessante Art von Tupeln ansehen, welche sehr eng mit rechtwinkligen Dreiecken verbunden ist und welche die Mathematiker lieben – und du vielleicht bald auch.

Diese Zahlenmengen werden Pythagoreische Tripel genannt und sind Mengen von 3 ganzen Zahlen (nennen wir sie a, b und c), die den Satz des Pythagoras erfüllen: a² + b² = c². Das heißt, wir könnten ein rechtwinkliges Dreieck mit den Seitenlängen a, b und c bilden. Die Anzahl der Zahlen, die diese Beziehung erfüllen, ist begrenzt, aber Mathematiker haben Spaß daran, nach neuen Kombinationen zu suchen.

Abgesehen vom Kuriositätsfaktor dieser Beziehung hat sie einige interessante Eigenschaften, die in der Kryptografie genutzt werden. Angesichts der Anwendungen, die man für solche Zahlenmengen finden kann, haben Mathematiker sogar noch weiter geforscht und Mengen von 4, 5... und mehr Elementen definiert, die eine ähnliche Beziehung erfüllen: Die Summe der Quadrate aller Zahlen bis auf eine ist gleich dem Quadrat der übrig gebliebenen Zahl.

In engem Zusammenhang mit dem Pythagoreisches Tripel steht auch der berüchtigte Große Fermatscher Satz, in dem der fast schon legendäre kryptische Mathematiker Pierre Fermat feststellte, dass es keine Menge von drei ganzzahligen Zahlen geben kann, welche die folgende Beziehung erfüllen: aⁿ + bⁿ = cⁿ für n größer als 2. Diese Vermutung wurde mathematisch erst 1995 bewiesen, mehr als 300 Jahre nachdem sie formuliert wurde und gilt als eines der wichtigsten mathematischen Probleme des Jahrhunderts.

Wir haben schon viel über Dreiecke, insbesondere über rechtwinklige Dreiecke, und ihre Anwendungen in der Mathematik und Geometrie gesprochen. Worüber wir noch nicht gesprochen haben, ist der Nutzen von rechtwinkligen Dreiecken für die Berechnungen im echten Leben. Es mag den Anschein haben, dass die Anwendungen außerhalb der Geometrie begrenzt sind, aber sehen wir uns einmal die Schatten an.

Ja, Schatten. Die Schatten, die ein Objekt wirft, wenn es beleuchtet wird. Wenn du dir die Form ansiehst, die der Schatten, das Objekt und der Boden bilden, wirst du feststellen, dass es sich tatsächlich um ein rechtwinkliges Dreieck handelt! Zumindest in dem Fall, wenn das Objekt vollkommen senkrecht und der Boden waagerecht ist. Meistens ist das der Fall, oder zumindest nahe genug dran. Das bedeutet, dass wir den Rechner für rechtwinklige Dreiecke benutzen können, um verschiedene Informationen über Objekte unter der Sonne zu finden. Schauen wir mal, wie das geht.

Stell dir vor, du hast ein Gebäude, von dem wir die Höhe wissen wollen, aber du kannst sie nicht direkt messen, weil es zu hoch ist, um ein Maßband vom Dach fallen zu lassen. Was du tun kannst, ist die Länge des Schattens auf der Straße zu messen. Dann kannst du mit einem beliebigen Winkelmessgerät und einem Blatt Papier den Winkel zwischen dem Schatten und dem Boden ermitteln. Wenn du weißt, dass der Winkel zwischen dem Gebäude und dem Boden 90° beträgt, kannst du den Wert der Höhe des Gebäudes ermitteln.

Mit dieser Technik kannst du die Höhe vieler Objekte messen, solange du einen hellen Sonnentag oder eine andere Lichtquelle hast, die das Objekt beleuchten. Tatsächlich war dies früher eine sehr gängige Messtechnik. Die wohl interessanteste und verblüffendste Anwendung von rechtwinkligen Dreiecken ist die von Eratosthenes, der es schaffte, mithilfe von rechtwinkligen Dreiecken und Schatten den Radius der Erde zu messen – wir erklären jetzt, wie er das gemacht hat.

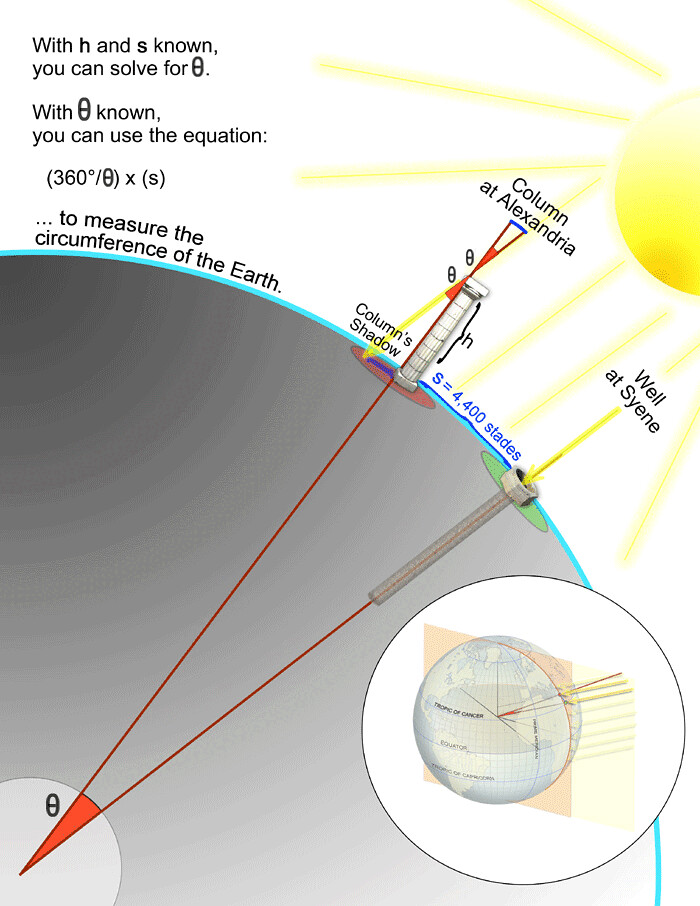
Eratosthenes bemerkte, dass es zur Sommersonnenwende einen Ort auf der Erde gab, an dem die Brunnen zur Mittagszeit keinen Schatten hatten, d.h. die Sonne schien direkt auf sie herab. Als er dies bemerkte, stellte er eine Säule mit bekannter Höhe in bekannter Entfernung von diesem Brunnen auf und maß die Größe des Schattens, den die Säule am Mittag des Sonnenwendtages erzeugte. Mithilfe von rechtwinkligen Dreiecken und Trigonometrie konnte er dann den Winkel (mit dem Erdmittelpunkt als Winkelscheitel) zwischen dem Brunnen und der Säule, sowie den Radius der Erde anhand der bekannten Entfernung zwischen diesen beiden Punkten bestimmen.

Das war eine erstaunliche Leistung, die du jetzt viel einfacher mit den Omni-Rechnern, die wir für dich entwickelt haben, erbringen kannst.