Quadratwurzel Rechner

Unser Quadratwurzel-Rechner schätzt die Quadratwurzel aus jeder positiven Zahl, die du möchtest. Gib einfach die gewünschte Zahl ein und lies die Ergebnisse ab. Alles wird schnell und automatisch berechnet! Mit diesem Tool kannst du auch das Quadrat der gewünschten Zahl schätzen (gib den Wert einfach in das zweite Feld ein) und damit perfekte Quadrate aus der Quadratwurzel-Formel finden.

Kämpfst du mit dem Addieren, Subtrahieren, Multiplizieren, Dividieren oder Vereinfachen von Quadratwurzeln? Damit ist jetzt Schluss! Im folgenden Text lernst du, wie du diese Operationen durchführen kannst.

Hast du dich jemals gefragt, woher das Quadratwurzel-Symbol √** stammt? Wir können dir versichern, dass seine Geschichte nicht so einfach ist, wie du anfangs vielleicht denkst. Der Ursprung des Wurzelsymbols geht bis in die Antike zurück, genauso wie der Ursprung des Prozents — lies weiter, um mehr zu erfahren!

Wenn du nach dem Graphen der Quadratwurzel oder den Eigenschaften der Quadratwurzelfunktion suchst, gehst du direkt zu dem entsprechenden Abschnitt (klicke einfach auf die Links oben!). Dort erklären wir dir, wie du die Ableitung einer Quadratwurzel berechnest; wir gehen auch darauf ein, wie du die Quadratwurzeln von Exponenten oder Brüchen berechnest. Wenn du hartnäckig genug bist, wirst du schließlich herausfinden, dass es tatsächlich möglich ist, die Quadratwurzel aus einer negativen Zahl zu ziehen. Dazu brauchen wir komplexe Zahlen, die in der Physik und Mathematik eine breite Anwendung finden.

Quadratwurzeln waren schon im Altertum bekannt. Die früheste Tontafel mit dem korrekten Wert von √2 = 1,41421 bis zu 5 Dezimalstellen stammt aus Babylonien (1800 v. Chr. - 1600 v. Chr.). Viele andere Dokumente zeigen, dass Quadratwurzeln auch von den alten Ägyptern, Indern, Griechen und Chinesen verwendet wurden. Der Ursprung des Wurzelsymbols √ ist jedoch noch weitgehend spekulativ.

• Viele Gelehrte glauben, dass Quadratwurzeln vom Buchstaben "r" abstammen — dem ersten Buchstaben des lateinischen Wortes radix, das Wurzel bedeutet.
• Eine andere Theorie besagt, dass das Symbol der Quadratwurzel vom arabischen Buchstaben ج stammt, der in seiner ursprünglichen Form ﺟ im Wort جذر — Wurzel — vorkommt (die arabische Sprache wird von rechts nach links geschrieben).

Bei der ersten Verwendung des Quadratwurzel-Symbols √ fehlte der horizontale "Balken" über den Zahlen innerhalb des Quadratwurzel- (oder Radikal-)Symbols √‾. Der "Balken" heißt auf Lateinisch vinculum und bedeutet Bindung. Obwohl das Radikalsymbol mit vinculum heute im alltäglichen Gebrauch ist, wird es oft weggelassen, z. B. in Online-Texten. Die Notation von Wurzeln höheren Grades wurde von Albert Girard eingeführt, der den Gradindex in die Öffnung des Radikalzeichens setzte, z. B. ³√ oder ⁴√.

Wir haben erklärt, wie das Wurzelsymbol √ entstanden ist, aber warum werden Wurzeln überhaupt so genannt? Die Wahl des Namens "Wurzel" wird deutlicher, wenn wir die Gleichung x = ⁿ√a als xⁿ = a umformulieren. Die Zahl x wird Wurzel oder Radikal genannt, weil sie die versteckte Basis von a ist. Das Wort Radikal bedeutet also nicht weitreichend oder extrem, sondern grundlegend, die Wurzel erreichend.

Was ist mit dem "quadratischen" Teil im Namen der "Quadratwurzeln"? Geometrisch gesehen ist die Quadratwurzel √x die Seitenlänge eines Quadrats mit dem Flächeninhalt x - daher der Name. Ebenso wird die dritte Wurzel ∛ oft "Kubikwurzel" genannt, weil ∛x die Kantenlänge eines Würfels mit dem Volumen x ist. So sind Quadratwurzeln in der ebenen Geometrie allgegenwärtig, während Kubikwurzeln in der dreidimensionalen Geometrie häufig vorkommen. Das Auftauchen von Wurzeln in einfachen geometrischen Problemen erklärt, warum Radikale schon vor mehreren tausend Jahren für die Menschheit von Interesse waren.

In der Mathematik sind die traditionellen Operationen mit Zahlen Addition, Subtraktion, Multiplikation und Division. Manchmal kommen jedoch noch weitere Operationen hinzu: Quadratwurzeln**, Potenzierung und Logarithmus. In diesem Artikel konzentrieren wir uns auf das Quadrieren von Quadratwurzeln.

Die Definition der Quadratwurzel einer gegebenen Zahl x ist jede Zahl y, deren Quadrat y² = y × y die ursprüngliche Zahl x ergibt. Beachte, dass auch y² = (-y) × (-y) gilt. Die Quadratwurzel-Formel lässt sich also wie folgt ausdrücken:

y = ±√x ⟺ y² = x

dabei ist ⟺ ein mathematisches Symbol, das wenn und nur wenn bedeutet. Jede positive reelle Zahl hat immer zwei verschiedene Quadratwurzeln — die erste ist positiv, die zweite negativ. Im Gegensatz dazu hat die 0 nur eine Wurzel - sich selbst. Denke daran, dass wir mit dem Symbol √x immer die nicht-negative Wurzel von x bezeichnen!

Es gibt noch eine andere gebräuchliche Art, Quadratwurzeln zu bezeichnen, die die Quadratwurzel in Form einer Bruchpotenz ausdrückt:

√x = x^1/2 = x^0,5

Der Grund für diese Schreibweise ist, dass:

(x^0.5)² = x^{0.5 × 2} = x

Vielleicht sind wir nicht sehr bescheiden, aber wir denken, dass die beste Antwort auf die Frage, wie man Wurzeln quadrieren kann, ganz einfach ist: Benutze den Quadratwurzel-Rechner! Du kannst ihn sowohl auf deinem Computer als auch auf deinem Smartphone benutzen, um schnell die Quadratwurzel berechnen zu können. Leider gibt es manchmal Situationen, in denen du dich nur auf dich selbst verlassen kannst. Was dann? Um dich darauf vorzubereiten, solltest du dir einige grundlegende perfekte Quadratwurzeln merken:

• Quadratwurzel aus 1: √1 = 1, denn 1 ∙ 1 = 1;

• Quadratwurzel aus 4: √4 = 2, denn 2 ∙ 2 = 4;

• Quadratwurzel aus 9: √9 = 3, da 3 ∙ 3 = 9;

• Quadratwurzel von 16: √16 = 4, da 4 ∙ 4 = 16;

• Quadratwurzel von 25: √25 = 5, da 5 ∙ 5 = 25;

• Quadratwurzel von 36: √36 = 6, da 6 ∙ 6 = 36;

• Quadratwurzel von 49: √49 = 7, da 7 ∙ 7 = 49;

• Quadratwurzel aus 64: √64 = 8, da 8 ∙ 8 = 64;

• Quadratwurzel aus 81: √81 = 9, da 9 ∙ 9 = 81;

• Quadratwurzel aus 100: √100 = 10, da 10 ∙ 10 = 100;

• Quadratwurzel von 121: √121 = 11, da 11 ∙ 11 = 121; und

• Quadratwurzel aus 144: √144 = 12, da 12 ∙ 12 = 144.

Die oben genannten Zahlen sind die einfachsten Quadratwurzeln, denn jedes Mal erhältst du eine ganze Zahl. Versuche, sie dir zu merken! Aber was kannst du tun, wenn es eine Zahl gibt, die nicht so eine schöne Quadratwurzel hat? Es gibt mehrere Lösungen. Erstens kannst du versuchen, das Ergebnis durch Testen vorherzusagen. Nehmen wir an, du möchtest die Quadratwurzel von 52 bestimmen:

1. Du weißt, dass √49 = 7 und √64 = 8 ist, also sollte √52 zwischen 7 und 8 liegen.

2. Die Zahl 52 liegt näher an der 49 (tatsächlich näher an der 7), also kannst du schätzen, dass √52 7,3 ist.

3. Dann quadrierst du 7,3 und erhältst 7,3² = 53,29 (wie die Quadratwurzel-Formel sagt), was größer ist als 52. Du musst es also mit einer kleineren Zahl versuchen, z. B. 7,2.

4. Das Quadrat von 7,2 ist 51,84. Jetzt hast du eine kleinere Zahl, die aber viel näher an 52 liegt. Wenn du mit dieser Genauigkeit zufrieden bist, kannst du die Schätzung hier beenden. Andernfalls kannst du den Vorgang mit einer Zahl zwischen 7,2 und 7,3 wiederholen, z. B. 7,22, und so weiter und so fort.

Ein anderer Ansatz ist, zuerst die Quadratwurzel zu vereinfachen und dann die Näherungswerte der Quadratzahlen zu verwenden (in der Regel auf zwei Dezimalstellen gerundet):

• Quadratwurzel aus 2: √2 ≈ 1,41,
• Quadratwurzel aus 3: √3 ≈ 1,73,
• Quadratwurzel aus 5: √5 ≈ 2,24,
• Quadratwurzel von 7: √7 ≈ 2,65,
• Quadratwurzel von 11: √11 ≈ 3,32,
• Quadratwurzel von 13: √13 ≈ 3,61,
• Quadratwurzel von 17: √17 ≈ 4,12,
• Quadratwurzel aus 19: √19 ≈ 4,34, usw.

Versuchen wir noch einmal, die Quadratwurzel von 52 zu finden. Du kannst sie zu √52 = 2√13 vereinfachen (wie man die Quadratwurzel vereinfacht, lernst du im nächsten Abschnitt) und dann √13 ≈ 3,61 einsetzen. Führe schließlich diese Multiplikation √52 ≈ 2 ∙ 3,61 = 7,22 durch. Das Ergebnis ist das gleiche wie vorher!

In manchen Situationen brauchst du den genauen Wert der Quadratwurzel nicht zu kennen. In diesem Fall ist unser Quadratwurzel-Rechner die beste Option, um den Wert von jeder gewünschten Quadratwurzel zu schätzen. Nehmen wir zum Beispiel an, du möchtest wissen, ob 4√5 größer ist als 9. Vom Rechner weißt du, dass √5 ≈ 2,23607, also 4√5 ≈ 4 × 2,23607 = 8,94428. Das ist sehr nah an 9, aber es ist nicht größer als sie! Der Quadratwurzel-Rechner liefert den Endwert mit relativ hoher Genauigkeit (auf fünf Stellen im obigen Beispiel).

Vergiss nicht, dass unser Rechner Zahlen, die in eines der Felder eingegeben werden, automatisch neu berechnet. Du kannst die Quadratwurzel einer bestimmten Zahl ermitteln, indem du das erste Fenster ausfüllst oder das Quadrat einer Zahl, die du im zweiten Fenster eingegeben hast. Die zweite Option ist praktisch, um perfekte Quadrate zu finden, die in vielen Bereichen der Mathematik und Wissenschaft wichtig sind. Wenn du zum Beispiel 17 in das zweite Feld eingibst, erfährst du, dass 289 ein perfektes Quadrat ist.

Bei einigen Anwendungen, insbesondere in den experimentellen Wissenschaften wie Chemie und Physik, werden die Ergebnisse in wissenschaftlicher Notation bevorzugt. Kurz gesagt: Eine Antwort in wissenschaftlicher Notation muss einen Dezimalpunkt zwischen den ersten beiden Zahlen haben, die nicht Null sind. Sie wird als Dezimalzahl multipliziert mit 10 und mit einem Exponenten versehen dargestellt. Zum Beispiel wird die Zahl 0,00345 als 3,45 × 10⁻³ in wissenschaftlicher Notation geschrieben, während 145,67 als 1,4567 × 10² in wissenschaftlicher Notation geschrieben wird. Die mit dem Quadratwurzel-Rechner erzielten Ergebnisse können mit dem Rechner für wissenschaftliche Notation in wissenschaftliche Notation umgewandelt werden.

Dieselbe Zahl kann oft auf mehrere Arten als Quadratwurzel dargestellt werden. Zum Beispiel: √8 = 2√2 und √9 = 3. Natürlich ist es viel einfacher, 3 als 3 zu schreiben, als sie als √9 darzustellen. Wir dehnen diese Idee auf andere Wurzeln aus - wir halten eine Form einer Wurzel für einfacher, wenn der Radikand (die Zahl unter der Wurzel) so klein wie möglich ist. Nach dieser Logik neigen wir dazu, 2√2 als "einfacheren" Ausdruck zu betrachten als √8, obwohl beide Zahlen gleich groß sind.

Eine Wurzel √x zu "vereinfachen" bedeutet also, sie in der Form a√b zu schreiben, wobei a und b ganze Zahlen sind und b so klein wie möglich ist. Das Vereinfachen von Wurzeln wird dir beim Addieren und Subtrahieren von Wurzeln nützlich sein - mehr dazu im nächsten Abschnitt!

Aber warum genau sind √8 und 2√2 die gleichen Zahlen? Das liegt daran, dass Wurzeln die Eigenschaft erfüllen:

√(x × y) = √x × √y

Mit anderen Worten: Wenn du zwei Zahlen zuerst multiplizierst und dann ihre Wurzeln nimmst, erhältst du das gleiche Ergebnis wie wenn du zuerst die Wurzeln nimmst und sie dann multiplizierst. Um dich davon zu überzeugen, dass diese nützliche Identität gilt, quadriere einfach beide Seiten und stelle fest, dass sowohl √(x × y) als auch √x × √y nicht-negative Quadratwurzeln von x × y sind. Dann erinnerst du dich daran, dass eine Zahl höchstens eine nichtnegative Quadratwurzel haben kann, und deshalb müssen √(x × y) und √x × √y gleich sein!

Mit dieser praktischen Formel können wir zeigen, dass dies tatsächlich der Fall ist:

√8 = √(4 × 2) = √4 × √2 = 2√2

Wann kannst du eine Wurzel vereinfachen? Um diese Frage zu beantworten, müssen wir die Faktoren des Radikanden finden. Nehmen wir an, der Radikand hat einen perfekten quadratischen Faktor, also 4, 9, 16, 25, 36, 49, 64 usw. (diese Zahlen können jeweils als 2², 3², 4², 5², 6², 7² ausgedrückt werden, daher der Name). Dann kannst du die Quadratwurzel vereinfachen, indem du diese Schritte befolgst:

1. Schreibe den Radikanden als Produkt aus einem perfekten Quadrat und einer anderen Zahl auf: In unserem Fall wäre das 8 = 4 × 2, weil 4 = 2² ein perfektes Quadrat ist.
2. Verwende die praktische Identität oben, um eine Wurzel des Produkts als Produkt von Wurzeln auszudrücken: √(4 × 2) = √4 × √2.
3. Ziehe die Quadratwurzel aus dem perfekten Quadrat: √4 = 2.

Wenn wir diese Schritte kombinieren, erhalten wir √8 = 2√2, wie wir es möchten! Schauen wir uns weitere Beispiele an:

• Kannst du √27 vereinfachen? Die Faktoren von 27 sind 1, 3, 9, 27. Hier gibt es eine 9, die ein perfektes Quadrat ist! Das bedeutet, dass du √27 vereinfachen kannst. Wie sieht diese Wurzel in der vereinfachten Form aus?

• Wie wäre es mit √15? Die Faktoren von 15 sind 1, 3, 5 und 15. Keiner von ihnen ist ein perfektes Quadrat, also kann diese Quadratwurzel nicht vereinfacht werden.

Was ist die wichtigste Erkenntnis aus dieser Diskussion? Du kannst eine Quadratwurzel genau dann vereinfachen, wenn sie ein perfektes Quadrat unter ihren Faktoren enthält.

Lass uns das Vereinfachen von Quadratwurzeln anhand einiger weiterer Beispiele üben:

• Wie vereinfache ich die Quadratwurzel aus 27?

  √27 = √(9 × 3) = √9 × √3 = 3√3

• Wie kann man die Quadratwurzel aus 45 vereinfachen?

  √45 = √(9 × 5) = √9 × √5 = 3√5

• Wie kann man die Quadratwurzel aus 144 vereinfachen?

  √144 = √(4 × 36) = √4 × √36 = 2 × 6 = 12

Beachte, dass du im letzten Beispiel den Faktor 144 nicht in 4 und 36 auflösen musst. Wenn du dir merkst, dass 144 = 12 × 12 ein perfektes Quadrat ist, kannst du √144 direkt zu 12 vereinfachen. Wenn du dich aber nicht spontan an große perfekte Quadrate erinnerst, ist es am einfachsten, kleine perfekte Quadrate unter den Faktoren von 144 zu identifizieren (wie wir es getan haben, indem wir gezeigt haben, dass 4 144 teilt) und 144 zuerst in kleinere perfekte Quadrate zu faktorisieren.

Was ist mit Wurzeln höheren Grades, z.B. einer [Kubikwurzel](calc: 298)? Sie können ähnlich wie Quadratwurzeln vereinfacht werden. Der Hauptunterschied besteht darin, dass du zur Vereinfachung einer Kubikwurzel mindestens einen Faktor finden musst, der ein perfekter Würfel und kein perfektes Quadrat ist, d.h. 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ und so weiter. Dann gehst du analog vor und beginnst damit, deine Zahl in einen perfekten Würfel und eine andere Zahl zu faktorisieren. Zum Beispiel kann ³√192 wie folgt vereinfacht werden:

∛192 = ∛(64 × 3) = ∛64 × ∛3 = 4∛3

Das Vereinfachen von Kubikwurzeln mag auf den ersten Blick etwas kompliziert erscheinen, aber nach einiger Übung wirst du in der Lage sein, die Wurzeln im Kopf zu vereinfachen. Vertrau uns!

Addieren und Subtrahieren von Quadratwurzeln

Leider ist das Addieren und Subtrahieren von Quadratwurzeln nicht so einfach wie das Addieren/Subtrahieren von normalen Zahlen. Wenn zum Beispiel 2 + 3 = 5 ist, bedeutet das nicht, dass √2 + √3 gleich √5 ist. Das ist falsch! Um zu verstehen, warum das so ist, stell dir vor, dass du zwei verschiedene Arten von Formen hast: Dreiecke 🔺 und Kreise 🔵. Was passiert, wenn du ein Dreieck zu einem Kreis 🔺 + 🔵 addierst? Nichts! Du hast immer noch ein Dreieck und einen Kreis 🔺 + 🔵. Was passiert aber, wenn du versuchst, drei Dreiecke zu fünf Dreiecken zu addieren? 3🔺 + 5🔺? Am Ende erhältst du acht Dreiecke 8🔺.

Das Addieren von Quadratwurzeln ist dem sehr ähnlich. Das Ergebnis der Addition von √2 + √3 ist immer noch √2 + √3. Du kannst es nicht weiter vereinfachen. Anders ist es, wenn beide Quadratwurzeln die gleiche Zahl unter dem Wurzelzeichen haben. Dann können wir sie genauso addieren, wie wir vorher Dreiecke addiert haben. Zum Beispiel: 3√2 + 5√2 ist gleich 8√2. Dasselbe gilt für das Subtrahieren von Quadratwurzeln: 3√2 - 5√2 ist gleich -2√2. Schauen wir uns weitere Beispiele an, die diese Eigenschaft der Quadratwurzel veranschaulichen:

• Was ist 6√17 + 5√17? Antwort: 6√17 + 5√17 = 11√17;

• Wie viel ist 4√7 - 7√7? Antwort: 4√7 - 7√7 = -3√7;

• Was ist 2√2 + 3√8? Antwort: 2√2 + 3√8 = 2√2 + 6√2 = 8√2, denn wir haben √8 = √(4 × 2) = √4 × √2 = 2√2 vereinfacht;

• Wie viel ist √45 - √20? Antwort: √45 - √20 = 3√5 - 2√5 = √5, denn wir haben √45 = √(9 × 5) = √9 × √5 = 3√5 und √20 = √(4 × 5) = √4 × √5 = 2√5 vereinfacht;

• Was ist 7√13 + 2√22? Antwort: 7√13 + 2√22, wir können das nicht weiter vereinfachen;

• Wie viel ist √3 - √18? Antwort: √3 - √18 = √3 - 3√2, wir können dies nicht weiter vereinfachen, aber wir haben zumindest √18 = √(9 × 2) = √9 × √2 = 3√2 vereinfacht.

Multiplizieren und Dividieren von Quadratwurzeln

Wenn das Addieren von Quadratwurzeln für dich ein Kinderspiel ist, lass uns einen Schritt weiter gehen. Was ist mit dem Multiplizieren von Quadratwurzeln und dem Dividieren von Quadratwurzeln? Hab keine Angst! Das hast du ja schon in der Lektion über das Vereinfachen von Quadratwurzeln gemacht. Das Multiplizieren von Quadratwurzeln ist dasselbe wie das Ziehen der Quadratwurzel aus dem Produkt:

√(x × y) = √x × √y

Woher das kommt, haben wir im Abschnitt über das Vereinfachen von Quadratwurzeln erklärt. Hier werden wir diese Identität aus einem anderen Blickwinkel begründen. Erinnere dich an die Quadratwurzel-Eigenschaft, die wir bereits mehrfach verwendet haben:

√x = x^1/2

Weißt du noch, wie man Zahlen multipliziert, die mit der gleichen Potenz erhöht werden? Zur Erinnerung:

xⁿ × yⁿ = (x × y)ⁿ

Wenn wir n = 1/2 nehmen, sehen wir, dass:

x^1/2 × y^1/2 = (x × y)^1/2

was eine alternative Formulierung ist für

√x × √y = √(x × y)!

Im Gegensatz zur Addition kannst du jedes Quadratwurzelpaar multiplizieren. Denke daran, dass die Multiplikation kommutativ ist: Dieses schicke Wort bedeutet, dass Zahlen in beliebiger Reihenfolge multipliziert werden können. Hier sehen wir, wie wir diese Tatsache nutzen:

• Was ist √3 × √2? Antwort: √3 × √2 = √6.

• Wie viel ist 2√5 × 5√3? Antwort: 2√5 × 5√3 = 2 × 5 × √5 × √3 = 10√15, denn die Multiplikation ist kommutativ.

• Was ist 2√6 × 3√3? Antwort: 2√6 × 3√3 = 2 × 3 × √6 × √3 = 6√18 = 18√2, wir vereinfachen √18 = √(9 × 2) = √9 × √2 = 3√2.

Wie sieht es mit dem Dividieren von Quadratwurzeln aus? Du hast Glück; die Division von Wurzeln erfüllt eine ähnliche Formel wie die Multiplikation:

√x / √y = √(x / y)

Alles, was du tun musst, ist, das Multiplikationszeichen durch eine Division zu ersetzen. Mit anderen Worten: Es ist egal, ob wir zuerst dividieren oder zuerst die Wurzeln ziehen, das Endergebnis ist dasselbe. Genau wie bei der Multiplikation ist dies ein Spezialfall (mit n = 1/2) der Formel für die Division von Potenzen:

xⁿ / yⁿ = (x / y)ⁿ

Die Division ist jedoch nicht kommutativ! Du musst die Zahlen, die vor den Quadratwurzeln stehen, und die Zahlen unter den Quadratwurzeln separat berechnen. Wie immer findest du hier einige praktische Beispiele:

• Wie viel ist √15 / √3? Antwort: √15 / √3 = √5.

• Wie viel ist 10√6 / 5√2? Antwort: 10√6 / 5√2 = (10 / 5) × (√6 / √2) = 2√3;

• Was ist 6√2 / 3√5? Antwort: 6√2 / 3√5 = (6 / 3) × (√2 / √5) = 2√(2/5).

  In dieser Form sieht die Antwort ein bisschen seltsam aus: Normalerweise bevorzugen wir eine ganze Zahl als Radikand. Das lässt sich mit ein paar weiteren Geraden Berechnungen erreichen: 2√(2/5) = (2/5) × (5√(2/5)) = (2/5) × (√(25 × 2/5)) = (2/5) √10. In Worten: Das Ergebnis ist zwei Fünftel der Quadratwurzel aus 10.

Die Berechnung der Quadratwurzel eines Exponenten oder Bruches ist dir vielleicht nicht klar. Aber mit dem Wissen, das du im vorherigen Abschnitt erworben hast, sollte es dir leichter fallen als erwartet! Beginnen wir mit den Quadratwurzeln der Exponenten. In diesem Fall wird es dir leichter fallen, die alternative Form der Quadratwurzel √x = x^^(1/2) zu verwenden. Erinnerst du dich an die Potenzregel? Wenn nicht, hier ist eine kurze Erinnerung:

(xⁿ)^m = x^{(n ∙ m)},

wobei n und m beliebige reelle Zahlen sind. Wenn du nun 1/2 anstelle von m einsetzt, erhältst du nichts anderes als eine Quadratwurzel:

√(xⁿ) = (xⁿ)^(1/2) = x^(n/2),

und so berechnet man die Quadratwurzel aus einem Exponenten. Apropos Exponenten: Die obige Gleichung sieht der Dichtefunktion der Normalverteilung sehr ähnlich, die in der Statistik häufig verwendet wird.

Wenn du dir immer noch nicht sicher bist, wie du die Quadratwurzeln aus Exponenten ziehen kannst, findest du hier ein paar Beispiele:

• Quadratwurzel aus 2⁴:

  √(2⁴) = (2⁴)^(1/2) = 2^(4/2) = 2² = 4;

• Quadratwurzel aus 5³:

√(5³) = (5³)^(1/2) = 5^(3/2); und

• Quadratwurzel aus 4⁵:

  √(4⁵) = (4⁵)^(1/2) = 4^(5/2) = (2²)^(5/2) = 2⁵ = 32.

Wie du siehst, ist es manchmal unmöglich, ein so schönes Ergebnis wie im ersten Beispiel zu erhalten. Im dritten Beispiel haben wir dir jedoch einen kleinen Trick gezeigt, indem wir 4 als 2² ausgedrückt haben. Dieser Ansatz kann kompliziertere Gleichungen oft vereinfachen.

Was ist mit Quadratwurzeln aus Brüchen? Sieh dir den vorherigen Abschnitt an, in dem wir über das Dividieren von Quadratwurzeln geschrieben haben. Dort findest du die folgende Beziehung, die alles erklären sollte:

(x / y)^(1/2) ⟺ √x / √y = √(x / y),

wobei x / y ein Bruch ist. Nachfolgend findest du einige Beispiele für Quadratwurzeln eines Bruchs:

• Quadratwurzel aus 4/9:

  √(4/9) = √4 / √9 = 2/3;

• Quadratwurzel aus 1/100:

  √(1/100) = √1 / √100 = 1/10; und

• Quadratwurzel aus 1/5:

  √(1/5) = √1 / √5 = 1/√5 = √5/5.

Die Wurzeln im Nenner zu lassen, ist keine gute Angewohnheit. Deshalb sind wir sie im letzten Beispiel losgeworden. Wir haben einfach Zähler und Nenner mit der gleichen Zahl multipliziert (das können wir immer tun, da die Zahl, mit der wir multiplizieren, gleich 1 ist), in diesem Fall mit √5.

Funktionen spielen nicht nur in der Mathematik eine wichtige Rolle, sondern auch in vielen anderen Flächeninhalten wie Physik, Statistik oder Finanzen. Die Funktion f(x) ist nichts anderes als eine Formel, die angibt, wie sich der Wert von f(x) mit dem Argument x verändert. Unten findest du den Graphen der Quadratwurzelfunktion f(x) = √x, der aus einer Hälfte der Parabel besteht. Überprüfe sie und versuche z.B. festzustellen, ob die Quadratwurzelfunktion von x = 9 3 und von x = 16 4 ist (wie sie sein sollte).

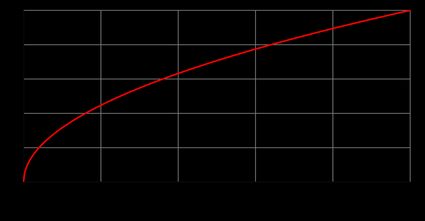
Kehren wir zur Quadratwurzelfunktion f(x) = √x zurück und untersuchen ihre grundlegenden Eigenschaften. Wir betrachten dabei nur den positiven Teil von f(x) (wie du im Quadratwurzel-Diagramm oben sehen kannst). Also die Quadratwurzelfunktion:

• Ist stetig und wachsend für alle nicht-negativen x;

• Ist differenzierbar für alle positiven x (weitere Informationen findest du im Abschnitt Ableitung der Quadratwurzel);

• Geht ins Unendliche, wenn x ins Unendliche geht (lim √x → ∞ wenn x → ∞); und

• Ist eine reelle Zahl für alle nicht-negativen x.

Die Ableitung einer Funktion sagt uns, wie schnell sich diese Funktion mit ihrem Argument ändert. Eines der einfachsten Beispiele in der Physik ist die Position eines Objekts und seine Geschwindigkeit (die Veränderungsrate der Position). Nehmen wir an, dass die Funktion x(t) beschreibt, wie sich die Entfernung des fahrenden Autos von einem bestimmten Punkt mit der Zeit t ändert. Weißt du, was bestimmt, wie schnell sich die zurückgelegte Entfernung ändert? Die Antwort ist die Geschwindigkeit des Autos! Die Ableitung der Position x(t) ist also die Geschwindigkeit v(t) (die Geschwindigkeit kann auch von der Zeit abhängen). Um die Ableitung zu bezeichnen, verwenden wir normalerweise das Hochkomma v(t) = x'(t) oder das Ableitungssymbol v(t) = dx(t)/dt.

Die Ableitung einer allgemeinen Funktion f(x) ist nicht immer einfach zu berechnen. Für einige spezielle Funktionen gibt es jedoch einige schöne Formeln. Zum Beispiel, wenn

f(x) = xⁿ

wobei n eine beliebige reelle Zahl ist, lautet die Ableitung wie folgt:

f'(x) = n × x^(n-1)

Es sieht vielleicht nicht so aus, aber das beantwortet die Frage Was ist die Ableitung einer Quadratwurzel. Erinnerst du dich an die alternative (exponentielle) Form einer Quadratwurzel? Wir wollen dich daran erinnern:

√x = x^1/2

Du siehst, dass in diesem Fall n = 1/2, also die Ableitung einer Quadratwurzel ist:

(√x)' = (x^1/2)' = 1/2 × x^-1/2 = 1/(2√x)

Da eine negative Potenz einer Zahl eine Potenz über dieser Zahl ist, muss die Ableitung mit Brüchen geschätzt werden. Wir haben ein Werkzeug, das beim Addieren oder Subtrahieren von Brüchen mit unterschiedlichen Nennern unverzichtbar sein kann. Es heißt LCM-Rechner 🇺🇸 und sagt dir, wie du das kleinste gemeinsame Vielfache findest.

Die Ableitung einer Quadratwurzel wird benötigt, um die Koeffizienten in der sogenannten Taylor-Erweiterung zu erhalten. Wir möchten nicht zu tief in die Details eintauchen, deshalb kurz: Die Taylor-Reihe ermöglicht es dir, verschiedene Funktionen** mit den Polynomen, die viel einfacher zu berechnen sind, zu annähern. Zum Beispiel ist die Taylor-Erweiterung von √(1 + x) um den Punkt x = 0 gegeben durch:

√(1 + x) = 1 + 1/2 × x - 1/8 × x² + 1/16 × x³ - 5/128 × x⁴ + ...

was für -1 ≤ x ≤ 1 gültig ist. Obwohl der obige Ausdruck unendlich viele Terme hat, kannst du nur die ersten paar Terme verwenden, um den ungefähren Wert zu erhalten. Probieren wir es aus! Mit x = 0,5 und den ersten fünf Termen erhältst du:

√(1.5) = 1 + 1/2 × 0.5 - 1/8 × 0.25 + 1/16 × 0.125 - 5/128 × 0.0625

√(1.5) ≈ 1.2241

und der echte Wert, den unser Rechner liefert, ist √(1,5) ≈ 1,2247. Das ist nah genug!

Das war bisher eine Menge Mathe und Gleichungen. Für diejenigen unter euch, die hartnäckig genug sind, haben wir den nächsten Abschnitt vorbereitet, in dem erklärt wird, wie man die Quadratwurzel einer negativen Zahl berechnet.

In der Schule hat man dir wahrscheinlich beigebracht, dass es die Quadratwurzel aus einer negativen Zahl nicht gibt. Das ist wahr, wenn du nur reelle Zahlen betrachtest. Um fortgeschrittene Berechnungen durchführen zu können, mussten die Mathematiker vor langer Zeit ein allgemeineres Set von Zahlen einführen - die komplexen Zahlen. Sie lassen sich in der folgenden Form ausdrücken:

x = a + b i

dabei ist x die komplexe Zahl mit dem Realteil a und dem Imaginärteil b. Der Unterschied zwischen einer komplexen und einer reellen Zahl ist die imaginäre Zahl i. Hier hast du einige Beispiele für komplexe Zahlen: 2 + 3i, 5i, 1,5 + 4i, und 2. Du bist vielleicht überrascht, dass 2 eine reelle Zahl ist. Ja, das ist sie, aber sie ist auch eine komplexe Zahl mit b = 0. Komplexe Zahlen sind eine Verallgemeinerung der reellen Zahlen.

Bis jetzt ist die imaginäre Zahl i wahrscheinlich noch ein Rätsel für dich. Was ist sie überhaupt? Nun, auch wenn sie seltsam aussehen mag, wird sie durch die folgende Gleichung definiert:

i = √(-1)

und das ist alles, was du brauchst, um die Quadratwurzel aus jeder Zahl zu berechnen, egal ob sie positiv ist oder nicht. Schauen wir uns ein paar Beispiele an:

• Quadratwurzel aus -9: √(-9) = √(-1 × 9) = √(-1)√9 = 3i;
• Quadratwurzel aus -13: √(-13) = √(-1 × 13) = √(-1)√13 = i√13; und
• Quadratwurzel aus -49: √(-49) = √(-1 × 49) = √(-1)√49 = 7i.

Ist das nicht einfach? Dieses Problem tritt bei der Kubikwurzel nicht auf, da du die negative Zahl durch die Multiplikation von drei identischen negativen Zahlen erhalten kannst (was du bei zwei negativen Zahlen nicht kannst). Ein Beispiel:

³√(-64) = ³√[(-4)×(-4)×(-4)] = -4

Und das ist alles, was du über Quadratwurzeln wissen musst!