Entfernungsrechner
Du möchtest die Entfernung von einem Punkt zu einem anderen oder die Entfernung zwischen zwei Städten berechnen? Du fragst dich, wie die Entfernung eigentlich definiert ist? Wir haben all diese Antworten und noch mehr, einschließlich einer detaillierten Erklärung, wie du die Entfernung zwischen zwei beliebigen Objekten im zweidimensionalen Raum berechnest. Zudem sprechen wir darüber, wie wir Entfernungen unterschiedlich ausdrücken können (zum Beispiel als prozentuale Differenz). Wir sind uns sicher, dass du viel Spaß mit diesem Rechner haben wirst!
Du siehst lieber zu als zu lesen? Mit diesem Video, das wir für dich vorbereitet haben, lernst du in 90 Sekunden alles, was du wissen musst:
Was sind Entfernungen?
Bevor wir uns damit beschäftigen, wie Entfernungen berechnet werden, sollten wir klären, was eine Entfernung ist. Es ist der eindimensionale Raum zwischen zwei Punkten. Diese Definition drückt aus, was wir auch intuitiv unter Entfernung verstehen. Es ist aber nicht die einzige Möglichkeit, wie wir über Entfernung sprechen können. In den folgenden Abschnitten wirst du lernen, wie das Konzept der Entfernung über die Angabe in Länge nach Einsteins Relativitätstheorie um mehr als einen Sinn hinaus erweitert werden kann.
Wenn wir bei der geometrischen Definition von Entfernung bleiben, müssen wir immer noch definieren, in welcher Art von Raum wir uns befinden. In den meisten Fällen handelt es sich wahrscheinlich um drei Dimensionen oder weniger, da das dem Maximum unserer Vorstellungskraft entspricht. Für diesen Rechner konzentrieren wir uns auf die zweidimensionale-Distanz (mit einer Dimension als Sonderfall). Wenn du die dreidimensionalen Entfernung zwischen 2 Punkten finden möchtest, empfehlen wir dir, unseren 3D Entfernungsrechner 🇺🇸 zu verwenden, der speziell für diesen Zweck entwickelt wurde.
Um die Entfernung zwischen zwei Punkten zu bestimmen, brauchst du zunächst logischerweise zwei Punkte. Diese Punkte werden durch ihre Koordinaten im Raum beschrieben. Jeden Punkt im zweidimensionalen Raum wird durch zwei, für diesen Punkt eindeutige, Koordinaten, angegeben. Du kannst diesen Rechner auch verwenden, um die Entfernung zwischen zwei Punkten im eindimensionalen
Raum zu ermitteln, indem du einfach für beide Punkte die gleichen Koordinaten verwendest. Da dies ein sehr spezieller Fall ist, werden wir ihn nicht weiter berücksichtigen und von nun an nur noch über Entfernungen in zwei Dimensionen sprechen.

Um mathematisch genau und präzise zu sein, definieren wir im nächsten Schritt die Art des Raums, in dem wir rechnen. Nein, warte, lauf nicht weg! Es ist einfacher, als du denkst. Wenn du nicht weißt, in welcher Art Raum du arbeitest, oder du nicht einmal wusstest, dass es mehr als eine Art von Raum gibt, arbeitest du höchstwahrscheinlich im euklidischen Raum. Das ist der „Standard”-Raum, in dem wir fast alle geometrischen Operationen durchführen und mit welchem auch der Rechner arbeitet. Lass uns genauer anschauen, was der euklidische Raum ist, welche Eigenschaften er hat und warum er so wichtig ist.
Die Formel für die euklidische Entfernung
Der euklidische Raum oder Anschauungsraum ist ganz einfach gesagt die Beschreibung eines normalen zweidimensionalen Raums. Im euklidischen Raum beträgt die Summe der Winkel eines Dreiecks gleich 180º und alle Winkel von Quadraten sind gleich 90º – immer. Auch wenn wir das für selbstverständlich halten, ist das nicht in allen Räumen der Fall. Verwechsle den euklidischen Raum nicht mit mehrdimensionalen Räumen. Der euklidische Raum kann so viele Dimensionen haben, wie sie in endlicher Anzahl vorkommen können und die Regeln des euklidischen Raums befolgen.
Wir möchten dich nicht mit mathematischen Definitionen darüber, was ein Raum ist und was den euklidischen Raum einzigartig macht, langweilen. Das wäre auch ein zu komplexes Thema für sich, um es in einem einfachen Entfernungsrechner zu erklären. Wir werden dir jedoch einige Beispiele für andere, häufig verwendete Räume zeigen, die dir dabei helfen werden zu verstehen, warum der euklidische Raum nicht der einzige Raum ist. Zudem wird dir hoffentlich klar sein, warum wir uns nicht die Mühe machen, Entfernungen in anderen Räumen zu berechnen.

Das erste Beispiel eines anderen Raums ist ein wenig merkwürdig, aber eine sehr wichtige Art von Raum: der vierdimensionale Minkowski-Raum. Wir haben ihn ausgewählt, weil er in der Physik sehr verbreitet ist und insbesondere in der Relativitätstheorie, der allgemeinen Relativitätstheorie und sogar in der relativistischen Quantenfeldtheorie verwendet wird. Dieser Raum ist dem euklidischen Raum sehr ähnlich, unterscheidet sich aber in einem ganz entscheidenden Punkt von ihm: der Addition des Skalarprodukts, auch inneres Produkt genannt (nicht zu verwechseln mit dem Kreuzprodukt).
Sowohl der euklidische als auch der Minkowski-Raum sind das, was Mathematiker als flachen Raum bezeichnen. Das bedeutet, dass der Raum selbst flache Eigenschaften hat: zum Beispiel ist die kürzeste Entfernung zwischen zwei beliebigen Punkten immer eine gerade Linie zwischen ihnen (siehe lineare Interpolation Rechner 🇺🇸). Es gibt jedoch auch andere Arten von mathematischen Räumen, die gekrümmte Räume genannt werden. In ihnen ist der Raum von Natur aus gekrümmt und die kürzeste Entfernung zwischen zwei Punkten ist keine gerade Linie.
Dieser gekrümmte Raum ist in drei Dimensionen schwer vorstellbar. Für zwei Dimensionen können wir uns aber vorstellen, dass wir statt einer flachen, ebenen Fläche einen zweidimensionalen Raum haben, der zum Beispiel in Form der Oberfläche einer Kugel gekrümmt ist. In diesem Fall passieren sehr seltsame Dinge. Die kürzeste Entfernung von einem Punkt zu einem anderen ist keine gerade Linie, da aufgrund der Krümmung des Raums keine Linie gerade ist. Eine weitere merkwürdige Eigenschaft dieses Raums ist, dass sich einige parallele Linien 🇺🇸 wirklich in einem Punkt treffen. Um dieses Konzept besser zu verstehen, kannst du an die vertikalen Längengrade denken, die die Erde in viele Zeitzonen unterteilen und sich an den Polen kreuzen.
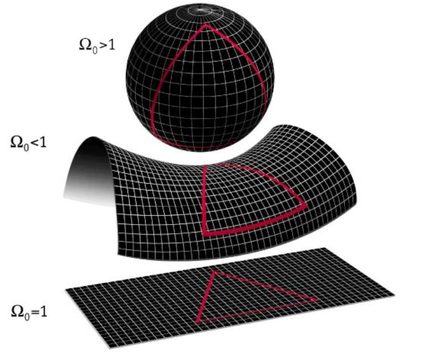
Es ist wichtig zu beachten, dass Koordinaten des beispielsweise euklidischen Raums nicht einfach umgewandelt werden können, um sie im gekrümmten Raum angeben zu können, da dieser sich im Konzept unterscheidet. Wenn wir die Standardkoordinaten nehmen und sie in polare, zylindrische oder sogar sphärische Koordinaten umwandeln, befinden wir uns immer noch im euklidischen Raum. Wenn wir vom gekrümmten Raum sprechen, meinen wir, was die Eigenschaften betrifft, einen ganz anderen Raum. In sphärischen Koordinaten existieren noch gerade Linie und Entfernungen werden immer noch in Geraden gemessen, auch wenn sich das nur sehr schwer in Zahlen ausdrücken lässt.
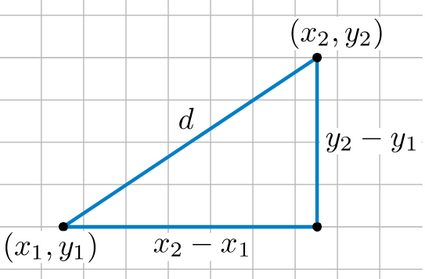
Kehren wir zum euklidischen Raum zurück, um dir jetzt die Entfernungsformel vorzustellen, die wir am Anfang versprochen haben. Sie lautet:
Sie basiert auf dem Satz des Pythagoras, welcher besagt, dass ist. Hier sind und die Schenkel eines rechtwinkligen Dreiecks und ist die Hypotenuse. Nehmen wir an, dass zwei Punkte, und , die Koordinaten der Endpunkte der Hypotenuse sind. Dann entspricht in der Entfernungsgleichung und entspricht . Da ist, kannst du sehen, dass dies nur die Anwendung des Satzes des Pythagoras ist.
Entfernung zu geschlossenen Objekten
Die obige Formel ist die standardmäßige euklidische Entfernungsformel. Wenn du aber weiter darüber nachdenkst, kann sie ein wenig begrenzt erscheinen. Oft möchten wir nicht nur die Entfernung zwischen zwei Punkten ermitteln. Manchmal möchten wir die Entfernung von einem Punkt zu einer Linie oder zu einem Kreis berechnen. In diesen Fällen müssen wir zuerst festlegen, welchen Punkt auf der Linie oder dem Kreis wir für die Entfernungsberechnung verwenden möchten, und dann die obige Formel anwenden.
Hier spielt das Konzept der Senkrechten 🇺🇸 eine Rolle. Die Entfernung zwischen einem Punkt und einem geschlossenen Objekt wird über die Senkrechte definiert. Aus geometrischer Sicht besteht der erste Schritt zur Messung der Entfernung von einem Punkt zu einem anderen darin, eine Gerade zwischen beiden Punkten zu zeichnen und dann die Länge dieser Gerade zu messen. Wenn wir die Entfernung zwischen einem Punkt und einer Gerade messen, stellt sich natürlich die Frage: „Welche der vielen möglichen Geraden soll ich ziehen?”. In diesem Fall lautet die Antwort: die Gerade von dem Punkt, die senkrecht zur ersten Gerade steht. Dort, wo der Punkt ein Teil der Gerade ist, ist diese Entfernung gleich null. Für diese eindimensionalen Fälle können wir nur die Entfernung zwischen den Punkten berücksichtigen, weil die Gerade den gesamten eindimensionalen Raum darstellt.
Dadurch entstehen Einschränkungen bei der Berechnung von Entfernungen in einigen interessanten geometrischen Fällen. Wir könnten zum Beispiel das Konzept der Höhe eines Dreiecks umdefinieren, sodass sie einfach die Entfernung zwischen einem Scheitelpunkt und der gegenüberliegenden Seite des Dreiecks ist. In diesem Fall wird auch die Fläche des Dreiecks in Bezug auf die Entfernung neu definiert, da sie eine Funktion der Höhe des Dreiecks ist.
Entfernung zu einer Geraden und zwischen 2 Geraden
Schauen wir uns ein paar Beispiele im zweidimensionalen Raum an. Um die Entfernung zwischen einem Punkt und einer Geraden zu berechnen, könnten wir vorgehen (das Segment senkrecht zur Gerade von der Gerade zum Punkt berechnen und dann seine Länge berechnen) oder wir könnten :
wobei die Gerade durch und der Punkt durch definiert ist.
Das einzige Problem dabei ist, dass eine Gerade in der Regel mit angegeben wird, sodass wir diese Gleichung in die zuvor gezeigte Form umwandeln müssen:
wir können also sehen, dass , und ist. Damit ergibt sich aus der vorherigen Gleichung folgendes:
Um die Entfernung zwischen zwei Geraden zu bestimmen, müssen wir nur die Länge des Abschnitts berechnen, der von der einen zur anderen Gerade geht und senkrecht zu beiden steht. Auch hierfür gibt es eine :
wenn die Geraden und sind. Wir können diesen Ausdruck auch in die Geradengleichung umwandeln und folgendes erhalten:
für die Zeilen und .
Beachte, dass beide Geraden parallel sein müssen, da sie sich sonst an irgendeinem Punkt berühren würden und ihre Entfernung dann wäre. Da für parallele Geraden und gilt, werden die tiefgestellten Buchstaben in den Formeln meistens weglassen, während die parallelen Geraden in der Geradengleichung mit dargestellt werden.
So findest du die Entfernung mit unserem Entfernungsrechner
Wie wir bereits erwähnt haben, kann die Entfernung vieles bedeuten. Deshalb haben wir in diesem Rechner ein paar verschiedene Optionen für dich bereitgestellt. Du kannst die Entfernung zwischen einem Punkt und einer Geraden, die Entfernung zwischen zwei Geraden (sie müssen immer parallel sein) oder die Entfernung zwischen Punkten im Raum berechnen. Wenn du die Entfernung zwischen zwei Punkten berechnen möchtest, hast du die Möglichkeit, dies in 1, 2, 3 oder 4 Dimensionen zu tun. Wir wissen, 4 Dimensionen klingen gruselig, du musst diese Option auch nicht sofort nutzen. Du kannst jederzeit mehr darüber lernen, indem du liest und mit dem Rechner herumexperimentierst. Wir versprechen, dass weder das Internet noch das Universum daran zerbrechen werden.
Du kannst mit dem Rechner auch 3 verschiedene Punkte im Raum definieren, von denen du dann die 3 Paare der Entfernungen zwischen ihnen erhältst. Das spart Zeit, wenn du mehr als zwei Koordinatenpunkte hast. Die Anzahl der Dimensionen, in denen du rechnest, bestimmt die Anzahl der Koordinaten, die einen Punkt beschreiben. Wenn du die Anzahl der Dimensionen erhöhst, fragt dich der Rechner auch nach mehr Eingabewerten.
Auch wenn die Verwendung des Rechners sehr einfach ist, haben wir uns entschieden, dir einen Schritt-für-Schritt-Lösungsweg für die Berechnung zu zeigen. So kannst du dich mit der Entfernungsformel und ihrer Anwendung vertraut machen. Schauen wir uns nun ein praktisches Beispiel an: Wie findest du die Entfernung zwischen zwei Punkten im zweidimensionalen Raum.
Angenommen, du hast zwei Koordinaten, und , und möchtest die Entfernung zwischen ihnen berechnen. Um die zweidimensionale Entfernung zwischen diesen beiden Punkten zu berechnen, befolge diese Schritte:
- Setze die Werte in die Formel ein: .
- Subtrahiere in der Formel die Werte in den Klammern.
- Quadriere beide Mengen in den Klammern.
- Addiere die Ergebnisse.
- Ziehe die Quadratwurzel.
- Verwende den Entfernungsrechner, um dein Ergebnis zu überprüfen.
Wenn du das Beispiel handschriftlich nachrechnest, erhältst du:
was ungefähr entspricht. Beachte, dass du beim Ziehen der Quadratwurzel ein positives und ein negatives Ergebnis erhältst. Da es sich um eine Entfernung handelt, interessiert dich nur das positive Ergebnis. Der Rechner geht diese Berechnungen Schritt für Schritt durch und gibt dir das Ergebnis in genauer und ungefährer Form an.
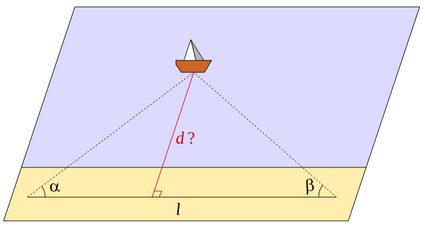
Fahrstrecke zwischen Städten: ein Praxisbeispiel
Werfen wir einen Blick auf eine der Anwendungen des Entfernungsrechners. Angenommen, du fährst von Stadt A nach Stadt B mit einem Zwischenstopp in Stadt C, wobei die Route von A nach B senkrecht zur Route von B nach C verläuft. Wir können die Entfernung von A nach B bestimmen und dann, wenn wir den Benzinpreis kennen, die Kraftstoffkosten, den verbrauchten Kraftstoff und die Kosten pro Person für die Fahrt ermitteln. Bei der Berechnung des Kraftstoffes könnte dir auch Omni's Kraftstoffrechner behilflich sein.
Die Schwierigkeit dabei ist, die Entfernungen zwischen den Städten ganz genau zu berechnen. Eine Gerade (wie die, die wir in diesem Rechner verwenden) kann eine gute Annäherung sein. Sie kann aber ziemlich daneben liegen, wenn die Route, die du nimmst, nicht komplett gerade ist, sondern Umwege hat, z. B. wenn du Berge umfahren oder durch eine andere Stadt musst. In diesem Fall ist es besser, Google Maps oder ein anderes Tool zu verwenden, das die Entfernung entlang eines Weges berechnet und nicht nur die Entfernung von einem Punkt zum anderen als Luftlinie.

Unser Rechner kann richtige Messungen und Vorhersagen für Entfernungen zwischen Objekten machen, aber nicht für die Länge eines Weges. Trotzdem gibt es verschiedene Szenarien, in denen du dich für die Entfernung zwischen Objekten interessierst, unabhängig von der Länge des Weges, den du nehmen musst. Ein solches Beispiel ist die Entfernung zwischen astronomischen Objekten.
Entfernung von der Erde zum Mond und zu der Sonne — astronomische Entfernungen
Wenn wir eine Entfernung auf unserer Erde betrachten, kommen wir oft nicht weit, ohne auf einige Probleme zu stoßen. Angefangen bei der Krümmung des Raums (weil die Erdkrümmung nicht Null ist) bis hin zur begrenzten maximalen Entfernung zwischen zwei Punkten auf der Erde. Aus diesem Grund und auch weil es Universen jenseits unserer Erde gibt, sind Entfernungen im Universum für viele Menschen von großem Interesse. Da wir bisher noch keine geeigneten Reisemittel für interplanetare Reisen entwickelt haben, geschweige denn für interstellare Reisen, konzentrieren wir uns vorerst auf die tatsächliche euklidische Entfernung zu einigen Himmelsobjekten. Zum Beispiel die Entfernung zwischen der Erde und der Sonne oder die Entfernung zwischen der Erde und dem Mond.
Diese Entfernungen liegen jenseits des Vorstellungsvermögens unseres Gehirns. Es fällt uns schwer, die Größe unseres Planeten zu erfassen, geschweige denn das riesige, unendliche Universum. Es ist so schwierig sich das vorzustellen, dass wir die wissenschaftliche Notation oder Lichtjahre als Entfernungseinheit für solch große Längen verwenden müssen, um sie veranschaulichen zu können. Die längsten Reisen, die du auf der Erde unternehmen kannst, sind kaum ein paar tausend Kilometer weit, während die Entfernung von der Erde zum Mond, dem uns am nächsten gelegenen Himmelskörper, 384 000 km beträgt. Die Entfernung zu unserem nächsten Stern, also die Entfernung von der Erde zur Sonne, beträgt sogar 150 000 000 km oder etwas mehr als 8 Lichtminuten.

Wenn du diese Entfernungen mit der Entfernung zu unserem zweitnächsten Stern (Alpha Centauri) vergleichst, die 4 Lichtjahre beträgt, wirken Sterne plötzlich viel kleiner. Wenn wir noch mehr verrückte Vergleiche anstellen möchten, können wir immer an einen Flug von Berlin nach Sydney denken, der in der Regel mehr als 20 Stunden dauert und über 16 000 km beträgt, und ihn mit der Größe des beobachtbaren Universums vergleichen, die bei etwa 46 600 000 000 Lichtjahren liegt !
Hier haben wir versehentlich einen faszinierenden Punkt aufgedeckt, nämlich dass wir Entfernungen nicht nur in Länge, sondern auch in Zeit messen können. So erweitern wir den Begriff der Entfernung über seinen geometrischen Sinn hinaus. Wir werden uns diese Möglichkeit im nächsten Abschnitt genauer anschauen, wenn wir über die Bedeutung und den Nutzen von Entfernungen jenseits des rein geometrischen Sinns sprechen. Dies ist vor allem durch das philosophische Bedürfnis inspiriert, jedem Konzept eine universelle Bedeutung zu geben, sowie durch die offensichtliche physikalische Theorie, die zu erwähnen ist, wenn man über Permutationen von Raum und Zeit oder jede andere Variable, die gemessen werden kann, spricht.
Entfernung über die Länge hinaus
Normalerweise bezieht sich das Konzept der Entfernung auf den geometrischen, euklidischen Abstand und ist mit der Länge verbunden. Wenn du die Definition von Entfernung jedoch so erweiterst, dass sie allgemein den Unterschied zwischen zwei Dingen meint, eröffnet sich eine neue Welt voller Möglichkeiten. Plötzlich kannst du entscheiden, wie du die Entfernung zwischen zwei Dingen am besten misst und sie in eine möglichst nützliche Größe umwandelst. Um dies noch weiter zu vereinfachen, kannst du dir bewusst werden, dass die Entfernung zwischen zwei Zahlen nichts anderes ist als die eindimensionale Differenz zwischen diesen Zahlen. Um diesen Wert zu erhalten, subtrahieren wir die eine Zahl einfach von der anderen. Das Ergebnis ist die Differenz, auch bekannt als die Entfernung.
Wir könnten von dieser numerischen Entfernung zum Beispiel auf die Differenz oder die Entfernung in Form der prozentualen Differenz übergehen, die in manchen Fällen eine bessere Vergleichsmöglichkeit bietet. Das ist noch immer nur eine Abstraktionsebene, bei der wir einfach die Maßeinheiten weglassen. Aber was wäre, wenn wir ganz andere Einheiten verwenden würden?

Wenn wir den Sinn des Begriffes Entfernung so erweitern, dass er eine Differenz angibt, können wir den Unterschied zwischen zwei Temperaturen oder anderen Größen wie dem Druck berechnen. Wir müssen jetzt aber nicht direkt ins Extreme gehen, schauen wir uns an, wie zwei Punkte, abhängig von den getroffenen Annahmen durch eine unterschiedliche Entfernung getrennt werden können. Um auf das Beispiel mit der Fahrstrecke zurückzukommen, könnten wir die Entfernung in Zeit messen, anstatt in Länge. In diesem Fall brauchen wir eine Annahme, um eine solche Umrechnung zu ermöglichen, nämlich die Art der Beförderung.
Es gibt einen großen Unterschied zwischen der Zeit, die man braucht, um 10 km mit dem Flugzeug zurückzulegen, und der Zeit, die man dafür mit dem Auto braucht. Andererseits wird z. B. die Entfernung eines Blitzes in Zeit gemessen und dann in die Länge umgerechnet. Das bringt uns zu einem interessanten Punkt: dem Umrechnungsfaktor zwischen zeitlicher Entfernung und Länge. Wir kennen ihn als die Geschwindigkeit. Beschleunigte Bewegungen wie der freie Fall unter den Gesetzen der Schwerkraft zeigen, dass Geschwindigkeit nicht konstant sein muss. Weitere Beispiele dafür sind die Verbindung zwischen Bremszeit und Bremsweg durch die Bremskraft und den Luftwiderstand oder, in sehr extremen Fällen, durch die Kraft eines Autounfalls.

Ein weiteres Gebiet, in welchem du seltsame Entfernungseinheiten finden kannst, ist die Festkörperphysik. Hier wird die Entfernung, die ein Teilchen im Inneren eines Materials zurücklegt, oft als Durchschnitt der Wechselwirkungen oder Kollisionen ausgedrückt. Diese Entfernung wird mit der Länge verknüpft, indem die mittlere freie Weglänge verwendet wird, also die mittlere Entfernung (in Länge), die ein Teilchen zwischen den Wechselwirkungen zurücklegt. Wenn wir noch weiter gehen möchten, können wir über die Entfernung vom gegenwärtigen Wert zum zukünftigen Wert eines Autos nachdenken.
Wir möchten aber nicht, dass jemandem das Gehirn explodiert, also denk bitte nicht zu viel darüber nach. Nimm einfach diesen Rechner und verwende ihn für längenbasierte Entfernungen im zweidimensionalen Raum. Du kannst jederzeit zu dieser philosophischen Betrachtung von Entfernungen zurückkehren, wenn dir mal langweilig ist!
FAQs
Wie findet man die Entfernung zwischen zwei Punkten?
Um die Entfernung zwischen zwei Punkten zu bestimmen, verwenden wir die Entfernungsformel: √[(x₂ - x₁)² + (y₂ - y₁)²]:
- Bestimme die Koordinaten der beiden Punkte im Raum.
- Ziehe die x-Koordinaten des einen Punktes vom anderen ab und tue dasselbe für die y-Koordinaten.
- Quadriere beide Ergebnisse separat.
- Addiere die Werte, die du im vorherigen Schritt erhalten hast.
- Finde die Quadratwurzel aus dem obigen Ergebnis.
Wenn dir das zu viel Aufwand ist, kannst du auch einfach den Entfernungsrechner von Omni verwenden.
Ist die Entfernung ein Vektor?
Die Entfernung ist kein Vektor. Die Entfernung zwischen Punkten ist eine skalare Größe, d.h. sie ist nur durch ihren Wert definiert. Die Verschiebung ist jedoch ein Vektor mit Wert und Richtung. die Entfernung zwischen A und B ist also derselbe wie die Entfernung von B zu A, aber die Verschiebung ist je nach Reihenfolge der Punkte unterschiedlich.
Was ist ein Klick?
Ein Klick ist ein Kilometer oder 0,62 Meilen. Das Wort wird vor allem im amerikanischen und britischen Militär zur Bezeichnung einer Entfernung von einem Kilometer verwenden.
Wie lautet die Entfernungsformel?
Die Entfernungsformel lautet: √[(x₂ - x₁)² + (y₂ - y₁)²]. Sie funktioniert für zwei beliebige Punkte im zweidimensionalen Raum, mit den Koordinaten (x₁, y₁) für den ersten Punkt und (x₂, y₂) für den zweiten Punkt. Du kannst dir das leicht einprägen, wenn du dir merkst, dass sie auf dem Satz des Pythagoras basiert, wobei die Entfernung die Hypotenuse des Dreiecks bildet und die Längen der Katheten die Differenz zwischen den x- und y-Komponenten der Punkte darstellen.
Wie findet man die Entfernung eines Vektors?
Die Entfernung eines Vektors ist ihr Betrag. Wenn du ihre Komponenten kennst:
- Nimm jede der Komponenten des Vektors und quadriere sie.
- Addiere sie.
- Finde die Quadratwurzel aus dem vorherigen Ergebnis.
- Viel Spaß bei der Berechnung!
Wenn du die polare Darstellung des Vektors kennst, hast du eine Zahl und einen Winkel. Diese Zahl ist der Betrag des Vektors, der seine Entfernung angibt.
Was ist die SI-Einheit der Entfernung?
Die SI-Einheit des Entfernung sind Meter (m). Andere gebräuchliche Einheiten im Internationalen Einheitensystem sind unter anderem Zentimeter (ein Hundertstel eines Meters) und Kilometer (eintausend Meter).
Wie groß ist die Entfernung von A nach B?
Die Entfernung von A nach B ist die Länge der Geraden, die von A nach B führt. Die Entfernung von B nach A ist die gleiche wie die Entfernung von A nach B, weil die Entfernung ein Skalarprodukt ist.
Was ist die Dimension der Entfernung?
die Entfernung ist ein Maß für den eindimensionalen Raum. die Entfernung zwischen zwei Punkten ist die kürzeste Gerade des eindimensionalen Raums zwischen ihnen. Wenn du die Entfernung durch Zeit teilst, erhältst du die Geschwindigkeit, die die Dimensionen von Raum durch Zeit hat.
Ist Lichtjahr Zeit oder Entfernung?
Ein Lichtjahr ist ein Maß für die Entfernung. Es entspricht 9,461∙1012 Kilometern. Das ist die Strecke, die ein Lichtstrahl in einem perfekten Vakuum innerhalb eines Jahres zurücklegt.
Wie finde ich die Entfernung aus Geschwindigkeit und Zeit?
Anhand der Geschwindigkeit und der Bewegungszeit eines Objekts kannst du die Entfernung berechnen:
- Achte darauf, dass die Geschwindigkeit und die Zeit kompatible Einheiten haben (z. B. Meter pro Sekunde und Sekunden...).
- Wenn das nicht der Fall ist, rechne sie in die erforderlichen Einheiten um.
- Multipliziere die Geschwindigkeit mit der Zeit.
- Das Ergebnis ist die zurückgelegte Strecke in der Längeneinheit, die du für die Geschwindigkeit verwendet hattest!
