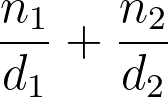Calculadora de Frações

Boas-vindas à calculadora de frações da Omni, uma ferramenta realmente versátil. Com ela, você pode:

• ➕ somar;
• ➖ subtrair;
• ✖️ multiplicar; e
• ➗ dividir duas frações quaisquer.

Além disso, ela tem a capacidade de simplificar uma fração (também conhecida como redução), bem como te ensinar como transformar uma fração em decimal e vice-versa. Se você ainda não está impressionado, essa ferramenta não só funciona com frações próprias e impróprias, mas também com frações mistas, o que mais você poderia pedir? 😁

Como de costume, preparamos algumas leituras introdutórias que permitirão que você mergulhe no mundo das frações 🌎. A seguir, você lerá sobre a definição de fração, os tipos de frações (próprias, impróprias e mistas) e todas as operações básicas com frações simples e mistas. Você está pronto?

Uma fração representa a divisão em partes iguais de uma quantidade inteira.
Você pode reconhecer uma fração simples porque ela tem dois números separados por uma linha (ou barra):

• Chamamos o número superior de numerador e o escrevemos acima da linha. Ele nos diz:

  Quantas partes nós temos.

• Chamamos o número inferior de denominador e o exibimos abaixo da linha. Ele significa:

  O número total de partes.

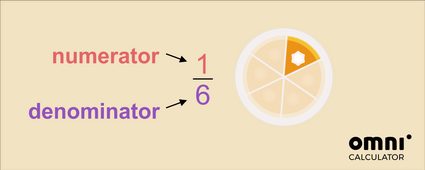
No exemplo acima, vemos uma de seis fatias, nas quais o bolo foi cortado ou dividido. Lemos isso como um sexto do bolo inteiro.

Mas, é claro, o bolo pode ser cortado de forma diferente!

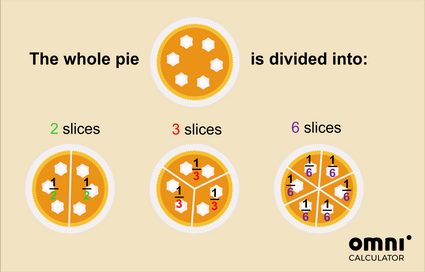
Portanto, se você cortar o bolo em duas partes, uma fatia será a metade do todo. Já, se você cortar o bolo em 3 partes, uma fatia será um terço do bolo inteiro, etc.

As frações são usadas ao nosso redor:

• Toda vez que você quiser expressar parte de um item inteiro, que pode ser dividido em partes iguais: como um bolo 🍰, uma barra de chocolate 🍫, uma melancia 🍉, uma pizza 🍕, etc;

• Quando medimos algo 📏, especialmente em milímetros:

• O tamanho da tela do seu computador 🖥️ é expresso como uma proporção, por exemplo, 16:9, que também é uma fração, ela apenas é escrita de uma forma diferente. Para obter informações sobre como simplificar as proporções, confira a calculadora de razão da Omni!

Então, agora que você conhece a definição de fração, vamos dar uma olhada nos diferentes tipos de frações. Em geral, temos três tipos de frações: frações próprias, impróprias e mistas:

1. Frações próprias

   Em frações próprias, o número superior (numerador) é menor que o número inferior (denominador). Isso significa que ele sempre será menor do que um inteiro, por exemplo, você pode considerar o seguinte exemplo:

   🍰 5 fatias de um bolo cortado em 6;

   2 fileiras de uma barra de chocolate de 5 fileiras; e

   7 partes de uma laranja que cortamos em 8.

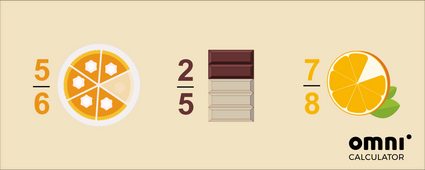
A regra geral, que funciona tanto para números positivos quanto negativos, é que o valor absoluto da fração é menor que um:

|^numerador/_denominador| < 1

2. Frações impróprias

   Então, o que é uma fração imprópria? É uma fração em que o numerador é maior do que (ou igual a) o denominador. As frações impróprias são, às vezes, chamadas de frações de peso superior. Exemplos de frações impróprias são:

   🍰 10 fatias de bolo, quando cada bolo tem 6 fatias;

   8 fileiras de uma barra de chocolate. Sendo que a barra de chocolate inteira tem 5 fileiras; e

   21 partes de laranja, se cortarmos cada laranja em 8 partes iguais.

3. Frações mistas

   As frações mistas, também conhecidas como numerais mistos ou números mistos, são outra forma de expressar uma fração imprópria. Elas são formadas pela combinação de números inteiros (o número de quantidades inteiras) e uma fração própria. Então, vamos dar uma olhada nos exemplos do parágrafo anterior:

   🍰 10 fatias de bolo, quando cada bolo tem 6 fatias é o mesmo que → 1 bolo inteiro mais 4 de 6 fatias;

   🍫 8 fileiras de chocolate quando a barra de chocolate inteira tem 5 fileiras → 1 barra de chocolate inteira mais 3 de 5 fileiras; e

   🍊 21 partes de laranja, se cortarmos a laranja em 8 fatias → 2 laranjas inteiras mais cinco de 8 fatias.

Quando se trata de somar frações, há três cenários:

1. O denominador (número inferior) é o mesmo em ambas as frações, por exemplo: ³/₅ e ¹/₅

   Esse é o caso mais simples; tudo o que você precisa fazer é somar os numeradores (números superiores) e deixar o denominador como está:

   ➽ ³/₅ + ¹/₅ = ^{(3 + 1)}/₅ = ⁴/₅

2. As frações têm denominadores diferentes, por exemplo: ²/₅ e ³/₁₀

   Esse é um caso um pouco mais complicado. Para somar essas frações, você precisa encontrar o denominador comum.

   • Você pode usar, por exemplo, o MMC (mínimo múltiplo comum), para encontrar o número comum de seus dois denominadores: MMC(5,10) = 10 Outra opção é multiplicar os denominadores e reduzir a fração posteriormente.

   • Em seguida, você precisa expandir cada fração para ter esse denominador comum como seu número inferior:

   Portanto, você deve multiplicar a fração com o denominador igual a 5 (nosso 1/5) por 2, para obter 10 (lembre-se de que você deve multiplicar os números superior e inferior):

   ➽ ²/₅ = ^{(2 × 2)}/_{(5 × 2)} = ⁴/₁₀

   Sua segunda fração já tem o denominador igual a 10:

   ➽ ³/₁₀

   • Agora que suas frações têm o mesmo denominador, você pode somá-las:

     ➽ ⁴/₁₀ + ³/₁₀ = ^{(4 + 3)}/₁₀ = ⁷/₁₀

3. Você deseja somar duas frações mistas, por exemplo: 2 ³/₅ e 1 ¹/₂

   Uma solução para esse tipo de problema é converter a fração mista em uma fração imprópria e somá-la como de costume.

   Vamos converter a fração mista 2 ³/₅

   • Multiplique o número inteiro pelo denominador:

     2 ⋅ 5 = 10

   • Adicione o resultado ao numerador:

     10 + 3 = 13

   • Esse é o seu novo numerador - escreva-o em cima do denominador:

     2 ³/₅ = ¹³/₅

   Analogamente, você pode descobrir que 1 ¹/₂ = ³/₂.

   • Faça a adição padrão de frações com denominadores desiguais:

     ➽ ¹³/₅ + ³/₂ = ²⁶/₁₀ + ¹⁵/₁₀ = ⁴¹/₁₀

   • Por fim, você pode converter o resultado novamente em uma fração mista:

     Você pode fazer uma divisão com um resto:

     ➽ ⁴¹/₁₀ = 4 R 1 = 4 ¹/₁₀

É claro que nossa calculadora de frações lida com todos esses cenários. 😎

Se você ainda estiver se perguntando como funciona a adição de frações, talvez a figura abaixo te ajude.

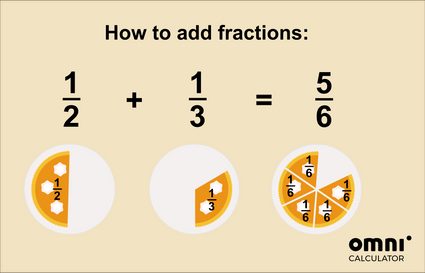
Para obter uma explicação ainda mais detalhada, consulte nossa calculadora de adição de frações 🇺🇸.

Se você está se perguntando como subtrair frações e já leu a seção anterior sobre como somar frações, temos boas notícias para você: o procedimento é praticamente o mesmo!

1. Se você tiver frações com o mesmo denominador, subtraia os numeradores:

   ➽ ³/₅ - ¹/₅ = ^{(3 - 1)}/₅ = ²/₅

2. Ao subtrair frações com denominadores diferentes (²/₅ e ³/₁₀) repita o procedimento da seção anterior, mas subtraindo ao invés de somar na etapa final:

   • Encontre um denominador comum, neste caso é 10.

   • Expanda as frações para suas frações equivalentes com um denominador comum: ⁴/₁₀ e ³/₁₀.

   • Subtraia os numeradores.

     ➽ ²/₅ - ³/₁₀ = ⁴/₁₀ - ³/₁₀ = ¹/₁₀

3. Para frações mistas (2³/₅ e 1 ¹/₂):

   • Altere as frações mistas para frações impróprias, como antes:

     2 ³/₅ = ¹³/₅ e 1 ¹/₂ = ³/₂

   • Subtraia as duas frações impróprias com denominadores desiguais:

     ➽ ¹³/₅ - ³/₂ = ²⁶/₁₀ - ¹⁵/₁₀ = ¹¹/₁₀

   • Deixe-a em uma fração imprópria ou converta-a novamente em uma fração mista:

     ➽ ¹¹/₁₀ = 1 R 1 = 1 ¹/₁₀

Você pode imaginar a subtração como tirar ou comer parte do bolo:

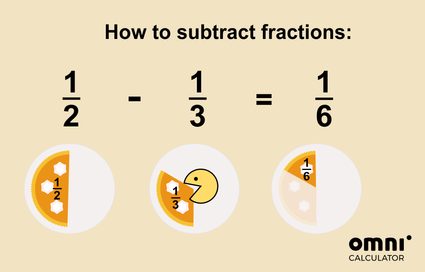
Isso não foi tão difícil, foi?

A multiplicação de frações é, felizmente, uma operação fácil. É: numerador vezes numerador sobre denominador vezes denominador. Às vezes, você também precisa simplificar a fração. E é isso!

Dê uma olhada neste exemplo:

➽ ²/₃ × ⁵/₆ = ^{(2 × 5)}/_{(3 × 6)} = ¹⁰/₁₈

que você pode simplificar para ⁵/₉

Quando você lidar com frações mistas, não se esqueça de que você deve sempre escrevê-las como uma fração imprópria antes de multiplicar:

➽ 2 ¹/₂ × 3 ¹/₄ = ⁵/₂ × ¹³/₄ = ^{(5 × 13)}/_{(2 × 4)} = ⁶⁵/₈ = 8 ¹/₈

Ao multiplicar uma fração por um número inteiro, lembre-se de que você pode escrever o número inteiro como ele mesmo dividido por 1:

➽ 3 × ⁵/₇ = ³/₁ × ⁵/₇ = ^{(3 × 5)}/_{(1 × 7)} = ¹⁵/₇

Se você não sabe como lidar com a redução de frações, role para baixo até a seção "Como simplificar frações".

Agora que você sabe como multiplicar frações, vamos passar para o próximo tópico, divisão de frações.

Você está se perguntando como dividir frações? Não se preocupe! A divisão de frações é bastante semelhante à multiplicação de frações. A única diferença é que você deve multiplicar o primeiro número pela recíproca da segunda fração. Pode parecer um pouco estranho, mas é muito simples! Dê uma olhada neste exemplo:

(¹/₂) / (³/₅) = ¹/₂ × ⁵/₃ = ^{(1 × 5)}/_{(2 × 3)} = ⁵/₆

Portanto, tudo o que você precisa fazer é virar a segunda fração de cabeça para baixo (que é sua recíproca) e multiplicar as frações. Às vezes, você também pode precisar fazer alguma redução de fração. E isso é tudo! 🎉

Sempre gostamos de simplificar nossas vidas, até mesmo na matemática. É por isso que simplificar frações é algo tão importante. Isso significa que escrevemos a fração em sua forma mais simples possível. Também chamamos a simplificação de frações de redução de frações.

Mas o que isso significa exatamente? Dê uma olhada nestes exemplos:

• Você prefere dizer que sobrou um quarto (um quarto) da pizza, em vez de dois oitavos, certo?
• ou que você comeu metade de um bolo, e não três sextos

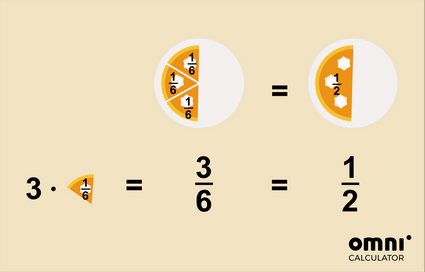
Para simplificar uma fração, você pode usar dois métodos:

1. Use uma abordagem mais simples: dividindo o numerador e o denominador por 2, 3, 5, 7, 11... até que seja impossível continuar a divisão (sem um resto):

   ➽ ⁴²/₁₂₆ = ^{(42➗ 2)}/_{(126 ➗ 2)}

   ➽ ²¹/₆₃ = ^{(21 ➗ 3)}/_{(63 ➗ 3)}

   ➽ ⁷/₂₁ = ^{(7 ➗ 7)}/_{(21 ➗ 7)}

   ➽ ¹/₃

2. Encontre o MDC (máximo divisor comum), do numerador e do denominador e, em seguida, divida-os por esse número: MDC(42,126) = 42, portanto

   ➽ ⁴²/₁₂₆ = ^{(42 ➗ 42)}/_{(126 ➗ 42)}

   ➽ ¹/₃

Leia mais sobre como reduzir frações em nossa calculadora para simplificar frações 🇺🇸. Além disso, não deixe de dar uma olhada em nossa incrível calculadora de frações equivalentes 🇺🇸, que pode te ajudar a encontrar muitas representações equivalentes para sua fração.

Se quiser descobrir como converter um decimal em uma fração, você está no lugar certo. É claro que você também pode usar nossa calculadora de decimal para fração e deixar que ela faça todo o trabalho. Abaixo você encontra um guia passo a passo para realizar a conversão:

Vamos supor que você queira converter 0,32 em uma fração:

1. Trate seu decimal como um numerador. Então, o denominador será 1.

2. Mova a vírgula para a direita, até que você tenha apenas um número inteiro:

   0,32 → 3,2 → 32

   Cada movimento corresponde à multiplicação por 10

   0,32 ⋅ 10 → 3,2 ⋅ 10 → 32

3. Você multiplicou o numerador por 10 ⋅ 10, e agora precisamos multiplicar o denominador pelo mesmo número:

   1 ⋅ 10 ⋅ 10 = 100

4. Você transformou sua fração em um decimal! ✨ 0,32 → ³²/₁₀₀

5. Por fim, simplifique o resultado. Como o máximo divisor comum para 32 e 100 é 4, divida o numerador e o denominador por esse valor:

   ➽ ³²/₁₀₀ = ⁸/₂₅

E é isso, a fração em sua forma mais simples. ❤️

Bem, a maneira mais fácil de transformar uma fração em um decimal é... usar uma calculadora. Seja esta calculadora de frações, uma calculadora de bolso padrão ou nossa ferramenta dedicada, o conversor de fração para decimal 🇺🇸.

Às vezes, é relativamente fácil transformar a fração em decimal sem nenhuma ferramenta, como 1/2, 3/4 (ou até 1/8). Acreditamos que você possa descobrir como expandir as frações acima para terem os fatores 10, 100, 1000, etc em seus denominadores, respectivamente:

• Multiplique ¹/₂ por 5 para obter 10 como denominador:

  ➽ ¹/₂ = ⁵/₁₀ = 0,5

• Multiplique ³/₄ por 25 para obter 100 como denominador:

  ➽ ³/₄ = ⁷⁵/₁₀₀ = 0,75

• Multiplique ¹/₈ por 125 para obter 1000 como denominador:

  ➽ ¹/₈ = ¹²⁵/₁₀₀₀ = 0,125

Mas e se você não tiver a Internet ou uma calculadora com você, apenas papel e caneta📝? E se sua fração não parece tão fácil de expandir como as anteriores? Então, você provavelmente precisará fazer uma divisão à mão com as casas decimais. Boa sorte! 🤞

Você precisa encontrar um denominador comum antes de fazer isso. Usaremos 1/2 e 3/5 como exemplo. Siga estas etapas para somar frações com denominadores diferentes:

1. Você precisa encontrar o mínimo múltiplo comum (MMC) do denominador.

   10

2. Divida o MMC por cada denominador e multiplique os numeradores pela resposta:

   • 10/2 = 5
     5 ⋅ 1 = 5

   • 10/5 = 2
     2 ⋅ 3 = 6

3. Você pode somar os números encontrados na Etapa 2 e colocar a resposta sobre o MMC:

   • 6 + 5 = 11

   • 11/10 = 1 ¹/₁₀

4. Pronto! Você somou suas frações.

Sim, toda fração é um número racional, mas nem todos os números racionais são frações. Um número racional é uma fração somente quando o numerador e o denominador são números inteiros.

0,3333 escrito como uma fração é ³³³³/₁₀₀₀₀.

Para você encontrar essa resposta:

1. Escreva o decimal como o numerador e 1 como o denominador:

   0,3333/1

2. Mova a vírgula para a direita no final do número para que este apareça como um inteiro:

   3333

3. Adicione o mesmo número de zeros ao denominador que o número de casas que você moveu a vírgula. Nesse caso, são quatro:

   10000

4. Coloque o número da Etapa 2 como o numerador e o número da Etapa 3 como o denominador:

   3333/10000

O produto de 1/2 e 5/3 é 5/6.

Para chegar a essa resposta, multiplicamos os numeradores e denominadores nas seguintes etapas:

• 1 ⋅ 5 = 5; e

• 2 ⋅ 3 é 6; portanto

• 1/2 ⋅ 5/3 = 5/6