Calculadora de Crescimento Exponencial
Há um número substancial de processos para os quais você pode usar essa calculadora de crescimento exponencial. A regra geral é que a fórmula de crescimento exponencial:
é usada quando há uma quantidade com um valor inicial, , que muda ao longo do tempo, , com uma taxa de variação, . A função exponencial que aparece na fórmula acima tem uma base igual a .
Observe que a taxa de variação representa um crescimento exponencial, , se for um número positivo, mas esta calculadora também funciona como uma calculadora de decaimento exponencial. Neste caso, terá valores negativos, caracterizando uma taxa de decaimento, a qual deve estar entre 0 e -100%. A razão para isso é que você não pode ter um decaimento de mais de 100% em relação à quantidade inicial, pois isso resultaria em um valor negativo.
A equação de crescimento exponencial é usada em diversas aplicações. Verifique a nossa calculadora de datação por radiocarbono (datação por carbono 14) 🇺🇸. Outra aplicação é a reação em cadeia da polimerase (você pode descobrir o porquê com a calculadora de temperatura de recozimento 🇺🇸 da Omni), bem como no cálculo de juros compostos. Se quiser saber mais sobre esse assunto, consulte a calculadora de juros compostos da Omni. Para obter mais exemplos de onde você pode usar essa fórmula, consulte abaixo.
Como calcular o crescimento exponencial
Considere o seguinte problema: a população de uma pequena cidade no início de 2019 era de 10.000 pessoas. Você percebeu que a população da cidade cresce a uma taxa constante de 5% ao ano. O que você deve fazer para calcular o tamanho projetado da população no ano de 2030? Com base nos dados fornecidos, podemos concluir que o valor inicial da população, , é igual a 10.000. Além disso, temos uma taxa de crescimento de .
Portanto, a fórmula de crescimento exponencial que devemos usar é:
Aqui é o número de anos passados desde 2019. Em nosso caso, para o ano de 2030, devemos usar , pois essa é a diferença no número de anos entre 2030 e o ano inicial de 2019. Finalmente, obtemos:
Portanto, o número projetado de habitantes de nossa pequena cidade no ano de 2030 será de cerca de 17.103.
Se quiser se aprofundar um pouco mais nessa fórmula específica, você pode usar nossa calculadora de crescimento exponencial para descobrir o número projetado de habitantes para cada ano, a partir de 2019. Esse cálculo resulta na tabela a seguir, na qual arredondamos os resultados para o número inteiro mais próximo:
ano | ||
|---|---|---|
2019 | 0 | 10.000 |
2020 | 1 | 10.500 |
2021 | 2 | 11.025 |
2022 | 3 | 11.576 |
2023 | 4 | 12.155 |
2024 | 5 | 12.763 |
2025 | 6 | 13.401 |
2026 | 7 | 14.071 |
2027 | 8 | 14.775 |
2028 | 9 | 15.513 |
2029 | 10 | 16.289 |
2030 | 11 | 17.103 |
Se quiser ter uma noção ainda melhor do crescimento da população, você pode representar esses dados graficamente, com o eixo horizontal sendo o eixo do tempo e o eixo vertical representando o valor da população . Os dados da tabela são todos os pontos situados no gráfico contínuo da função de crescimento exponencial:
Como a base dessa função exponencial é 1,05, e como ela é maior que 1, o gráfico de crescimento exponencial que obtemos é crescente. A principal diferença entre esse gráfico e o gráfico da função exponencial normal é que sua interceptação y não é 1, mas sim 10.000, o que corresponde ao valor inicial :
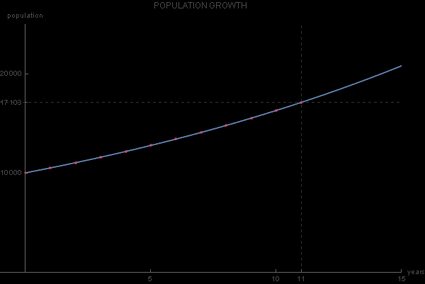
A partir desse exemplo, podemos ver as possíveis limitações do modelo de crescimento exponencial. É improvável que a taxa de crescimento permaneça constante ao longo do tempo. Ou seja, é difícil esperar que a taxa anual de crescimento da população da cidade permaneça em 5% por uma década ou mais.
Em situações da vida real, há oscilações naturais da taxa de crescimento que não estão incluídas nesse modelo de crescimento exponencial. Um modelo mais realista de crescimento populacional é o modelo de crescimento logístico, que conta com a capacidade de carga, uma constante que representa o limite de crescimento natural da população.
Como encontrar o momento em que a quantidade inicial atinge um determinado valor
Continuando com nosso exemplo da pequena cidade, a próxima pergunta que você pode se fazer é: "quando podemos esperar que a população alcance algum determinado valor?" Isso pode ser útil se você quiser saber quando ajustar o planejamento urbano da cidade para uma população maior. Suponha que a prefeitura se pergunte, quando a população da cidade terá triplicado de tamanho em relação aos 10.000 habitantes originais. Ou seja, quando a população atingirá 30.000 pessoas?
Aqui sabemos quanto é , mas não sabemos o valor de t quando isso ocorrerá. Vamos fazer isso passo a passo:
-
Insira na fórmula:
-
Depois de dividir os dois lados da equação por 10.000, obtemos: .
-
Tome o logaritmo para a base 1,05 de ambos os lados dessa equação: .
-
Use o logaritmo para finalmente obter: .
Portanto, a resposta à pergunta da prefeitura é aproximadamente 22 anos após 2019, ou seja, em 2041:"
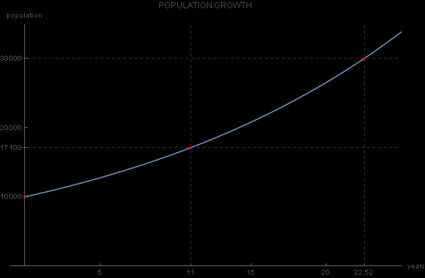
O tempo pode ser negativo?
Você já deve ter notado um problema com o crescimento e o decaimento exponencial: ele naturalmente trata o tempo apenas como um valor positivo, portanto, estamos prevendo uma quantidade futura. No entanto, isso não nos impede de usar essa fórmula com valores de tempo negativos. Isso significa que descrevemos o fenômeno de interesse no tempo antes da observação inicial ter sido feita.
No caso do crescimento populacional, você pode fazer a seguinte pergunta: qual era a população de nossa pequena cidade no ano 2000, supondo que a taxa de crescimento populacional fosse de 5%?
Para resolver isso, você usaria , já que o ano 2000 precede o ano 2019 em 19 anos. Portanto, a resposta seria
habitantes, como você também pode ver neste gráfico:
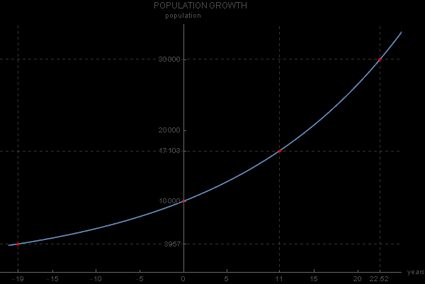
Outra forma de escrever a equação de crescimento exponencial
Para algumas aplicações, por exemplo, ao calcular o decaimento exponencial de uma substância radioativa, uma maneira alternativa de escrever a fórmula de crescimento e decaimento exponencial é:
O coeficiente desempenha o papel da taxa de crescimento, do mesmo modo que na fórmula original de crescimento exponencial. Comparando a equação acima com a original, você pode ver que a relação entre e é a seguinte:
o que significa
e .
Exemplo de como usar a fórmula de decaimento exponencial
O decaimento radioativo é um exemplo bem conhecido de como a fórmula de decaimento exponencial é usada. Para uma determinada quantidade inicial de substância radioativa, você pode escrever a lei que rege seu decaimento ao longo do tempo. Mas talvez um exemplo mais divertido seja medir qual a quantidade de café que permanece em seu corpo às 22h se você bebeu uma xícara de café com de cafeína ao meio-dia.
Usaremos que a meia-vida da cafeína no corpo humano é de aproximadamente seis horas. Esse é um termo definido como o tempo necessário para que uma determinada quantidade seja reduzida à metade de seu valor inicial. Saiba mais com a calculadora de meia-vida da Omni. Portanto, neste exemplo, temos:
Aqui, será mais fácil usar a notação alternativa para a fórmula de crescimento exponencial:
.
Aqui está o cálculo passo a passo:
-
Insira x(6)= 47,5 e t = 6 na equação: .
-
Após dividir os dois lados da equação por 95 e aplicar o logaritmo natural, essa expressão será: .
-
Usando o logaritmo natural, obtemos: .
-
Portanto, a fórmula de decaimento exponencial em nosso exemplo é: .
-
Como 22h é dez horas depois do meio-dia, queremos saber a quantidade de cafeína em . Temos: .
Portanto, às 22 horas, a quantidade de cafeína restante em seu corpo será de aproximadamente 30 mg.
E se você não tiver o tempo?
O tempo pode ser expresso basicamente em qualquer unidade apropriada. Para alguns problemas, serão segundos, para outros, anos. Você deve escolher a unidade de tempo de forma que corresponda à natureza do processo observado. Por exemplo, se quiser entender a mudança na população de uma cidade, você deve escolher anos. Por outro lado, se você for calcular a quantidade de café restante em seu corpo depois de ter bebido uma xícara, a unidade de tempo apropriada deve ser horas ou talvez minutos.
Observe que não precisa ser considerado apenas como tempo. Em alguns casos, a variável que mede a taxa de alteração pode ser diferente do tempo. Por exemplo, ao estudar a maneira como a pressão atmosférica muda com a altitude, a variável que mede esta mudança é a distância, e você deve escolher metros como as unidades de mudança apropriadas. Nossa calculadora da pressão atmosférica em altitude pode ajudar você neste caso.
Como diferentes taxas de crescimento exponencial afetam o crescimento
A diferença na taxa de crescimento exponencial r terá uma influência significativa na rapidez com que a quantidade observada muda, em relação ao valor inicial. Vamos começar com e, usando a calculadora de crescimento exponencial, ver qual será x(10) para quatro valores diferentes de :
1% | 100 | 110,5 |
3% | 100 | 134,4 |
5% | 100 | 162,9 |
10% | 100 | 259,4 |
Nesta tabela, vemos que todos os valores iniciais são os mesmos, sendo iguais a , mas os valores finais de diferem significativamente. Sua intuição pode te enganar aqui, porque a diferença entre 1% e 3% não parece muito grande, mas após dez períodos, isso equivale a um aumento de 21,67% para , considerando um crescimento de 3% quando comparado ao crescimento de 1%."
Se você comparar o crescimento de 10% com o crescimento de 5%, perceberá uma diferença ainda maior, 59,23% a favor do crescimento de 10%. Você pode observar esse contraste na seguinte representação gráfica das quatro funções de crescimento exponencial:
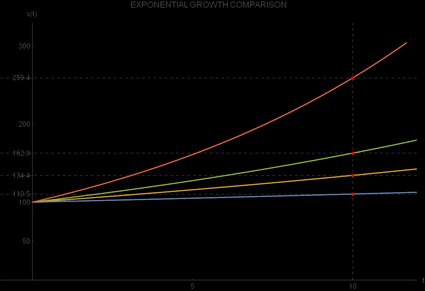
Quais são as aplicações do crescimento exponencial no mundo real?
A fórmula para crescimento e decaimento exponencial é usada para modelar vários fenômenos do mundo real:
- crescimento populacional de bactérias, vírus, plantas, animais e pessoas;
- decaimento de matéria radioativa;
- concentração de drogas no sangue;
- pressão atmosférica do ar em uma determinada altura;
- juros compostos e crescimento econômico;
- datação por radiocarbono;
- capacidade de processamento dos computadores etc.
💡 E você sabia que...
Você pode verificar se um conjunto de números obedece à fórmula de crescimento exponencial usando a conhecida Lei de Benford?
Referências
FAQs
Como faço para calcular o crescimento exponencial?
O crescimento exponencial é descrito pela fórmula:
Xt = X₀ × (1 + r/100)ᵗ
em que Xt é a quantidade no tempo t, X₀ é o valor inicial, r é a taxa de variação.
Qual é a diferença entre crescimento exponencial e linear?
O crescimento exponencial ocorre pela multiplicação do valor inicial por algum fator constante em cada etapa de tempo. Crescimento linear significa que você adiciona a mesma quantidade em cada etapa de tempo.
Como faço para calcular o decaimento exponencial?
O decaimento exponencial é dado pela fórmula:
Xt = X₀ × exp(μt)
em que Xt é a quantidade no tempo t, X₀ é a quantidade inicial e μ é a constante de decaimento.