Calculadora de Soma de Vetores

Boas-vindas à calculadora de soma de vetores da Omni, onde você aprenderá tudo sobre soma de vetores em 2D ou 3D. Nossa ferramenta permite que você forneça os dois vetores usando coordenadas cartesianas ou a magnitude e o ângulo. Como bônus, ela pode usar múltiplos dos vetores para somá-los ou funcionar como uma calculadora de subtração de vetores. E para os momentos em que você não tem a ferramenta da Omni à mão, fornecemos a fórmula de adição de vetores e descrevemos em detalhes como somar vetores usando a regra do paralelogramo.

Você prefere assistir ao invés de ler? Confira nossa videoaula sobre subtração e adição de vetores aqui:

Do ponto de vista matemático, um vetor é uma sucessão ordenada de números (um par em 2D, um trio em 3D e mais em dimensões superiores). É claro que os cientistas têm uma definição mais técnica para esses objetos. Em geral, um vetor é um elemento de um espaço vetorial. Essa explicação parece bastante simples até que você saiba que, para os matemáticos, os espaços vetoriais podem consistir em sequências, funções, permutações, matrizes, etc. Felizmente, não precisamos de nada disso nesta calculadora de soma de vetores.

Por outro lado, os físicos preferem pensar nos vetores como setas (que são sua representação visual) anexadas a objetos. Dessa forma, eles representam as forças agindo sobre um objeto, como, por exemplo, a gravidade, o arrasto ou a força magnética. O sentido das setas nos informa... bem, o sentido da força, enquanto o seu comprimento indica o módulo da força.

Felizmente, ambas as abordagens são essencialmente as mesmas, pelo menos no nosso caso e nesta calculadora de adição de vetores. Ainda assim, podemos representar os vetores de duas maneiras: usando coordenadas cartesianas ou a magnitude e o ângulo. No entanto, o último é possível somente no caso bidimensional, pois corresponde, a representação em termos de coordenadas polares.

Vejamos um exemplo. Um vetor v= (2,1) em 2D (já que tem duas coordenadas) nos diz, em essência, que tem duas unidades ao longo do eixo X e uma ao longo do eixo Y. Observe que as coordenadas positivas significam que você está contando as unidades para a direita e para cima (ao longo dos eixos horizontal e vertical, respectivamente), enquanto as negativas indicam o sentido oposto. Da mesma forma, se adicionarmos uma terceira coordenada, digamos, w= (2,1,5), teremos um sistema em 3D, onde o 5 extra corresponde ao movimento ao longo do sentido positivo do eixo Z.

Como alternativa, podemos representar o vetor bidimensional v usando sua magnitude m e direção θ. A primeira é simplesmente o comprimento do vetor. A última é o ângulo no sentido anti-horário, iniciando na metade positiva do eixo horizontal até o vetor, quando este último for desenhado no plano com seu ponto inicial em (0,0).

Em particular, isso significa que m não deve ser negativo, enquanto θ deve estar entre 0 e 360 graus (ou entre 0 e 2π em radianos), embora essa calculadora de soma vetorial aceite outros valores de ângulo de acordo com as mesmas regras que regem as funções trigonométricas e seus argumentos.

Mencionamos que existe um equivalente das coordenadas polares (magnitude e direção) em 3D chamado de coordenadas esféricas. No entanto, neste contexto de soma de vetores, elas tendem a ser confusas e são muito menos comuns em termos práticos, por isso as ignoramos em nossa calculadora de soma de vetores. Ainda assim, você pode saber mais sobre elas em nossa calculadora de coordenadas esféricas 🇺🇸.

Muito bem, já conhecemos bastante o objeto com o qual estamos lidando. Agora, veremos como somá-los.

A soma de vetores é fácil, especialmente quando temos coordenadas cartesianas. Para ser preciso, basta somar os números das coordenadas. Isso significa que a fórmula de soma de vetores em 2D é a seguinte:

(a,b) + (d,e) = (a + d, b + e),

e a fórmula em 3D é

(a,b,c) + (d,e,f) = (a + d, b + e, c + f).

E isso é tudo! É bom que você tenha uma fórmula simples para variar, não é mesmo?

Em 2D, se usarmos a representação de magnitude, direção e sentido, a notação fica um pouco mais complicada. Infelizmente, nesse caso, não podemos simplesmente somar os valores dos dois vetores como fizemos com as coordenadas cartesianas. Damos uma excelente explicação visual do porquê isso acontece usando a Regra do Paralelogramo na próxima seção.

No entanto, suponha que você não tenha vontade de desenhar os vetores. Nesse caso, a melhor maneira de encontrar a soma deles é simplesmente encontrar sua representação em coordenadas cartesianas e usar a fórmula de adição de vetores do início desta seção.

Certamente, ajuda sabermos que a transição de uma representação de soma para outra é relativamente simples. Assim, se um vetor v tiver magnitude m e formar um ângulo θ com o eixo horizontal, então, v= (x,y) em coordenadas cartesianas com:

x = m ⋅ cos(θ) e y = m ⋅ sen(θ),

onde cos e sen são as funções trigonométricas cosseno e seno, respectivamente (saiba mais sobre elas na calculadora de funções trigonométricas 🇺🇸 da Omni). Para completar, vamos mencionar também a fórmula de transição das coordenadas polares para as cartesianas:

m = √(x² + y²) e θ = arccos(x / m),

onde arccos é a função arco cosseno (entenda suas características em nossa calculadora de arco cosseno 🇺🇸).

Antes de mostrarmos a você a regra do paralelogramo, vamos mencionar algumas funcionalidades adicionais da calculadora de soma de vetores.

1. Calculadora de subtração de vetores
   Em vez de somar vetores, você pode querer encontrar a diferença (subtrair) entre eles. As regras são as mesmas de antes: subtraímos os vetores coordenada por coordenada. Para usar essa opção, basta escolher Subtração em Operação na ferramenta, e ela se tornará uma calculadora de subtração de vetores.

2. Somando vetores com múltiplos
   Pode acontecer de você querer somar um vetor não uma vez, mas várias vezes. Por exemplo, v+ 4 ⋅w significaria adicionar quatro cópias de w a v. Em vez de usar a calculadora de adição de vetores quatro vezes para encontrar o resultado, você pode alterar a opção sem múltiplos para com múltiplos e informar os valores de α e β. Obviamente, você pode combinar essa opção com o ponto 1. e ter uma calculadora de subtração vetorial com múltiplos.

Na primeira seção deste artigo, mencionamos que representamos os vetores como setas. Até agora, só lidamos com eles algebricamente, como na fórmula de adição de vetores. Agora é hora de voltar aos desenhos. Para ser mais preciso, desenhar paralelogramos.

Basicamente, podemos pensar na soma de vetores como andar ao longo de um deles e depois ao longo do outro. Isso significa que, se desenharmos um deles como uma seta, então o "andar" ao longo dele se traduz em se mover da extremidade inicial até a final. Se quisermos nos mover ao longo do segundo vetor, podemos simplesmente desenhá-lo começando na extremidade final do primeiro vetor, e o vetor resultante será uma seta que começa na extremidade inicial do primeiro vetor e vai até a ponta da seta do segundo vetor.

Acima, descrevemos a ideia por trás da adição visual de vetores, e é nela que a regra do paralelogramo se baseia. Usando a regra do paralelogramo, temos por definição que: o vetor resultante da soma de dois vetores é a diagonal de um paralelogramo cujos lados são os dois vetores somados e desenhados a partir do mesmo ponto.

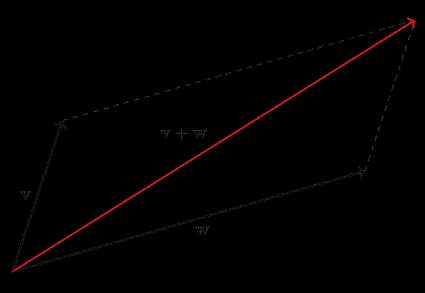
Na figura, podemos desenhar um paralelogramo a partir do vértice onde v e w começam, e desenhando uma reta paralela a v e uma paralela a w, representadas pelas linhas tracejadas. O vetor resultante será a diagonal deste paralelogramo. Este método é equivalente ao procedimento de soma abordado no início desta seção.

Com isso, concluímos a parte teórica desta calculadora. Agora, vamos colocar esse conhecimento em prática e ver como a calculadora de soma de vetores funciona.

Suponha que você queira encontrar a soma de um vetor v= (-3,2,8) e três múltiplos de w= (2,2,-4). Antes de fazermos isso à mão, vamos ver como podemos usar a calculadora de soma de vetores para encontrar a resposta.

Em primeiro lugar, observe que estamos adicionando vetores com três coordenadas (cartesianas), portanto eles são tridimensionais. Logo, precisamos escolher a opção "3D" em "Vetores em" e "Adição" no campo "Operação". Isso nos mostrará duas seções para as coordenadas, cada uma com três entradas marcadas como x, y e z, que correspondem à primeira, segunda e terceira coordenadas, respectivamente. Portanto, para representarmos v = (-3,2,8), utilizamos:

x = -3, y = 2, z = 8,

e no campo do vetor w= (2,2,-4), escrevemos:

x = 2, y = 2, z = -4.

Quando digitamos o último valor, podemos ver v + w no campo "Resultado". No entanto, este procedimento não resolve o nosso problema inicial. Gostaríamos de adicionar três múltiplos de w e não apenas um.

Portanto, escolhemos a opção "com múltiplos" na parte superior da calculadora, que calculará α ⋅v+ β ⋅w em vez de apenas v + w. Observe que usamos como padrão α = 1 e β = 1. Para o nosso problema, faremos a seguinte alteração:

α = 1, β = 3,

resultando no vetor desejado. No entanto, antes de revelar nosso resultado, vamos usar a fórmula de adição de vetores e encontrar a soma à mão.

Observe que adicionar três cópias de um vetor se traduz em adicionar três vezes suas coordenadas. Portanto,

v+ 3 ⋅w= (-3,2,8) + 3 ⋅ (2,2,-4) = (-3 + 3 ⋅ 2, 2 + 3 ⋅ 2, 8 + 3 ⋅ (-4)) = (3,8,-4).

É isso ai! Este exemplo não foi tão difícil assim, mas você pode imaginar como é repetir esses procedimentos com entradas terrivelmente complicadas. Ainda bem que temos a calculadora de soma de vetores da Omni para nos ajudar com esses problemas.

A soma dos vetores x = (x₁, x₂, ..., x_k) e y = (y₁, y₂, ..., y_k) é igual a:

x + y = (x₁ + y₁, x₂ + y₂, ..., x_k + y_k)

Ou seja, fazemos a adição coordenada por coordenada. Em particular, para vetores bidimensionais, obtemos:

(x₁, x₂) + (y₁, y₂) = (x₁ + y₁, x₂ + y₂)

Para realizar a soma destes vetores:

1. Some as coordenadas na primeira entrada: 2 + 1 = 3.
2. Some as coordenadas na segunda entrada: 1 + 0 = 1.
3. Escreva os resultados dos passos 1 e 2: (3,1).
4. É isso! Você acabou de realizar uma soma de vetores!

A fórmula para o módulo de x + y = (x₁ + y₁, x₂ + y₂) é a seguinte:

|x + y| = √[(x₁ + y)²+(x₂ + y₂)²]

Como você certamente notou, encontramos o módulo da soma de vetores usando o Teorema de Pitágoras!

A fórmula para o ângulo de direção da soma dos vetores x + y = (x₁ + y₁, x₂ + y₂) é a seguinte

θ = arctan((x₂ + y₂)/(x₁ + y₁))

em que arctan denota a função arco tangente (inversa da função tangente).