Calculadora de Perímetro

Q: O que é perímetro?

O perímetro é o comprimento de uma figura geométrica fechada . Ele também pode ser definido como a borda externa de uma área, simplesmente a linha contínua mais longa que circunda uma forma. O próprio nome vem do grego perimetros : peri que significa "ao redor" + metron , entendido como "medida". Como é o comprimento do contorno da forma, ele é expresso em unidades de distância, por exemplo, metros, pés, polegadas ou milhas. Read more

Q: É possível determinar a área com base no perímetro?

Em geral, não , não é possível calcular a área a partir do perímetro. Isso é particularmente verdadeiro para retângulos, paralelogramos, pipas e trapézios. Entretanto , para algumas formas específicas, como quadrados, hexágonos, polígonos regulares em geral e círculos, você pode determinar o lado (raio, no caso dos círculos) a partir do perímetro e, em seguida, calcular a área. Read more

Q: Qual é o perímetro de um edifício retangular de 20 m por 15 m?

O perímetro é de 70 m . Para chegar a esse resultado, você precisa somar o comprimento de todos os quatro lados do edifício. Dois lados de 20 m de comprimento somados dão 40 m, enquanto os outros dois lados de 15 m de comprimento somados dão 30 m. Juntos, obtemos 40 m + 30 m = 70 m, como afirmado. Read more

Com a calculadora de perímetro da Omni, você não precisa mais se preocupar com cálculos de perímetro. Abaixo, você encontrará as fórmulas de perímetro para doze formas geométricas diferentes, bem como um lembrete rápido sobre o que é perímetro e a definição de perímetro. Vá em frente, continue lendo esse artigo, ou confira uma ferramenta similar, nossa abrangente calculadora de área.

O que é perímetro?

O perímetro é o comprimento de uma figura geométrica fechada. Ele também pode ser definido como a borda externa de uma área, simplesmente a linha contínua mais longa que circunda uma forma. O próprio nome vem do grego perimetros: peri que significa "ao redor" + metron, entendido como "medida". Como é o comprimento do contorno da forma, ele é expresso em unidades de distância, por exemplo, metros, pés, polegadas ou milhas.

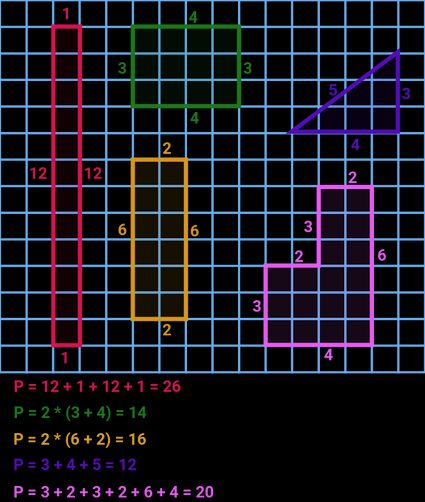
Como encontrar o perímetro: fórmulas de perímetro

Normalmente, a abordagem mais simples e direta é encontrar a soma de todos os lados de uma forma. Entretanto, há casos em que não há lados (como uma elipse, um círculo etc.) ou, um ou mais lados são desconhecidos. Neste parágrafo, listaremos todas as equações usadas nessa calculadora de perímetro.

Role para baixo até as próximas seções se você tiver curiosidade sobre uma forma específica e quiser ver uma explicação, derivação e imagem para cada uma das doze formas presentes nessa calculadora. Também temos ferramentas dedicadas a cada figura geométrica. Basta você digitar o nome da forma na barra de pesquisa na parte superior deste site.

Aqui estão as fórmulas de perímetro para as doze formas geométricas nesta calculadora:

Fórmula de perímetro do quadrado: $P = 4a$
Fórmula de perímetro do retângulo: $P = 2(a + b)$
Fórmulas de perímetro de triângulo:
- $P = a + b + c$ ; ou
- $P = a + b + \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma))}$ ; ou
- $P = a + \frac{a}{\mathrm{sen}(\beta + \gamma)} \times (\mathrm{sen}(\beta) + \mathrm{sen}(\gamma))$ .
Fórmula do perímetro do círculo: $P = 2\pi \cdot r$
Fórmula do perímetro do setor do círculo: $P = r(\alpha + 2)$ ( $\alpha$ está em radianos);
Fórmula do perímetro da elipse: $P = \pi\bigl[3(a + b) - \sqrt{(3a + b) \times (a + 3b)}\bigl]$ ;
Fórmula do perímetro do quadrilátero/trapézio: $P = a + b + c + d$
Fórmulas de perímetro de um paralelogramo:
- $P = 2(a + b)$ ;
- $P = 2a + \sqrt{2e^2 + 2f^2 - 4a^2}$ ; ou
- $P = 2(b + h/\mathrm{sen}(\alpha))$ .
Fórmulas de perímetro de um losango:
- $P = 4a$ ; ou
- $P = 2\sqrt{e^2 + f^2}$
Fórmula de perímetro de uma pipa: $P = 2(a + b)$
Fórmula de perímetro de uma coroa circular: $P = 2 \pi(R + r)$ .
Fórmula de perímetro do polígono regular: $P = n \cdot a$

Fórmula do perímetro de um quadrado

Um quadrado tem quatro lados de igual comprimento. Para calcular seu perímetro, tudo o que você precisa fazer é multiplicar o comprimento do lado por $4$ :

\begin{split} P_\mathrm{{quadrado}} &= a+a+a+a\\ &=4a \end{split}

Acredite ou não, mas a Omni também dispõe da calculadora do perímetro de um quadrado 🇺🇸!

Fórmula para o perímetro de um retângulo

A fórmula para o perímetro de um retângulo é quase tão fácil quanto a equação para o perímetro de um quadrado. A única diferença é que temos dois pares de lados de comprimento igual:

\begin{split} P_\mathrm{{retângulo}}& = a+b+a+b\\ &=2a+2b=2(a+b) \end{split}

Fórmula do perímetro de um triângulo

A fórmula mais fácil para calcular o perímetro de um triângulo é, como sempre, somar todos os lados:

P_{\mathrm{triângulo}} = a+b+c

triângulo, dados dois lados e o ângulo entre eles

No entanto, nem sempre você recebe três lados. O que você pode fazer? Bem, em vez de se preocupar, você pode usar a nossa calculadora da lei dos cossenos para encontrar o lado que falta:

c=\sqrt{a^2+b^2-2ab\times\cos(\gamma)}

Isso pode ser incorporado à fórmula do perímetro:

\begin{split} &P_{\mathrm{triângulo}} = a+b\\ &+\sqrt{a^2+b^2-2ab\times\cos(\gamma)} \end{split}

triângulo, dados dois ângulos e um lado entre eles

A outra opção é usar a lei dos senos se você tiver um lado e os dois ângulos adjacentes a esse lado:

b = \mathrm{sen\,}(\beta)\times\frac{a}{\mathrm{sen\,}(\beta+\gamma)}

e:

c = \mathrm{sen\,}(\gamma)\times\frac{a}{\mathrm{sen\,}(\beta+\gamma)}

portanto, o perímetro do triângulo pode ser expresso como:

\begin{split} P_{\mathrm{triângulo}} &= a+\frac{a}{\mathrm{sen\,}(\beta+\gamma)}\\ &\times(\mathrm{sen\,}(\beta)+\mathrm{sen\,}(\gamma)) \end{split}

Fórmula do perímetro de um círculo

O perímetro de um círculo também pode ser conhecido como circunferência. Para aprender mais, acesse a calculadora de circunferência. A fórmula mais conhecida do perímetro de uma circunferência usa apenas uma variável: o raio da circunferência:

\mathrm{C} = 2\pi\cdot r

Você já se perguntou quantas vezes a roda da sua bicicleta vai girar em uma viagem de 16 km? Bem, esse é um dos casos em que você precisará usar a fórmula da circunferência. Insira o raio de sua roda (metade do diâmetro da roda) e divida 16 km pela circunferência obtida (mas não se esqueça da conversão das unidades de comprimento!) Se quiser ser ainda mais preciso, você pode incluir o tamanho do pneu da bicicleta.

Fórmula do perímetro para um setor circular

Calcular o perímetro de um setor circular pode parecer complicado, é apenas o comprimento do arco ou é o comprimento do arco mais dois raios? Basta você ter em mente a definição de perímetro! O perímetro do setor é a soma dos comprimentos de todos os seus limites, portanto, é a última opção:

P_{\mathrm{setor\ circulo}} = r\cdot (\alpha+2)

em que $\alpha$ está em radianos.

Fórmula do perímetro de uma elipse

Embora a fórmula da área de uma elipse seja realmente simples e fácil de lembrar, a fórmula do perímetro de uma elipse é a mais problemática de todas as equações listadas aqui. Optamos por implementar uma das aproximações de Ramanujan nessa calculadora de perímetro:

\begin{split} &P_\mathrm{elipse} = \pi\cdot \bigl(3(a+b)\\ &-\sqrt{(3a+b)\cdot(a+3b)}\bigr) \end{split}

onde $a$ é o menor raio possível e $b$ é o maior raio possível de uma elipse. A outra aproximação de Ramanujan, mais precisa, é:

\begin{split} P_\mathrm{elipse} =\ &\pi\cdot(a+b)\\ &\cdot\frac{1+3\frac{(a-b)^2}{(a+b)^2}}{10+\sqrt{4-3\frac{(a-b)^2}{(a+b)^2}}} \end{split}

Há também uma forma mais simples, usando uma variável adicional $h$ :

h = \frac{(a-b)^2}{(a+b)^2}

ou seja:

\begin{split} P_\mathrm{elipse} =\ &\pi\cdot(a+b)\\ &\cdot\frac{1+3h}{10+\sqrt{4-3h}} \end{split}

Ou você pode simplesmente usar nossa calculadora!

Fórmula do perímetro de um trapézio

Se você quiser calcular o perímetro de um trapézio irregular, não há nenhuma fórmula especial, basta somar os quatro lados:

P_{\mathrm{trapézio}} = a+b+c+d

Talvez você tenha notado, mas essa é a fórmula para qualquer perímetro de quadrilátero.

Há também uma opção para determinados trapézios especiais, como um trapézio isósceles, cujos lados necessários são $a$ , $b$ e $c$ . Outro exemplo é um trapézio reto, em que o comprimento das bases e de um lado é suficiente para encontrar o perímetro da forma (para encontrar o último lado, usamos o Teorema de Pitágoras).

Fórmula do perímetro de um paralelogramo

Nesta calculadora de perímetro, você encontrará três fórmulas para calcular o perímetro de um paralelogramo:

A mais simples, somando todos os lados:

\quad\ \ P_{\mathrm{paralelogramo}} = 2(a+b)

paralelogramo, dado um lado e as diagonais

A fórmula do perímetro de um paralelogramo que requer um lado e as diagonais

\quad\ \ \begin{split} &P_{\mathrm{paralelogramo}} = 2a\\ &\qquad \ \ \ +\sqrt{2e^2+2f^2-4a^2} \end{split}

paralelogramo, dada a base, a altura e qualquer ângulo do paralelogramo

A equação do perímetro em termos da base, altura e qualquer ângulo do paralelogramo.

\ \ \ P_{\mathrm{paralelogramo}} = 2\left(b+\frac{h}{\mathrm{sen}(\alpha)}\right)

Fórmula do perímetro de um losango

A fórmula do perímetro de um losango não é uma ciência de foguetes, portanto, vamos torná-la concisa. Ela é a mesma fórmula do perímetro de um quadrado!

P_{\mathrm{losango}} = 4a

Outra solução para encontrar o perímetro do losango requer os comprimentos das diagonais:

P_{\mathrm{losango}} = 2\cdot\sqrt{e^2+f^2}

Tente derivar a fórmula você mesmo. Você sabe que as duas diagonais de um losango são perpendiculares e se interceptam, de modo que você pode dividir a forma em quatro triângulos retângulos congruentes. Cada triângulo tem lados com comprimento e/2 e f/2. Assim, tudo o que você precisa fazer é encontrar a hipotenusa do triângulo, que é, ao mesmo tempo, o lado do losango. Em seguida, você deve multiplicar o resultado por quatro para encontrar a fórmula final do perímetro do losango.

Fórmula do perímetro de uma pipa

A fórmula para o perímetro de uma pipa é bastante simples, basta somar todos os lados:

\begin{split} P_{\mathrm{kite}} &= a+a+b+b\\ &=2(a+b) \end{split}

Fórmula do perímetro de um anel

anel, dados os raios dos círculos externo e interno

Como o perímetro é definido como o contorno de uma forma geométrica, um anel exige que adicionemos a circunferência de ambos os círculos concêntricos:

\begin{split} P_{\mathrm{annulus}} &= 2\pi \cdot R+2\pi\cdot r\\ &=2\pi\cdot (R+r) \end{split}

Fórmula do perímetro de um polígono (pentágono regular, hexágono, octógono, etc.)

polígono regular, dado o comprimento do lado e o número de lados

Em nossa calculadora de perímetro, também implementamos uma fórmula simples para o perímetro de um polígono regular:

P_{\mathrm{polígono}}=n\cdot a

em que $n$ é o número de lados do polígono. Assim, por exemplo, você pode calcular o perímetro de um pentágono, hexágono ou octógono.

Além disso, para polígonos de até 12 lados, o nome do polígono aparecerá na ferramenta. Incrível, não é?

Se você quiser determinar o perímetro de qualquer polígono, some os comprimentos de todos os seus lados:

P_{\mathrm{polígono}}=\sum a_i

em que $a_1$ , $a_2$ , ..., $a_n$ são os comprimentos dos lados e $\sum$ é o símbolo da somatória (de $i = 1$ a $n$ ).

Ou use as coordenadas dos vértices:

\begin{split} P_{\mathrm{polígono}} = &\sum_{i=1}^n\Bigl((x_{i-1}-x_i)^2\\ &\qquad +(y_{i-1}-y_i)^2\Bigr) \end{split}

com $x_{n+1}=x_1$ e $y_{n+1}=y_1$ .

FAQ

Como calcular o perímetro de formas irregulares?

Para encontrar o perímetro de uma figura irregular:

Meça os comprimentos de todos os lados (externos).
Se os lados incluírem fragmentos circulares, meça o raio e o ângulo central, ou seja, o ângulo entre os raios que unem os dois pontos finais do arco ao centro.
Aplique a fórmula do perímetro do círculo para esse raio e tome a parte proporcional ao ângulo.
Some o comprimento de todos os lados.

É possível determinar a área com base no perímetro?

Em geral, não, não é possível calcular a área a partir do perímetro. Isso é particularmente verdadeiro para retângulos, paralelogramos, pipas e trapézios. Entretanto, para algumas formas específicas, como quadrados, hexágonos, polígonos regulares em geral e círculos, você pode determinar o lado (raio, no caso dos círculos) a partir do perímetro e, em seguida, calcular a área.

Qual é o perímetro de um edifício retangular de 20 m por 15 m?

O perímetro é de 70 m. Para chegar a esse resultado, você precisa somar o comprimento de todos os quatro lados do edifício. Dois lados de 20 m de comprimento somados dão 40 m, enquanto os outros dois lados de 15 m de comprimento somados dão 30 m. Juntos, obtemos 40 m + 30 m = 70 m, como afirmado.