Calculadora de Círculo Unitário

Boas-vindas à calculadora do círculo unitário da Omni ⭕. Nossa ferramenta ajudará você a determinar as coordenadas de qualquer ponto de um círculo unitário. Basta inserir o ângulo ∡ e mostraremos a você o seno e o cosseno desse ângulo.

Se você não tiver certeza do que é um círculo unitário, role para baixo e você encontrará a resposta. O gráfico de círculo unitário e uma explicação sobre como encontrar a tangente do círculo unitário, o seno e o cosseno também estão aqui, portanto, não espere mais! Se quiser aprender outras propriedades das funções trigonométricas, não deixe de acessar a nossa calculadora de trigonometria!

Um círculo unitário, também conhecido como círculo trigonométrico, é um círculo com um raio igual a 1 (raio unitário). Na maioria dos casos, ele é centralizado no ponto $(0,0)$, a origem do sistema de coordenadas.

O círculo unitário é um conceito muito útil quando você quer aprender trigonometria e conversão de ângulos.

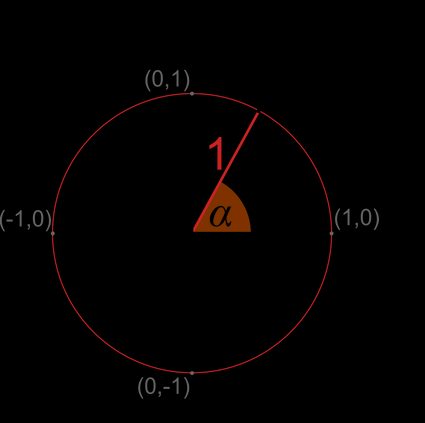
Agora que você sabe o que é um círculo unitário, vamos prosseguir com as relações trigonométricas no contexto do círculo unitário.

OK, então por que o círculo unitário é tão útil na trigonometria?

Explicação curta:

Relações do círculo unitário para seno e cosseno:

• Seno é a coordenada y; e
• Cosseno é a coordenada x

Explicação padrão:

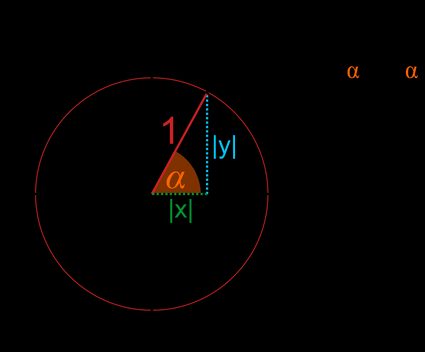
Tomemos qualquer ponto A na circunferência do círculo unitário.

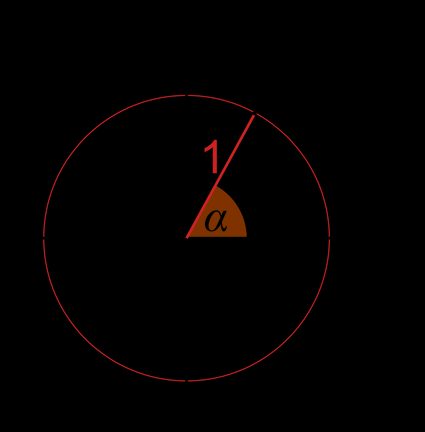
• As coordenadas desse ponto são $x$ e $y$. Como se trata de um círculo unitário, o raio r é igual a $1$ (a distância entre o ponto $P$ e o centro do círculo).

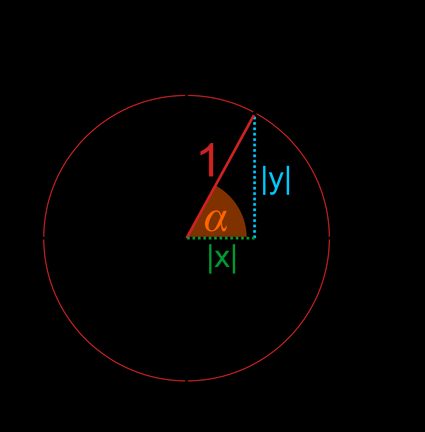
• Ao projetar o raio nos eixos x e y, você obterá um triângulo retângulo, onde $|x|$ e $|y|$ são os comprimentos dos catetos e a hipotenusa é igual a $1$.

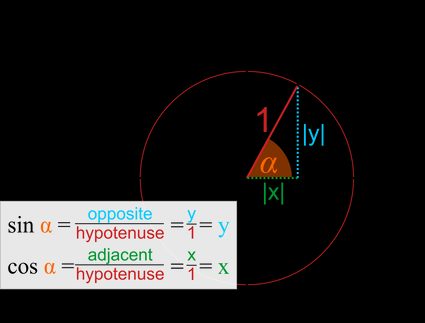
• Como em todo triângulo retângulo, você pode determinar os valores das funções trigonométricas encontrando as proporções dos lados:

Portanto, em outras palavras, o seno é a coordenada y:

E o cosseno é a coordenada x.

A equação do círculo unitário, que vem diretamente do teorema de Pitágoras, é a seguinte:

Ou, analogamente:

Essa conexão entre trigonometria e triângulos é mesmo surpreendente! Saiba mais sobre esses conceitos importantes na nossa calculadora de triângulo retângulo.

Você pode encontrar o valor da tangente a partir do círculo unitário diretamente se lembrar da definição de tangente:

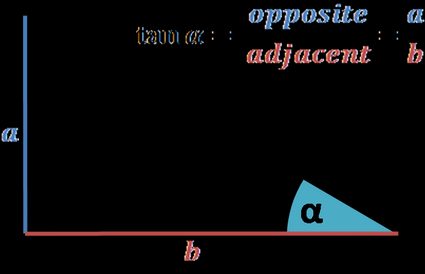
A razão entre os catetos opostos e adjacentes de um ângulo em um triângulo retângulo

Como aprendemos na seção anterior ("Círculo unitário: seno e cosseno"), $\text{sen}(\alpha) = y$ e $\cos(\alpha) = x$, então:

Também podemos definir a tangente do ângulo como seu seno dividido pelo cosseno:

O que, é claro, nos dará o mesmo resultado.

Outro método muito melhor é usar nossa calculadora de círculo unitário. 😁

Mas e se você não estiver satisfeito apenas com essa fórmula e quiser realmente ver a tangente no seu círculo unitário?

Isso é um pouco mais complicado do que determinar o seno e o cosseno, que são simplesmente as coordenadas. Há duas maneiras de mostrar a tangente no círculo unitário:

Método 1:

1. Crie uma reta tangente ao círculo, passando ponto $A$.
2. Ela cruzará o eixo x no ponto $B$.
3. O comprimento do segmento $\bar{AB}$ é o valor da tangente

Método 2:

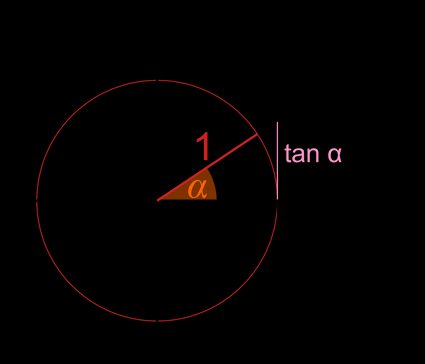
1. Desenhe uma reta vertical em $x = 1$.
2. Aumente a reta que contém o raio até que ela toque a reta vertical.
3. Nomeie a interseção dessas duas retas como ponto $C$.
4. A tangente, $\tan(\alpha)$, é a coordenada y do ponto $C$.

Em ambos os métodos, criamos triângulos retângulos com seus catetos adjacentes iguais a 1 😎

O seno, o cosseno e a tangente não são as únicas funções que você pode construir no círculo unitário. Além da função cotangente, você também pode apresentar outras funções menos conhecidas, por exemplo, secante, cossecante e o seno verso:

O conceito de círculo unitário é muito importante porque você pode usá-lo para encontrar o seno e o cosseno de qualquer ângulo. Apresentamos abaixo alguns ângulos comumente encontrados no gráfico do círculo unitário:

Por exemplo, como você pode determinar $\mathrm{sen}(150\degree)$?

1. Procure o ângulo $150\degree$.
2. Como aprendemos antes, o seno é a coordenada y, portanto, tomamos a segunda coordenada do ponto correspondente no círculo unitário:

Como alternativa, insira o ângulo de 150° em nossa calculadora de círculo unitário. Mostraremos a você o valor $\mathrm{sen}(150\degree)$ da coordenada y, bem como o cosseno, a tangente e o gráfico do círculo unitário.

Bem, depende do que você quer memorizar 🙃. Há duas coisas a serem lembradas quando se trata do círculo unitário:

1. Conversão de ângulos, ou seja, como você pode mudar entre um ângulo em graus e um em termos de $\pi$ (radianos do círculo unitário); e

2. As funções trigonométricas dos ângulos populares.

Vamos começar com a primeira parte mais fácil. Os ângulos mais importantes são aqueles que você usará o tempo todo:

• $30\degree = \pi/6$;
• $45\degree = \pi/4$;
• $60\degree = \pi/3$;
• $90\degree = \pi/2$; e
• Ângulo total, $360\degree = 2\pi$.

Como esses ângulos são muito comuns, tente memorizá-los ❤️. Para qualquer outro ângulo, você pode usar a fórmula para conversão de ângulos:

A conversão dos radianos do círculo unitário em graus não deve mais ser um problema! 💪

A outra parte: lembrar de todo o gráfico do círculo unitário, com valores de seno e cosseno. Este é um processo um pouco mais longo. Não vamos descrevê-lo aqui, mas fique à vontade para conferir essas dicas de como memorizar ângulos a partir do círculo unitário ou esta página sobre como memorizar o círculo unitário rapidamente. Se você preferir assistir a vídeos 🖥️ a ler 📘, assista a um desses dois vídeos que explicam como memorizar o círculo unitário:

• Como memorizar os ângulos de um círculo unitário; e
• Como montar o círculo unitário

Além disso, esta tabela com ângulos comumente usados pode ser útil:

E se algum método falhar, sinta-se à vontade para usar nossa calculadora de círculo unitário, ela sempre estará aqui para te ajudar ❤️. Esperamos que esta ferramenta permita que você entenda e memorize os parâmetros que podem ser obtidos a partir do círculo unitário!

tan 30° = 1/√3. Para obter essa resposta no círculo unitário, começamos encontrando os valores de sen e cos a partir das coordenadas y e x, respectivamente: sen 30° = 1/2 e cos 30° = √3/2. Agora, use a fórmula. Lembre-se de que tan 30° = sen 30° / cos 30° = (1/2) / (√3/2) = 1/√3, como afirmado. Está vendo como é fácil?

Para determinar a cossecante de θ no círculo unitário:

1. A partir do centro do círculo, desenhe o raio correspondente ao ângulo θ.
2. Desenhe retas tangentes à circunferência nos pontos (0,1) e (0,-1).
3. Estenda o raio da Etapa 1 de modo que ele intercepte uma dessas tangentes.
4. A distância do centro até o ponto de interseção da Etapa 3 é a cossecante do seu ângulo θ.
5. Se não houver um ponto de interseção, a cossecante de θ é indefinida (isso acontece quando sen θ = 0).

Como o arco-seno é a função inversa do seno, encontrar arcsen(1/2) é equivalente a encontrar um ângulo cujo seno seja igual a 1/2. No círculo unitário, os valores do seno são as coordenadas y dos pontos na circunferência. Ao inspecionar o círculo unitário, vemos que a coordenada y é igual a 1/2 para o ângulo π/6, ou seja, 30°.