Calculadora do Ângulo entre Dois Vetores

Com esta calculadora do ângulo entre dois vetores da Omni, você aprenderá rapidamente como encontrar o ângulo entre dois vetores. Não importa se seus vetores estão em 2D ou 3D, nem se suas representações são coordenadas ou pontos extremos, isto é, pontos iniciais e finais, nossa ferramenta é uma aposta segura em todos os casos. Brinque com a calculadora e verifique as definições e explicações abaixo. Se você estiver procurando as fórmulas do ângulo entre dois vetores, com certeza encontrará-las aqui.

Neste parágrafo, você encontrará as fórmulas para calcular o ângulo entre dois vetores. Se você quiser entender como as derivamos, vá diretamente para o próximo parágrafo: como encontrar o ângulo entre dois vetores.

Ângulo entre dois vetores 2D

1. Vetores representados por coordenadas (notação sequenciada ordenada, forma retangular):

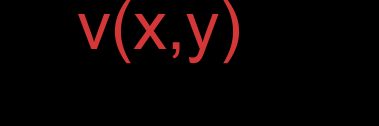
Para o vetor $\boldsymbol a$:

E $\boldsymbol b$:

O ângulo é:

2. Vetores entre um ponto inicial e um ponto final:

Para o vetor $\boldsymbol a$:

E:

Portanto, o vetor $\boldsymbol a$ é:

Para o vetor $\boldsymbol b$:

E:

Portanto, o vetor $\boldsymbol b$ é:

E:

Ângulo entre dois vetores 3D

1. Vetores representados por coordenadas:

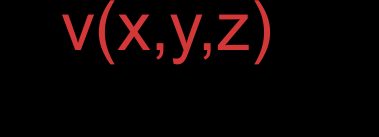
E:

Então:

2. Vetores entre um ponto inicial e um ponto final:

Para o vetor $\boldsymbol{a}$:

E:

Então:

Para o vetor $\boldsymbol{b}$:

E:

Então:

Encontre a fórmula final da mesma forma que para a versão 2D:

Além disso, é possível ter um vetor definido por coordenadas e o outro definido por um ponto inicial e terminal, mas não vamos deixar que isso obscureça ainda mais esta seção. Tudo o que importa é que a nossa calculadora de ângulo entre dois vetores tem todas as combinações possíveis disponíveis para você.

OK, o parágrafo acima foi um pouco longo demais. Para que você possa entender melhor as fórmulas do ângulo entre dois vetores, vamos verificar de onde elas vêm:

1. Comece com a fórmula geométrica básica para calcular o produto escalar 🇺🇸:

   O produto escalar é definido como o produto das magnitudes dos vetores multiplicado pelo cosseno do ângulo entre eles (aqui denotado por $\alpha$):

2. Em seguida, faça do ângulo o objeto da equação:

   Divida pelo produto das magnitudes dos vetores:

Encontre o arco cosseno:

3. Agora, precisamos revisar a definição da magnitude de um vetor:

   Como a magnitude é a raiz quadrada da soma dos componentes do vetor elevado à segunda potência, descobrimos que:

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2}$ no espaço 2D; e

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2+z^2}$ no espaço 3D.

Você notou que esta é a mesma fórmula usada na calculadora de distância? Esta fórmula vem diretamente da geometria! Aprenda mais sobre isso com a calculadora do teorema de Pitágoras.

4. Use a fórmula algébrica para o produto escalar (a soma dos produtos dos componentes dos vetores) e substitua as magnitudes:

No espaço 2D:

Se os vetores $\boldsymbol{a}$ e $\boldsymbol{b}$ forem, respectivamente:

E:

No espaço 3D:

Se os vetores $\boldsymbol{a}$ e $\boldsymbol{b}$ forem, respectivamente:

E:

Então:

E é isso!

Adicionalmente, se os vetores estiverem em uma forma diferente (e você conhece o ponto inicial e final), será necessário fazer alguns cálculos antes. O objetivo é reduzi-los à notação vetorial padrão.

Se o seu exemplo de vetor for descrito pelo ponto inicial $A=(x_1, y_1)$ e o ponto final $B=(x_2, y_2)$, então o vetor$\boldsymbol{a}$ pode ser expresso como:

Você ainda não está entendendo? Não se preocupe! Preparamos alguns exemplos para que você tenha certeza de que tudo está claro como um cristal.

Suponha que você queira encontrar o ângulo entre dois vetores:

e $\boldsymbol{b}$ é definido como o vetor entre o ponto $A = (1, 1, 2)$ e $B = (-4, -8, 6)$.

O que você precisa fazer?

1. Primeiro, calcule o vetor $\boldsymbol{b}$. Dados os pontos inicial e final:

2. Em seguida, encontre o produto escalar dos vetores $\boldsymbol{a}$ e $\boldsymbol{b}$:

3. Agora, determine a magnitude dos vetores:

E:

4. Por fim, use a equação do produto escalar:

Parabéns! Você acabou de calcular o ângulo entre dois vetores 3D.

Se você quiser aprender mais conceitos de geometria de coordenadas, recomendamos que consulte a calculadora da taxa média de variação.

Então, como funciona a nossa calculadora do ângulo entre dois vetores? Siga estas instruções passo a passo:

1. Escolha seu espaço vetorial. Vamos considerar o mesmo exemplo do parágrafo anterior. Nossos vetores e pontos têm três coordenadas, portanto, precisamos escolher a opção 3D.

2. Escolha a representação do primeiro vetor. O primeiro vetor está em notação padrão, portanto, deixamos o valor padrão: representação de coordenadas.

3. Insira o primeiro vetor. Digite $x = 3,$ $y = 6,$ e $z = 1$.

4. Escolha a representação do segundo vetor. Desta vez, precisamos alterá-la para representação de ponto.

5. Insira os valores do segundo vetor. Insira $\boldsymbol A = (1,1,2)$ e $\boldsymbol B = (-4,-8,6)$ nos campos apropriados.

6. A ferramenta encontrou o ângulo entre dois vetores 3D no momento em que você preencheu o último campo. No nosso caso, o resultado é $150{,}2\degree$, que é, obviamente, o mesmo resultado que obtivemos com os cálculos manuais.

Um vetor é um objeto geométrico que possui magnitude e direção. É muito comum usá-lo para representar quantidades físicas, como força, velocidade e deslocamento, entre outras.

O ângulo formado entre dois vetores é definido usando o arco cosseno dos produtos escalares dos dois vetores e o produto de suas magnitudes.

Para calcular o ângulo entre dois vetores em um espaço 2D:

1. Encontre o produto escalar dos vetores.
2. Divida o produto escalar pela magnitude do primeiro vetor.
3. Divida a resultante pela magnitude do segundo vetor.

Matematicamente, o ângulo α entre dois vetores [x_a, y_a] e [x_b, y_b] pode ser escrito como:

α = arccos[(x_a x_b + y_a y_b) / (√(x_a² + y_a²) × √(x_b² + y_b²))].

Para calcular o ângulo entre dois vetores em um espaço 3D:

1. Encontre o produto escalar dos vetores.
2. Divida o produto escalar pela magnitude do primeiro vetor.
3. Divida a resultante pela magnitude do segundo vetor.

Matematicamente, o ângulo α entre dois vetores [x_a, y_a, z_a] e [x_b, y_b, z_b] pode ser escrito como:

α = arccos[(x_a x_b + y_a y_b + z_a z_b) / (√(x_a² + y_a² + z_a²) × √(x_b² + y_b² + z_b²) )].