Calculadora da Taxa Média de Variação
Table of contents
O que é taxa de variação? Definição da taxa média de variaçãoFórmula da taxa média de variaçãoComo encontrar a taxa média de variação? Primeiro exemploComo encontrar a taxa média de variação? Segundo exemploFAQsA calculadora de taxa média de variação da Omni está aqui para ajudar você a entender o conceito simples escondido por trás de um nome longo e um pouco confuso. O que é a taxa de variação? De modo geral, ela mostra a relação entre dois fatores. Veja abaixo uma definição mais precisa da taxa média de variação. Também demonstraremos e explicaremos a fórmula da taxa média de variação com alguns exemplos de como você pode usá-la.
Você prefere assistir a ler? Aprenda tudo o que precisa em 90 segundos com este vídeo que fizemos para você:
O que é taxa de variação? Definição da taxa média de variação
Tudo está sempre em movimento. A mudança é inevitável. Começando com a aceleração de sua bicicleta ou carro, passando pelo crescimento populacional, do fluxo sanguíneo em suas veias até a simbiose de suas células, a taxa de variação nos permite estabelecer o valor associado a essas mudanças.
A taxa média de variação é uma taxa que descreve como um número muda, em média, em relação a outro. Se você tiver uma função, ela é a inclinação da reta traçada entre dois pontos. Mas não confunda isso com a inclinação. Você pode usar a taxa média de variação para qualquer função, não apenas para as funções lineares.
🙋 Se você quiser saber mais sobre inclinação, acesse a calculadora de inclinação da Omni.
Fórmula da taxa média de variação
Na figura a seguir, marcamos dois pontos para ajudar você a entender melhor como encontrar a taxa média de variação.
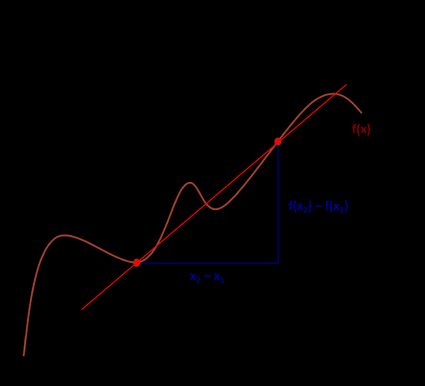
A fórmula da taxa média de variação é a seguinte:
A = [f(x₂) - f(x₁)] / [x₂ - x₁]
onde:
- (x₁, f(x₁)): coordenadas do primeiro ponto; e
- (x₂, f(x₂)): coordenadas do segundo ponto.
Se A for positivo, significa que um componente da coordenada aumenta à medida que o outro também aumenta. Por exemplo, quanto mais você anda de bicicleta, mais calorias você queima.
A é igual a zero quando um componente da coordenada muda, mas o outro não. Um bom exemplo pode ser o fato de você não estudar para as provas. Quando o tempo começa a se esgotar, a quantidade de coisas que você precisa aprender não muda.
A taxa média de variação A é negativa quando um componente da coordenada aumenta e a outro diminui. Digamos que você esteja saindo de férias. Quanto mais tempo você gasta na viagem, mais perto está do seu destino.
💡 Você pode aprender outras formas de descrever a diferença entre dois pontos na nossa calculadora de inclinação da reta 🇺🇸.
Como encontrar a taxa média de variação? Primeiro exemplo
Vamos calcular a taxa média de variação da distância (velocidade média) de um trem que vai de Paris a Roma (1420,6 km). No gráfico a seguir, você pode ver a mudança na distância ao longo do tempo:
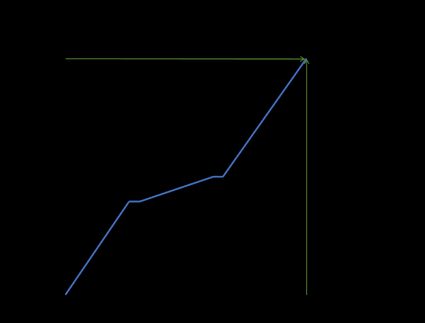
Como você pode ver, a velocidade não era constante. O trem parou duas vezes e, entre as paradas, foi significativamente mais lento. Mas para calcular a velocidade média, as únicas variáveis que importam são a mudança na distância e a mudança no tempo. Portanto, se as coordenadas do primeiro ponto são (0, 0) e as coordenadas do segundo ponto são (1420,6, 12,5), tratando-se da distância entre duas cidades e do tempo de viagem, respectivamente. Então, temos:
A = (1420,6 - 0) / (12,5 - 0) = 113,648 [km/h]
Em média, o trem estava a 113,648 quilômetros por hora. Agora, vamos dar uma olhada em um exemplo mais matemático.
Como encontrar a taxa média de variação? Segundo exemplo
Você tem a seguinte função:
f(x) = x² + 5x - 7
Encontre a taxa média de variação no intervalo [-4, 6].
-
Encontre os valores de sua função para ambos os pontos:
f(x₁) = f(-4) = (-4)² + 5(-4) - 7 = -11
f(x₂) = f(6) = 6² + (5 · 6) - 7 = 59
-
Use a equação da taxa média de variação:
A = [f(x₂) - f(x₁)] / [x₂ - x₁] = [f(6) - f(-4)] / [6 - (-4)] = [59 - (-11)] / [6 - (-4)] = 70 / 10 = 7
Se você gostou da calculadora de taxa média de variação, fique à vontade para conferir nossas outras ferramentas, como a calculadora de distância, na qual você pode encontrar a distância entre pontos ou retas.
A taxa média de variação é o mesmo que a inclinação?
Não necessariamente. A taxa média de variação reflete como uma função muda, em média, entre dois pontos. Por outro lado, definimos a inclinação de uma função como a inclinação da reta tangente à curva em um ponto específico. Em uma função linear, cada ponto muda de forma idêntica, de modo que a taxa média de variação e a inclinação são iguais.
Como encontrar a taxa média de variação de uma função?
Para encontrar a taxa média de variação de uma função, siga estas etapas:
-
Obtenha as coordenadas (x, y) do ponto inicial. Vamos chamá-las de (x₀, y₀).
-
Obtenha as coordenadas (x, y) do ponto final. Elas serão (x₁, y₁).
-
Substitua ambos na fórmula da taxa média de variação (A):
A = (y₁ - y₀)/(x₁ - x₀).
Qual é a taxa média de variação de y = 2x?
A taxa média de variação de y = 2x é 2. Como se trata de uma função linear, a taxa média de variação é apenas a inclinação da função. Nesse caso, para cada alteração na coordenada x, a coordenada y dobrará.
A velocidade é um exemplo de taxa média de variação?
Se a velocidade for constante, sim. A velocidade reflete como a posição muda instantaneamente em relação ao tempo. Portanto, se um objeto estivesse se movendo a uma velocidade constante, a taxa média de variação na posição nos diria a que velocidade ele está viajando.