Kalkulator przekątnej prostokąta

Nasz kalkulator przekątnej prostokąta to rozbudowane narzędzie, które szybko znajduje długość przekątnej i inne parametry prostokąta. Masz do czynienia z konkretnym problemem geometrycznym i nie wiesz, jak wyznaczyć przekątną prostokąta? Wpisz dane w pola naszego kalkulatora i poznaj rozwiązanie, lub przeczytaj poniższy tekst, aby dowiedzieć się, jakie są możliwe wzory na przekątną prostokąta.

Na poniższym rysunku możesz zobaczyć typowy prostokąt. Zaznaczyliśmy pięć podstawowych wielkości w tym prostokącie, które za chwilę wykorzystamy do wyprowadzenia wzoru na przekątną prostokąta. Są to:

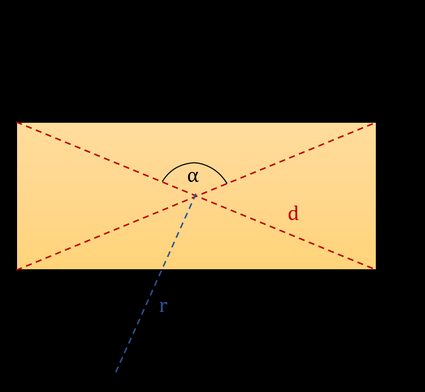
• l — długość,
• w — szerokość,
• α — kąt między przekątnymi,
• r — promień okręgu opisanego,
• d — przekątna,

oraz dwa inne parametry, które nie są pokazane na rysunku:

• P — powierzchnia, oraz
• Obw — obwód.

Określenie „prostokąt” pochodzi od łacińskiego „rectangulus”, który jest połączeniem dwóch słów: rectus (prawy, właściwy) i angulus (kąt). Nazwa ta wywodzi się z faktu, że prostokąt jest czworokątem o czterech kątach prostych (4 ⋅ 90° = 360°). Jego przeciwległe boki są równoległe do siebie i mają jednakową długość, a dwie przekątne przecinają się w środku i również mają jednakową długość.

Kwadrat jest szczególnym przypadkiem prostokąta. Jego definicja mówi, że ma wszystkie cztery boki równej długości lub ewentualnie, że kąt między jego przekątnymi jest prosty. Wypróbuj nasz kalkulator kwadratów 🇺🇸 — potrafi on szybko obliczać bok, obwód, pole i przekątną każdego kwadratu.

Środek prostokąta jest równomiernie oddalony od jego wierzchołków, dlatego można na nim zawsze opisać okrąg. Z drugiej strony, możemy wpisać okrąg w prostokąt tylko wtedy, gdy jest on kwadratem.

Aby wyznaczyć przekątną prostokąta, należy:

1. Zapisać boki prostokąta, które oznaczamy przez w i l.
2. Podnieść do kwadratu te dwie wartości, czyli obliczyć l² i w².
3. Dodać do siebie dwie podniesione do kwadratu wartości z kroku 2.
4. Obliczyć pierwiastek kwadratowy z otrzymanego wyniku.
5. Mamy to! Właśnie znalazłeś długość przekątnej swojego prostokąta.

Dlaczego ta metoda działa?

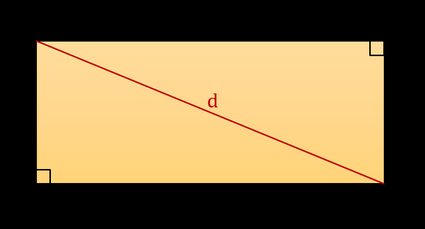
Aby wyznaczyć długość przekątnej prostokąta na podstawie wzoru użytego powyżej, podziel prostokąt na dwa przystające trójkąty prostokątne, czyli trójkąty zawierające kąt 90°. Każdy trójkąt będzie miał boki o długości l i w oraz przeciwprostokątną o długości d. Do wyznaczenia długości przekątnej prostokąta możesz wykorzystać wzór na przeciwprostokątną, np. z kalkulatora twierdzenia Pitagorasa. Ten wzór ma postać:

d² = l² + w².

Aby znaleźć przekątną prostokąta, wystarczy wziąć pierwiastek kwadratowy:

d = √(l² + w²).

Nasz kalkulator przekątnej prostokąta pozwala używać niemal dowolnych jednostek. Sprawdź nasz konwerter długości lub konwerter powierzchni 🇺🇸, aby dowiedzieć się, jak przełączać się pomiędzy różnymi jednostkami (układu SI i imperialnymi).

Czasami nie będziesz miał podanych długości dwóch sąsiednich boków prostokąta. Jak w takiej sytuacji znaleźć przekątną prostokąta? Odpowiedzi udzieli nasz kalkulator przekątnej prostokąta. Najpierw zapiszmy trzy podstawowe równania dla pola powierzchni, obwodu i promienia okręgu opisanego na prostokącie:

1. Powierzchnia prostokąta: P = w ⋅ l,
2. Obwód prostokąta: Obw = 2 ⋅ w + 2 ⋅ l,
3. Promień okręgu opisanego: r = d/2.

Mając powyższe równania, możemy teraz wyprowadzić różne wzory na przekątną prostokąta, które są wykorzystywane przez nasz kalkulator przekątnej prostokąta:

1. Znając długość i szerokość:
   d = √(l² + w²);

2. Znając jeden z boków i pole powierzchni:
   d = √(P²/l² + l²) lub
   d = √(P²/w² + w²),

3. Znając jeden z boków i obwód:
   d = √(2l² - Obw ⋅ l + Obw²/4)) lub
   d = √(2w² - Obw ⋅ w + Obw²/4),

4. Znając jeden z boków i kąt między przekątnymi:
   d = w / sin(α/2) lub
   d = l / cos(α/2),

5. Znając powierzchnię i obwód:
   d = ½√(Obw² - 8 ⋅ P),

6. Znając powierzchnię i kąt między przekątnymi:
   d = √(2 ⋅ P / sin(α)),

7. Znając obwód i kąt między przekątnymi:
   d = Obw / (2 ⋅ sin(α/2) + 2 ⋅ cos(α/2)),

8. Znając promień okręgu opisanego:
   d = 2 ⋅ r.

Uważaj: kąt α między przekątnymi znajduje się naprzeciwko boku określającego długość — jak na pierwszym rysunku. Pamiętaj też, że w kalkulatorze przekątnych prostokąta zakładamy, że długość jest większa od szerokości!

Czy wiesz, że istnieje specjalny prostokąt zwany złotym prostokątem? Jeśli nie, przejdź do naszego kalkulatora złotego prostokąta 🇺🇸, aby dowiedzieć się, jak można skonstruować złoty prostokąt!