Kalkulator obwodu figury
Dzięki naszemu kalkulatorowi obwodu figury nie musisz się już martwić o obliczenia związane z tym aspektem. Poniżej znajdziesz wzory na obwody dla dwunastu różnych kształtów, a także krótkie przypomnienie, czym właściwie jest obwód i jaka jest jego definicja. Czytaj dalej, wypróbuj go lub sprawdź brata bliźniaka tego kalkulatora — nasz wszechstronny kalkulator pola powierzchni.
Co to jest obwód?
Obwód to granica zamkniętej figury geometrycznej. Można go również zdefiniować jako zewnętrzną krawędź pola powierzchni, najdłuższą ciągłą linię otaczającą kształt. Sama nazwa pochodzi od greckiego perimetros: peri oznaczającego wokół i metros, rozumianego jako miara. Ponieważ jest to długość obrysu danego kształtu, wyraża się ją w jednostkach odległości — np. metrach, stopach, calach lub milach.
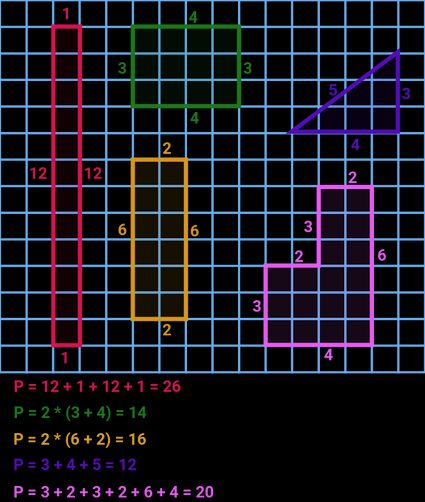
Jak znaleźć obwód — wzory na obwód
Zazwyczaj najprostszym i najlepszym podejściem jest znalezienie sumy wszystkich boków danego kształtu. Istnieją jednak przypadki, w których nie ma boków (takich jak elipsa, okrąg itp.) albo jeden, lub więcej boków jest nieznanych. W tym akapicie wymienimy wszystkie równania używane w naszym kalkulatorze obwodu figury.
Przewiń w dół do następnych sekcji, jeśli jesteś ciekawy/a konkretnego kształtu i chcesz zobaczyć wyjaśnienie, wyprowadzenie oraz wizualizacje dla każdego z dwunastu kształtów obecnych w tym kalkulatorze. Mamy również narzędzia dedykowane każdemu kształtowi — po prostu wpisz nazwę kształtu w pasku wyszukiwania u góry tej strony, a znajdziesz dedykowany kalkulator.
Poniżej znajdziesz wzory na obwód dla dwunastu figur geometrycznych przedstawionych w tym kalkulatorze:
-
Kwadrat — wzór na obwód: .
-
Wzór na obwód prostokąta: .
-
Wzór na obwód trójkąta:
-
Wzór na obwód koła:
-
Wzór na obwód wycinka okręgu: ( jest w stopniach)
-
Wzór na obwód elipsy:
-
Wzór na obwód czworokąta / trapezu:
-
Wzory na obwód równoległoboku:
-
Wzory na obwód rombu:
-
Wzór na obwód latawca:
-
Wzór na obwód pierścienia:
-
Wzór na obwód wielokąta foremnego:
Wzór na obwód kwadratu

Kwadrat ma cztery boki równej długości. Aby obliczyć jego obwód, wystarczy pomnożyć długość boku przez :
Mamy również kalkulator obwodu kwadratu 🇺🇸!
Wzór na obwód prostokąta

Wzór na obwód prostokąta jest prawie tak prosty, jak równanie na obwód kwadratu. Jedyna różnica polega na tym, że mamy dwie pary boków o równej długości:
Wzór na obwód trójkąta

Najprostszym wzorem na obliczenie obwodu trójkąta 🇺🇸 jest — jak zwykle — zsumowanie wszystkich boków:

Jednak nie zawsze masz podane trzy długości. Co możesz wtedy zrobić? Cóż, zamiast się denerwować, możesz użyć kalkulatora twierdzenia cosinusów 🇺🇸, aby znaleźć brakujący bok:
Można to uwzględnić we wzorze obwodu:

Inną opcją jest użycie twierdzenia sinusów, jeśli masz podany jeden bok oraz dwa kąty przylegające do tego boku:
oraz:
więc obwód trójkąta można wyrazić jako:
Wzór na obwód koła (wzór na obwód)

Obwód okręgu możesz sprawdzić w naszym kalkulatorze obwodu okręgu. Najbardziej znany wzór na obwód okręgu wykorzystuje tylko jedną zmienną — jego promień:
Czy kiedykolwiek zastanawiałeś/aś się, ile razy obróci się koło twojego roweru podczas dziesięciokilometrowej podróży? Cóż, jest to jeden z przypadków, w których będziesz musiał użyć wzoru na obwód okręgu. Wprowadź promień koła (połowę jego średnicy) i podziel dystans 10 kilometrów przez uzyskany obwód. Dla zwiększenia dokładności możesz uwzględnić rozmiar opony rowerowej.
Wzór na obwód wycinka okręgu

Obliczanie obwodu wycinka okręgu może wydawać się trudne — czy jest to tylko długość łuku, czy też długość łuku plus dwa promienie? Pamiętaj tylko o definicji obwodu! Obwód wycinka to suma długości wszystkich jego granic, a więc to drugie:
gdzie kąt jest podany w stopniach.
Wzór na obwód elipsy

Chociaż wzór na pole elipsy jest naprawdę prosty i łatwy do zapamiętania, wzór na obwód elipsy jest najbardziej kłopotliwy ze wszystkich równań wymienionych w naszym artykule. Zdecydowaliśmy się zaimplementować jedno z przybliżeń Ramanujana w tym kalkulatorze obwodu figury:
Gdzie jest najkrótszym promieniem, a najdłuższym możliwym promieniem elipsy. Inne, dokładniejsze przybliżenie Ramanujana to:
Istnieje również prostsza forma, wykorzystująca dodatkową zmienną :
To znaczy:
Możesz też skorzystać z naszego kalkulatora!
Wzór na obwód trapezu

Jeśli chcesz obliczyć obwód nieregularnego trapezu, nie ma specjalnego wzoru — po prostu dodaj wszystkie cztery boki:
Może zauważyłeś/aś, ale jest to wzór na każdy obwód czworokąta.
Istnieje również opcja, która pojawia się w przypadku niektórych specjalnych trapezów — takich jak trapez równoramienny, gdzie potrzebujesz znać długości boków , i . Innym przykładem jest trapez prosty, w którym długość podstaw i jednego ramienia wystarcza do znalezienia obwodu kształtu (aby znaleźć ostatnie ramię, obliczamy je z twierdzenia Pitagorasa).
Wzór na obwód równoległoboku

W naszym kalkulatorze obwodu znajdziesz trzy wzory do obliczania obwodu równoległoboku:
- Najprostszy, dodający wszystkie boki do siebie:

- Wzór na obwód równoległoboku, który wymaga podania długości jednego boku i przekątnych

- Obwód ze znanej podstawy, wysokości i dowolnego kąta równoległoboku.
Wzór na obwód rombu

Znalezienie wzoru na obwód rombu nie jest wielką filozofią, więc podsumujmy go zwięźle — jest taki sam jak wzór na obwód kwadratu!

Inny sposób na znalezienie obwodu rombu wymaga podania długości przekątnych:
Spróbuj samodzielnie wyprowadzić wzór. Wiesz, że dwie przekątne rombu są do siebie prostopadłe i przecinają się, więc możesz podzielić ten kształt na cztery przystające trójkąty prostokątne. Każdy trójkąt ma przyprostokątne o długościach e/2 i f/2 - wszystko, co musisz zrobić, to znaleźć przeciwprostokątną trójkąta, która jest jednocześnie bokiem rombu. Następnie pomnóż wynik przez cztery, aby znaleźć ostateczny obwód rombu.
Wzór na obwód latawca

Wzór na obwód latawca jest dość prosty — po prostu zsumuj wszystkie boki:
Wzór na obwód pierścienia

Ponieważ obwód jest zdefiniowany jako granica, pierścień wymaga dodania obwodu obu okręgów z których się składa:
Obwód wielokąta foremnego (pięciokąta foremnego, sześciokąta foremnego, ośmiokąta foremnego itp.)

W naszym kalkulatorze obwodu figury zaimplementowaliśmy również prosty wzór na obwód wielokąta foremnego:
gdzie to liczba boków wielokąta. Możesz więc na przykład obliczyć obwód pięciokąta, sześciokąta lub ośmiokąta.
Dodatkowo, dla wielokątów do 12 boków, nazwa wielokąta pojawi się w narzędziu. Super!
Jeśli chcesz określić obwód każdego wielokąta, zsumuj długości wszystkich jego boków:
gdzie , , ..., są długościami boków, a jest symbolem sumy (od do ).
Możesz też użyć współrzędnych wierzchołków:
Gdzie oraz .
FAQs
Jak obliczyć obwód nieregularnych kształtów?
Aby znaleźć obwód nieregularnej figury:
- Zmierz długości wszystkich (zewnętrznych) boków.
- Jeśli boki zawierają okrągłe fragmenty, zmierz promień i kąt środkowy, tj. kąt między promieniami, które łączą dwa punkty końcowe łuku ze środkiem.
- Zastosuj wzór na obwód okręgu dla tego promienia i weź część proporcjonalną do kąta.
- Dodaj do siebie długości wszystkich boków.
Czy mogę wyznaczyć pole powierzchni na podstawie obwodu?
Ogólnie rzecz biorąc, nie, nie jest możliwe obliczenie pola powierzchni na podstawie obwodu. Jest to szczególnie prawdziwe w przypadku prostokątów, równoległoboków, latawców i trapezów. Jednak w przypadku niektórych konkretnych kształtów, takich jak kwadraty, sześciokąty, wielokąty foremne i okręgi, możesz określić ich bok (promień w przypadku okręgów) na podstawie pola obwodu, a następnie obliczyć pole powierzchni.
Jaki jest obwód prostokątnego budynku o wymiarach 20 m na 15 m?
Obwód wynosi 70 m. Aby uzyskać ten wynik, musisz zsumować długości wszystkich czterech boków budynku. Dwa boki o długości 20 m dodane razem dają 40 m, podczas gdy pozostałe dwa boki o długości 15 m dodane razem dają 30 m. Razem otrzymujemy 40 m + 30 m = 70 m, zgodnie z twierdzeniem.