Calcolatore del Logaritmo

Questo calcolatore dei logaritmi ti consente di calcolare il logaritmo di un numero reale (positivo) in una base di tua scelta (positiva, diversa da 1). Indipendentemente dal fatto che tu stia cercando un logaritmo naturale, un logaritmo in base 2 o un logaritmo in base 10, questo strumento risolverà il tuo problema.

Continua a leggere per comprendere meglio la formula del logaritmo e le regole da seguire. Inoltre, potrai trovare alcune informazioni affascinanti, come il motivo per cui i logaritmi sono essenziali nella nostra vita e dove vengono applicati.

Se sei alla ricerca di altri utili calcolatori matematici, non esitare a dare un'occhiata al nostro calcolatore per la radice cubica, che ti permette di calcolare non solo la radice cubica ma anche le radici di qualsiasi indice.

Preferisci guardare piuttosto che leggere? Impara tutto ciò che ti serve in 90 secondi con questo video che abbiamo realizzato per te:

Una funzione logaritmica è l'inverso di una funzione esponenziale. In sostanza, se a elevato alla potenza y dà x, allora il logaritmo di x in base a è uguale a y. Sotto forma di equazioni, aʸ = x è equivalente a logₐ(x) = y.

In altre parole, il logaritmo di x, o logₐ(x), ci dice a quale potenza dobbiamo elevare a (o se x è maggiore di 1, quante volte a deve essere moltiplicato per se stesso) per ottenere il valore x. Da questo punto di vista, possiamo rappresentare il logaritmo anche nel modo seguente:

$a^{{\log}_a(x)} =x$

Speriamo che ora tu abbia capito la definizione di logaritmo; nella sezione seguente potrai leggere le due forme più utilizzate.

Puoi scegliere diversi numeri come base per i logaritmi; tuttavia, due basi particolari sono utilizzate così spesso che i matematici hanno dato loro nomi unici, il logaritmo naturale e il logaritmo decimale.

Logaritmo naturale

Se vuoi calcolare il logaritmo naturale di un numero, devi scegliere una base che sia approssimativamente uguale a 2,71828 1. Convenzionalmente questo numero è simboleggiato da e, dal nome di Leonard Euler, che ne definì il valore nel 1731. Di conseguenza, il logaritmo può essere rappresentato come logₑx, ma tradizionalmente viene indicato con il simbolo ln(x). Potresti anche vedere log(x), che si riferisce alla stessa funzione, soprattutto in finanza e in economia. Pertanto, y = logₑx = ln(x) che è equivalente a x = eʸ = exp(y).

Un modo pratico per comprendere la funzione del logaritmo naturale è quello di inserirlo nel contesto degli interessi composti. Un interesse composto viene calcolato sia sul capitale che sugli interessi accumulati.

La formula dell'interesse composto annuale è la seguente:

A = P(1 + r/m)ᵐᵗ,

dove:

• A è il valore dell'investimento dopo t anni;
• P è il valore iniziale;
• r è il tasso di interesse annuale (in decimali);
• m rappresenta il numero di volte in cui l'interesse viene composto all'anno o la frequenza di composizione; e
• t si riferisce al numero di anni.

Supponiamo di depositare del denaro per un anno in una banca in cui la composizione è frequente, quindi m è un numero elevato. È facile vedere come il valore di m aumenti rapidamente se si confrontano le frequenze annuali (m=1), mensili (m=12), giornaliere (m=365) o orarie (m=8,760). Ora, immaginiamo che il denaro venga ricalcolato ogni minuto o secondo: m diventerà un numero considerevolmente alto.

Ora verifichiamo come la frequenza crescente influisce sul tuo denaro iniziale:

Potrai notare che, anche se la frequenza della capitalizzazione raggiunge un numero insolitamente alto, il valore di (1 + r/m)ᵐ (che è il moltiplicatore del tuo deposito iniziale) non aumenta molto. Al contrario, diventa piuttosto stabile: si avvicina a un valore unico già menzionato in precedenza, e ≈ 2,71828 1.

Poiché i tassi di crescita seguono spesso uno schema simile a quello dell'esempio precedente, anche l'economia si basa molto sui logaritmi naturali. Due variabili comuni coinvolgono il logaritmo naturale: il tasso di crescita del PIL 🇺🇸 e l'elasticità della domanda al prezzo.

Logaritmo decimale

L'altra forma popolare di logaritmo è il logaritmo decimale in base 10, log₁₀x, convenzionalmente indicato come lg(x). È noto anche come logaritmo volgare, logaritmo decadico, logaritmo standard o logaritmo Briggsiano, dal nome di Henry Briggs, un matematico inglese che ne sviluppò l'uso.

Come suggerisce il nome, è la forma di logaritmo più semplice. Viene utilizzata, ad esempio, nel nostro calcolatore di decibel. Le tavole dei logaritmi che in passato avevano lo scopo di facilitare i calcoli presentavano anche i logaritmi comuni.

La tabella seguente rappresenta alcuni logaritmi comuni e naturali frequenti.

Se vuoi calcolare un logaritmo in una base arbitraria, ma puoi usare solo una calcolatrice per logaritmi naturali o a una calcolatrice per logaritmi in base 10, devi applicare le seguenti regole:

• logₐ(x) = ln(x)/ln(a), e
• logₐ(x) = lg(x)/lg(a).

Supponiamo che tu voglia usare questo strumento come calcolatore di logaritmi in base 2. Per calcolare il logaritmo di qualsiasi numero, segui questi semplici passaggi:

1. Decidi il numero di cui vuoi trovare il logaritmo. Supponiamo che sia 100;
2. Decidi la tua base - in questo caso, 2.
3. Trova il logaritmo in base 10 del numero 100: lg(100) = 2;
4. Trova il logaritmo in base 10 del numero 2: lg(2) = 0,30103;
5. Dividi questi valori tra loro: lg(100) / lg(2) = 2 / 0,30103 = 6,644; e
6. Puoi anche saltare i passaggi 3-5 e inserire il numero e la base direttamente nella calcolatore per i logaritmi.

Le prove suggeriscono che il concetto di logaritmo era già noto nell'India dell'VIII secolo. Tuttavia, il concetto sviluppato di logaritmo apparve per la prima volta nel libro intitolato Mirifici logarithmorum canonis descriptio (la costruzione del meraviglioso canone dei logaritmi) stampato nel 1614. Si trattava del risultato di 20 anni di ricerche del matematico scozzese John Napier, che mirava a semplificare i calcoli per le sue altre necessità di astronomo e fisico.

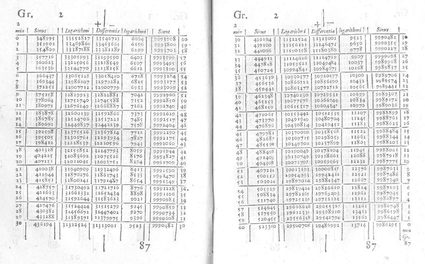
La prima parte del libro spiega con precisione la teoria del logaritmo, le sue proprietà e le sue aree di applicazione. La seconda parte del libro propone esempi di calcoli logaritmici mediante novanta pagine di tavole. Napier enuncia anche i limiti del suo lavoro e fornisce analogie, esempi, avvertimenti, promemoria e conclusioni. Per questo motivo il libro può funzionare come un manuale di istruzioni. Lo scienziato, tuttavia, non fornisce dettagli su come abbia creato questo formidabile strumento.

La nostra generazione, a prima vista potrebbe non apprezzare facilmente l'invenzione del logaritmo, dal momento che abbiamo sempre usato moderni calcolatrici e computer per i calcoli matematici. Tuttavia, nel XVII secolo come calcolare i logaritmi fu una scoperta che ebbe un impatto profondo sulla vita delle persone. Prima della comparsa dei logaritmi, risolvere i problemi matematici poteva richiedere ore, giorni o addirittura anni.

Il primo progresso esplicito apportato dai logaritmi fu la semplificazione dei calcoli grazie alla conversione di moltiplicazioni e divisioni in addizioni e sottrazioni. L'unico sforzo richiesto consisteva nel cercare logaritmi e antilogaritmi nelle tabelle.

Il nuovo metodo di calcolo fu fondamentale nel campo dell'astronomia. Le attività scientifiche di Napier coincisero con un'era di nuovi sviluppi dell'astrofisica. Di conseguenza, molti astronomi erano alle prese con eterni calcoli per individuare la posizione dei pianeti in base alla teoria del sistema solare di Copernico. Johannes Kepler, che all'epoca lavorava alle sue famose leggi sui moti planetari, era tra questi.

Grazie all'impresa di Napier, Keplero poté ridurre notevolmente il suo carico di lavoro, che in precedenza richiedeva quasi mille pagine di calcoli, permettendogli di dedicare più tempo alle speculazioni filosofiche.

Il famoso matematico britannico Henry Briggs si rese subito conto delle capacità della nuova invenzione e si trasferì in Scozia per incontrare Napier e iniziare a cercare insieme potenziali sviluppi.

Dopo aver modificato l'idea originale, nel 1617 i due formularono la prima tabella dei logaritmi basata sulle potenze di 10. Nel 1624, dopo la morte di Napier, Briggs pubblicò il suo libro Arithmetica logarithmic che presentava le tavole logaritmiche per trentamila numeri naturali con 14 cifre decimali. Questa forma di logaritmi è chiamata oggi forma volgare de logaritmi. (Katrici, 2007)

La crescente popolarità di questo nuovo strumento matematico stimolò ulteriori sviluppi. Nel 1620 Edmund Gunter introdusse la linea calcolatrice del logaritmo, un dispositivo fisico utilizzato per le moltiplicazioni e le divisioni.

La prima versione dello strumento richiedeva un paio di bussole per la misurazione e fu migliorata da William Oughtred intorno al 1622. Egli progettò il convenzionale regolo scorrevole, un dispositivo con due righelli che scorrevano l'uno accanto all'altro.

In questo modo, Oughtred creò un nuovo approccio che facilitò ulteriormente il calcolo della legge del logaritmo. I regoli calcolatori divennero uno strumento di calcolo comune nelle professioni che richiedevano l'aritmetica. Architetti, ingegneri, scienziati e persino astronauti si sono affidati a questo calcolatore fino all'avvento della rivoluzione digitale. Albert Einstein ne utilizzava uno e gli equipaggi delle missioni Apollo portarono i regoli calcolatori perfino nello spazio.

Rispetto alle prime versioni dei computer, il regolo calcolatore aveva molti vantaggi:

• È abbastanza piccolo da poter essere tenuto in tasca;
• Non richiede una fonte di alimentazione;
• È relativamente economico;
• È meccanicamente affidabile;
• È semplice da usare; e
• Può risolvere qualsiasi problema numerico in situazioni ordinarie.

Al giorno d'oggi, i moderni computer e le calcolatrici scientifiche hanno sostituito pratiche antiquate. Tuttavia, comprendere i concetti alla base dei logaritmi può aiutarti a sviluppare le tue abilità matematiche. I logaritmi hanno molteplici usi pratici in molti campi.

Il fatto che i logaritmi mettano in relazione la progressione aritmetica con la progressione geometrica suggerisce che alcuni fenomeni del mondo reale potrebbero formare un modello logaritmico. In effetti, ci sono molti esempi in natura e nella nostra vita pratica che possono essere attribuiti al magico logaritmo.

Ad esempio, i seguenti fenomeni naturali rappresentano una spirale logaritmica:

• Guscio di un nautilus

• Galassie

• Cicloni

Inoltre, ci sono altri fenomeni che vengono misurati sulla scala logaritmica:

• Durezza dei minerali — Scala di Mohs;
• Intensità dei suoni — Decibel (dB);
• Intensità del vento — Scala di Beaufort;
• Terremoti — Scala Richter; e
• Acidità — pH.

💡 Sapevi che il logaritmo aiuta a calcolare il valore della cifra di rumore 🇺🇸, che è importante nelle aree di studio della riduzione e del controllo del rumore.

Prima della fine degli anni '70, quando le calcolatrici tascabili divennero accessibili al pubblico normale, l'esecuzione di calcoli, soprattutto con le frazioni, richiedeva un notevole sforzo manuale. Per alleviare questo noioso lavoro, l'applicazione dei logaritmi aveva una funzione pratica.

Per sfruttare i vantaggi tecnici del logaritmo, dobbiamo conoscere le sue proprietà di base. Presumibilmente le conosci già ma, per ricordartelo, la tabella che segue te le mostra.

Per dimostrare quanto fosse utile nell'era pre-calcolatrice, supponiamo di dover calcolare il prodotto di 5,89 × 4,73 senza alcun dispositivo elettronico. Potreste farlo semplicemente moltiplicando su carta, ma ci vorrebbe un po' di tempo. Si può invece utilizzare la regola del logaritmo con le tavole dei logaritmi e ottenere un'approssimazione relativamente buona del risultato.

Se si disponesse di una tavola dei log, si potrebbe verificare rapidamente il logaritmo di questi numeri (oppure si potrebbe usare Internet per trovare una tavola online), ma imbrogliamo un po' e usiamo il nostro calcolatore allo scopo.

$\text{lg}(5,\!89) ≅ 0,77011\:53$ e $\text{lg}(4,\!73) ≅ 0,\!67486\:1$

Applicando la prima regola possiamo riscrivere la seguente equazione:

$\text{lg}(5,\!89 \times 4,\!73) =\text{lg}(5,\!89) + \text{lg}(4,\!73) ≅ 0,\!77011\:5 + 0,\!67486\:11$

$\text{lg}(5,\!89 \times 4,\!73) ≅ 1,\!44497\:61$

Non sappiamo ancora quale sia il risultato esatto, quindi prendiamo l'esponente di entrambi i lati dell'equazione precedente con qualche modifica sul lato destro.

$5,\!89 \times 4,\!73 ≅ 10^{1,44497\:61} = 10^{0,44497\:61} \times 10^1$

Ora è necessario verificare 10^0,4449761 in una tavola degli antilogaritmi o, in alternativa, controllare con il nostro calcolatore per l'antilogaritmo. Qual è l'antilogaritmo di 0,4449761 in base 10? 2,785968.

Riscrivendo l'equazione:

$5,\!89 \times 4,\!73 ≅ 2,\!78596\:8 \times 10^1 = 27,\!85968$

Probabilmente la procedura sopra descritta sembra impegnativa rispetto a comporre l'operazione iniziale su di una calcolatrice tascabile o all'utilizzo di un'applicazione capace come il nostro calcolatore. Per mostrare come il potere dei logaritmi possa aiutarti anche nei tempi moderni, consideriamo un operazione fattoriale 🇺🇸 di 100, che è il prodotto di tutti i numeri interi da 1 a 100.

$100! = 1 \times 2 \times 3 \times 4 \times ⋯ \times 99 \times 100$

Se si cercasse di risolvere questo problema con una normale calcolatrice tascabile, probabilmente si fallirebbe, poiché il risultato è un numero enorme con molte cifre.

Ma con l'aiuto di algoritmi, è possibile riscrivere (con qualche arrotondamento) l'operazione come:

$\text{lg100!} = \text{lg1} + \text{lg2} + \text{lg3} + ⋯ + \text{lg100} = 0 + 0,\!30103 + 0,\!47712 + ⋯ + 2 ≅ 157,\!97$

$100! ≅ 10^{0,97} \times 10^{157} = 9,\!3325 \times 10^{157}$

Intelligente, vero?