Calcolatore per l'Altezza del Triangolo
Il calcolatore per l'altezza del triangolo è lo strumento perfetto per trovare le lunghezze delle altezze di un triangolo qualsiasi. Qui potrai calcolare tutte le altezze di un triangolo scaleno, isoscele, equilatero o rettangolo.
Oltre alle altezze, questo calcolatore è in grado di trovare altri parametri relativi al tuo triangolo, come i lati, gli angoli, il perimetro e l'area.
Continua a leggere quest'articolo per ottenere le risposte alle seguenti domande:
- Qual è la definizione dell'altezza di un triangolo?
- Qual è la formula dell'altezza di un triangolo? (Ce ne sono diverse!)
- Come si calcola l'altezza di un triangolo equilatero?
- Come trovare l'altezza di un triangolo isoscele con o senza area?
- Come trovare l'altezza di un triangolo rettangolo?
- Come si calcola l'altezza di un triangolo usando il calcolatore per l'altezza del triangolo?
Inoltre, nella sezione FAQ troverai le risposte ad altre domande concenti, per esempio: come si calcola l'altezza relativa al lato obliquo di un triangolo isoscele? e quante altezze ha un triangolo?
Si parte!
Che cos'è l'altezza di un triangolo?
Per definizione, l'altezza di un triangolo è una linea perpendicolare a uno dei lati tracciata dal vertice opposto. Ogni triangolo ne ha tre, perché è possibile tracciare un'altezza da ognuno dei tre lati del triangolo.
Due delle tre altezze di un triangolo isoscele sono uguali, mentre in un triangolo equilatero, le altezze sono tutte uguali. Usa il calcolatore per l'altezza del triangolo per vedere con i tuoi occhi!
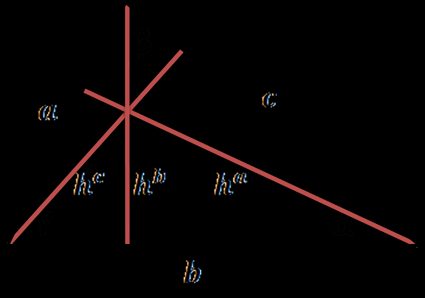
Formula dell'altezza di un triangolo: come si calcola l'altezza di un triangolo?
Ci sono molti modi per trovare l'altezza di un triangolo. Il più usato è quello che utilizza l'area del triangolo, ma esistono molte altre formule.
-
Data l'area del triangolo
Per ricavare questa formula elementare per l'altezza di un triangolo, basta trasformare la formula dell'area che conosciamo tutti:
dove:
-
— Base; e
-
— Altezza.
Quindi:
-
Ma come trovare l'altezza di un triangolo scaleno senza area? In questo caso, dovrai usare altre formule per l'altezza di un triangolo. Vediamole insieme.
-
Dati i lati del triangolo
La formula per altezza di un triangolo date le lunghezze dei lati usa la formula di Erone, per poi trasformarla utilizzando la formula per l'area che abbiamo visto prima. In poche parole, l'equazione risultante calcola l'area e le altezze simultaneamente.
Ecco la formula di Erone:
Pertanto, possiamo introdurre la formula dell'area per ricavare la formula dell'altezza del triangolo:
Per saperne di più su questa equazione, puoi consultare il nostro calcolatore per la formula di Erone 🇺🇸.
-
Dati due lati e l'angolo tra di essi
Questa volta, utilizzeremo la trigonometria per trovare l'area:
oppure
oppure
Utilizza la formula appropriata a seconda dei lati dati.
Quindi, possiamo ricavare la formula dell'altezza del triangolo:
Come abbiamo visto nella prima figura, in queste formule, l'angolo α è opposto al lato a, l'angolo β è opposto al lato b, e l'angolo γ è opposto al lato c.
Queste erano le formule per calcolare l'altezza di un triangolo scaleno, quindi qualsiasi triangolo. Ma non è finita qui! Adesso vedremo come trovare l'altezza di un triangolo equilatero, isoscele e rettangolo. Queste versioni sono più facili perché prendono delle scorciatoie.
Come si calcola l'altezza di un triangolo equilatero?
Adesso scoprirai come si trova l'altezza di un triangolo equilatero! Emozionante, vero?
Un triangolo equilatero è un triangolo i cui angoli e lati sono uguali. In particolare, gli angoli sono pari a . Perciò, anche le tre altezze hanno la stessa lunghezza. Se utilizzi il nostro calcolatore per l'altezza del triangolo, vedrai che tutto quello che devi inserire è la lunghezza del lato.
Vediamo la formula dell'altezza di un triangolo equilatero:
-
dove:
- — Lato del triangolo equilatero.
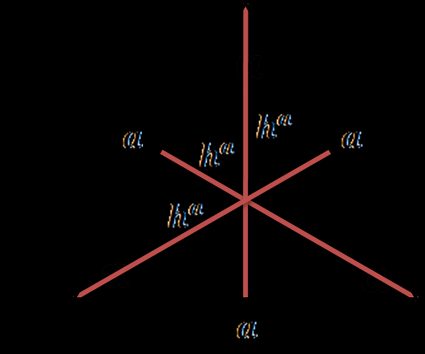
In un triangolo equilatero, le altezze, le bisettrici degli angoli, le bisettrici delle perpendicolari e le mediane coincidono.
Se ti interessano le formule per l'area e il perimetro di un triangolo equilatero, consulta il nostro calcolatore per il triangolo equilatero.
Come si calcola l'altezza di un triangolo isoscele?
Un triangolo isoscele è un triangolo con due lati uguali; perciò, le altezze tracciate dagli angoli alla base sono uguali, mentre la terza è tracciata dall'angolo al vertice.
Come trovare l'altezza relativa alla base di un triangolo isoscele senza area?
-
dove:
-
— Lunghezza del lato obliquo; e
-
— Base.
Questa formula dell'altezza del triangolo isoscele deriva dal teorema di Pitagora.
-
Come si calcola la lunghezza dell'altezza relativa al lato obliquo di un triangolo isoscele?
Puoi utilizzare la formula con l'area:
O la trigonometria:
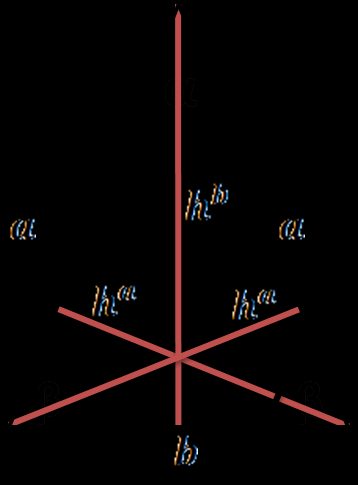
Per le formule dell'area e del perimetro di questo tipo di triangolo, visita il nostro calcolatore per il triangolo isoscele.
Come trovare l'altezza di un triangolo rettangolo?
La formula per calcolare due delle tre altezze di un triangolo rettangolo sono molto facile: basta determinare le lunghezze dei cateti, ovvero dei lati adiacenti all'angolo retto, e il gioco è fatto!
Invece, usa la formula seguente per trovare la terza altezza del triangolo rettangolo, tracciata dall'angolo retto:

Se le equazioni dell'area e del perimetro di questo triangolo ti interessano, consulta il nostro calcolatore per il triangolo rettangolo.
Come si trova l'altezza di un triangolo con questo calcolatore per l'altezza del triangolo?
Dopo aver letto la nostra spiegazione, siamo sicuri che ora hai capito che cos'è l'altezza di un triangolo e come trovare l'altezza di un triangolo senza l'area. Ma vediamo un semplice esempio per mostrarti la flessibilità del nostro strumento:
- Scegli il tipo di triangolo. Supponiamo di voler calcolare l'altezza di un triangolo scaleno, quindi non cambiamo l'opzione predefinita;
- Inserisci i parametri noti, per esempio, le lunghezze dei tre lati, o due lati e l'angolo tra essi. Rimaniamo sulla prima opzione, quindi inserisci , , ; e infine
- Il calcolatore per l'altezza del triangolo ti mostrerà le lunghezze delle altezze: , , e . Inoltre, scoprirai le misure di tutti gli angoli, l'area e il perimetro del triangolo.
Non è fantastico?
FAQs
Come si calcola l'altezza relativa al lato obliquo di un triangolo isoscele?
Se vuoi trovare l'altezza relativa al lato obliquo di un triangolo isoscele, dovrai seguire questi passaggi:
-
Moltiplica l'area per 2;
-
Dividi il risultato per la misura del lato obliquo; e
-
Il gioco è fatto! La formula completa è:
Altezzaobliquo = 2 × area / lato obliquoSe vuoi calcolare l'altezza relativa al lato obliquo di un triangolo isoscele senza l'area, dovrai utilizzare quest'altra formula:
Altezzaobliquo = √[a2 − (base / 2)2] × base / lato obliquo
Oppure la trigonometria:
Altezzaobliquo = base × sin(β)
dove:
- β — Angolo alla base.
Quante altezze ha un triangolo?
Ogni triangolo ha tre altezze. Questo è dovuto al fatto che i triangoli hanno tre lati e tre vertici, e per definizione dell'altezza di un triangolo, da ogni lato può essere tracciata un'altezza al vertice opposto.
Come trovare l'altezza di un triangolo isoscele senza area?
Per calcolare l'altezza relativa alla base di un triangolo isoscele, cioè l'altezza tracciata dal vertice, segui questi passaggi:
-
Dividi la lunghezza della base per 2;
-
Eleva il risultato al quadrato;
-
Sottrai il risultato del passaggio 2 dal quadrato della lunghezza del lato obliquo; e
-
Prendi la radice quadrata del risultato ottenuto. La formula completa è la seguente:
Altezzabase = √[a2 − (b / 2)2]
Come trovare l'altezza di un triangolo rettangolo?
Ogni cateto di un triangolo rettangolo è anche una delle sue altezze. Per calcolare la terza altezza, h3, devi usare due formule dell'area contemporaneamente:
Area = cateto1 × cateto2 / 2 = ipotenusa × h3 / 2
Di conseguenza:
h3 = cateto1 × cateto2 / ipotenusa
Come trovare l'altezza di un triangolo ottusangolo?
Benché due delle tre altezze di un triangolo ottusangolo si trovino all'esterno del triangolo, il calcolo delle loro misure è uguale a tutti gli altri triangoli. Devi semplicemente moltiplicare l'area per 2, e dividere il risultato per la lunghezza del lato a cui è relativa l'altezza ricercata:
Altezzaa = area × 2 / a