Calcolatore per il Triangolo Rettangolo

Il calcolatore per il triangolo rettangolo ti aiuterà a trovare la lunghezza dei lati di un triangolo rettangolo. Questo calcolatore per il triangolo rettangolo ti insegnerà anche a trovare l'area di un triangolo rettangolo e ti darà molte informazioni sugli usi pratici del triangolo rettangolo.

Prima di tutto, spieghiamo cos'è un triangolo rettangolo. La definizione è molto semplice e potrebbe sembrare ovvia per chi la conosce già — Un triangolo rettangolo è un triangolo in cui uno e uno solo degli angoli è esattamente di 90°. Gli altri due angoli saranno chiaramente più piccoli dell'angolo retto perché la somma di tutti gli angoli di un triangolo è sempre 180°.

In un triangolo rettangolo, definiamo i lati in modo particolare. Il lato opposto all'angolo retto è sempre il più grande del triangolo e prende il nome di "ipotenusa". Gli altri due lati sono chiamati cateti. La relazione tra l'ipotenusa e ogni cateto è semplice, come vedremo quando parleremo del teorema di Pitagora.

Se vuoi calcolare solo l'ipotenusa di un triangolo rettangolo, questa pagina e il suo calcolatore per il triangolo rettangolo sarà molto utile. Tuttavia, ti consigliamo di utilizzare anche lo strumento dedicato che abbiamo sviluppato su Omni — calcolatore per l'ipotenusa. L'ipotenusa è opposta all'angolo retto e può essere risolta utilizzando il teorema di Pitagora. In un triangolo rettangolo con cateti a e b e con ipotenusa c, il teorema di Pitagora afferma che — a² + b² = c².

Per risolvere c, prendi la radice quadrata di entrambi i lati per ottenere c = √(b² + a²). Possiamo considerare questa estensione del teorema di Pitagora come una "formula dell'ipotenusa". Il calcolatore per il teorema di Pitagora è un ottimo strumento per calcolare l'ipotenusa.

Risolviamo ora un esempio pratico di calcolo dell'ipotenusa di un triangolo rettangolo senza utilizzare i calcolatori disponibili su Omni:

1. Ottieni i valori di a e b;
2. Eleva al quadrato a e b;
3. Somma i due valori: a² + b²;
4. Prendi la radice quadrata del risultato;
5. La radice quadrata darà risultati positivi e negativi. Dato che si tratta di una lunghezza, non tenere conto del risultato negativo; e
6. Il valore risultante è il valore dell'ipotenusa c.

Vediamo ora quale sarebbe il procedimento utilizzando uno dei calcolatori di Omni, ad esempio il calcolatore per triangoli rettangoli presente in questa pagina web:

1. Inserisci i valori di a e b nel calcolatore;
2. Ottieni immediatamente il valore di c; e
3. Come bonus, otterrai il valore dell'area di questo triangolo.

Abbiamo già visto che calcolare l'area di un triangolo rettangolo è molto facile con il calcolatore per il triangolo rettangolo. In Omni, abbiamo un calcolatore specificamente progettata per questo scopo — calcolatore per l'area del triangolo rettangolo. Vediamo ora in modo un po' più approfondito come calcolare l'area dei triangoli rettangoli.

Il metodo per trovare l'area di un triangolo rettangolo è piuttosto semplice. Tutto ciò di cui hai bisogno sono le lunghezze della base e dell'altezza. In un triangolo rettangolo, la base e l'altezza sono i due lati che formano l'angolo retto. Poiché moltiplicando questi due valori si ottiene l'area del rettangolo corrispondente, e il triangolo è la metà di questo, la formula è la seguente:

Area = ½ × base × altezza.

Se non conosci la base o l'altezza, puoi trovarle utilizzando il teorema di Pitagora. Prova il calcolatore per il triangolo rettangolo per verificare i tuoi calcoli o calcola l'area di triangoli con lati di lunghezza maggiore o con valori decimali.

Ora vedremo altre cose che possono essere calcolate a partire da un triangolo rettangolo utilizzando alcuni degli strumenti disponibili su Omni. I lati di un triangolo hanno una certa pendenza. La formula della pendenza è

Pendenza = (y₂ - y₁)/(x₂ - x₁).

Quindi se le coordinate sono (1, -6) e (4, 8), la pendenza del segmento è (8 + 6)/(4 - 1) = 14/3. Un modo semplice per determinare se il triangolo è retto, conoscendo solo le coordinate, è quello di vedere se le pendenze di due linee si moltiplicano fino a diventare -1.

Esiste un modo semplice per convertire gli angoli da radianti a gradi e da gradi a radianti utilizzando la conversione degli angoli:

• Se un angolo è in radianti — moltiplicalo per 180/π; e
• Se un angolo è in gradi, moltiplicalo per π/180.

A volte puoi incontrare un problema in cui mancano due o addirittura tre lunghezze di lati. In questi casi, il calcolatore per il triangolo rettangolo, il calcolatore per l'ipotenusa e il metodo per trovare l'area di un triangolo rettangolo non ti saranno d'aiuto. Devi utilizzare le funzioni trigonometriche per risolvere i pezzi mancanti.

Il triangolo rettangolo è solo uno dei tanti triangoli speciali che esistono. Questi triangoli hanno una o più caratteristiche speciali che li rendono unici. Ad esempio, come abbiamo visto, il triangolo rettangolo ha un angolo retto e quindi un'ipotenusa, il che lo rende un triangolo unico. Oltre al triangolo rettangolo, esistono altri triangoli speciali con proprietà interessanti.

Uno dei triangoli speciali più conosciuti è il triangolo equilatero, che ha tre lati uguali e tutti i suoi angoli sono di 60°. Per questo motivo è molto più semplice creare un calcolatore per la risoluzione dei triangoli che valuti i diversi parametri di un triangolo di questo tipo.

Un altro triangolo speciale è il triangolo isoscele, che ha due lati di uguale lunghezza e quindi due angoli della stessa misura. A differenza del triangolo equilatero, i triangoli isosceli hanno molte forme diverse.

Esistono molti altri triangoli speciali. Tuttavia, ora daremo un'occhiata ad alcuni triangoli rettangoli molto speciali che, oltre ad essere triangoli rettangoli, hanno altre proprietà uniche che li rendono interessanti.

Il cosiddetto triangolo "45 45 90" è probabilmente il più speciale tra tutti i triangoli rettangoli speciali. Si tratta di un triangolo rettangolo che è anche un triangolo isoscele. Entrambi i suoi cateti sono della stessa lunghezza (isosceli) e ha anche la particolarità che gli angoli non retti sono esattamente la metà dell'angolo retto che dà il nome al triangolo rettangolo.

Questo triangolo rettangolo è il tipo di triangolo che si ottiene quando dividi un quadrato per la sua diagonale. Per questo motivo entrambi i cateti (lati del quadrato) sono di uguale lunghezza. Se vuoi saperne ancora sul più speciale dei triangoli rettangoli, consigliamo di consultare il calcolatore per triangoli 45 45 90 creato a questo scopo.

Un altro affascinante triangolo del gruppo dei triangoli rettangoli speciali è il cosiddetto triangolo "30 60 90". Il nome deriva dal fatto che ha un angolo retto (90°), poi un angolo di 30° e un altro di 60°. Questi angoli sono speciali a causa dei valori delle loro funzioni trigonometriche (coseno, seno, tangente, etc.). Le conseguenze di ciò possono essere viste e comprese con il calcolatore per triangoli 30 60 90, ma per coloro che sono troppo pigri per cliccare sul link, riassumeremo qui alcune di esse. Supponendo che il lato minore sia di lunghezza a, il triangolo è il seguente:

1. La seconda lunghezza è uguale a a√3;
2. L'ipotenusa è 2a;
3. L'area è uguale a (a²√3)/2; e
4. Il perimetro è uguale a a(3 + √3).

A prima vista potrebbe sembrare che un triangolo rettangolo e un parallelogramma non abbiano nulla in comune. Come può un risolutore di triangoli aiutarti a comprendere un parallelogramma? La realtà è che qualsiasi parallelogramma può essere scomposto in 2 o più triangoli rettangoli. Facciamo l'esempio del rettangolo, che è il più semplice da capire.

Immagina un rettangolo, un rettangolo qualsiasi. Ora traccia una linea su una delle diagonali di questo rettangolo. Se separiamo il rettangolo dalla diagonale, otterremo due triangoli rettangoli. Osservando i triangoli, non c'è bisogno di usare il calcolatore per triangoli rettangoli per vedere che entrambi sono uguali, quindi le loro aree saranno uguali. Ciò significa che l'area del rettangolo è il doppio di quella di ciascun triangolo.

Se pensiamo alle equazioni, questo ha senso perché l'area di un rettangolo di lati a e b è esattamente area = a × b, mentre per il triangolo rettangolo è area = base × altezza / 2 che, in questo caso, significherebbe area = a × b / 2. Questo è esattamente ciò che abbiamo già visto tagliando il rettangolo per la diagonale.

Era un semplice esempio di rettangolo, ma lo stesso vale per l'area di un quadrato. Per altri parallelogrammi, il procedimento diventa un po' più complicato (potrebbe coinvolgere fino a 4 triangoli rettangoli di dimensioni diverse). Tuttavia, con un po' di abilità, puoi utilizzare la stessa idea e calcolare l'area di un parallelogramma utilizzando i triangoli rettangoli. Naturalmente puoi essere ancora più efficiente e utilizzare il nostro calcolatore.

La geometria e i poligoni, in particolare i triangoli, sono sempre in sintonia. Le proprietà di alcuni triangoli, come i triangoli rettangoli, sono solitamente interessanti e sconvolgenti, anche per i non matematici. Ora daremo un'occhiata a un interessante insieme di numeri strettamente correlati ai triangoli rettangoli che i matematici amano e che forse piacerà anche a te.

Questi insiemi di numeri sono chiamati terne pitagoriche e sono insiemi di 3 numeri interi (chiamiamoli a, b e c) che soddisfano il teorema di Pitagora— a² + b² = c². Ovvero, possono formare un triangolo rettangolo con lati di lunghezza a, b e c. La quantità di numeri che soddisfano questa relazione è limitata, ma i matematici si divertono a cercarne di nuovi.

A parte il fattore curiosità di questa relazione, ha alcune interessanti proprietà che vengono sfruttate nella crittografia. Date le applicazioni che si possono trovare per questi insiemi di numeri, i matematici hanno esplorato anche oltre, utilizzando 4, 5 e altri insiemi di numeri che soddisfano una relazione simile in cui la somma dei quadrati di tutti i numeri tranne uno, dà il quadrato del numero rimasto.

Molto legato a queste terne pitagoriche è anche il famigerato ultimo teorema di Fermat in cui il quasi leggendario matematico criptico Pierre Fermat affermò che non poteva esistere un insieme di tre numeri interi che soddisfacessero la relazione — aⁿ + bⁿ = cⁿ per n maggiori di 2. Questa congettura è stata dimostrata solo nel 1995, più di 300 anni dopo la sua prima formulazione, ed è considerata uno dei più importanti problemi matematici del secolo.

Abbiamo parlato molto dei triangoli, in particolare dei triangoli rettangoli, e delle loro applicazioni in matematica e geometria. Quello di cui non abbiamo ancora parlato è l'utilità dei triangoli rettangoli per il calcolo nella vita reale. Potrebbe sembrare che le applicazioni al di fuori della geometria siano limitate, ma diamo un'occhiata alle ombre.

Sì, le ombre. L'ombra scura proiettata da un oggetto quando è illuminato. Se osservassi la forma formata dall'ombra, dall'oggetto e dal terreno, noteresti che si tratta di un triangolo rettangolo! Almeno, lo è quando l'oggetto è perfettamente verticale e il terreno è orizzontale. Nella maggior parte dei casi è così, o almeno ci si avvicina. Questo significa che possiamo usare il calcolatore per il triangolo rettangolo per trovare diverse informazioni sugli oggetti sotto il sole. Vediamo come.

Immagina di avere un edificio di cui vogliamo conoscere l'altezza, ma non puoi misurarlo direttamente perché è troppo alto per far cadere un metro dalla cima. Quello che puoi fare è misurare la lunghezza dell'ombra sulla strada. Poi, con l'aiuto di un qualsiasi strumento di misurazione angolare e di un foglio di carta, puoi trovare l'angolo tra l'ombra e il terreno. Sapendo che l'angolo tra l'edificio e il terreno è di 90°, puoi ottenere il valore dell'altezza dell'edificio.

Utilizzando questa tecnica, puoi misurare l'altezza di molti oggetti a patto che tu abbia a disposizione una luminosa giornata di sole o altre fonti di luce per illuminare l'oggetto. In effetti, questa era una tecnica di misurazione molto comune nei tempi passati. Probabilmente l'uso più interessante e strabiliante dei triangoli rettangoli è quello di Eratostene, che riuscì a utilizzare i triangoli rettangoli e le ombre per misurare il raggio della Terra.

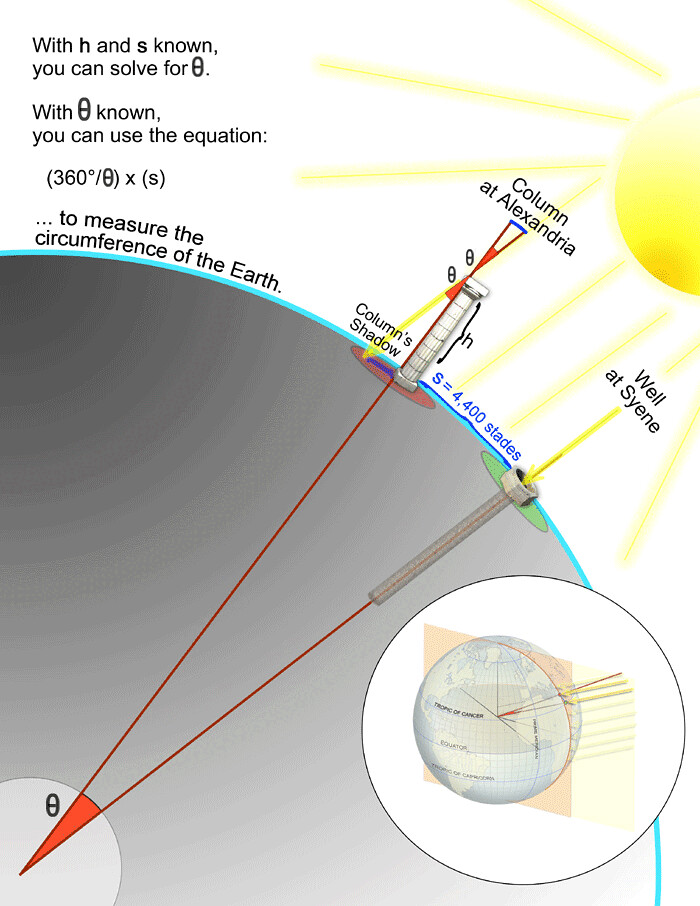
Eratostene notò che durante il solstizio d'estate c'era un luogo sulla Terra in cui i pozzi non avevano ombra a mezzogiorno, cioè il sole splendeva direttamente su di essi. Notando questo fatto, installò una colonna di altezza nota a una distanza nota da quel pozzo e misurò le dimensioni dell'ombra creata dal palo a mezzogiorno del giorno del solstizio. Quindi, utilizzando i triangoli rettangoli e la trigonometria, fu in grado di determinare l'angolo che passa dal centro della Terra tra il pozzo e il polo, nonché il raggio della Terra, in base alla distanza nota tra questi due punti.

Si trattava di un'impresa davvero sorprendente che ora puoi fare in modo molto più facile, semplicemente utilizzando i calcolatori di Omni che abbiamo creato per te.