Calcolatore per l'Area del Triangolo Rettangolo

Q: Qual è l'area di un triangolo rettangolo con ipotenusa di 5 cm e angolo di 45°?

L'area è 6,25 cm 2 . Otteniamo questa risposta applicando la formula area = c² × sin(α) × cos(α) / 2 con c = 5 e α = 45° . Il teorema matematico utilizzato per ricavare questa formula è chiamato legge dei seni .

Q: Come si chiamano i lati del triangolo rettangolo?

I due lati perpendicolari tra loro sono chiamati cateti . Il lato opposto all'angolo retto (in altre parole, il lato più lungo) è l' ipotenusa .

Creatori

Dott. Hanna Pamuła, Ph.D.

Hanna Pamuła

PhD

Website

Research Gate

Hanna (Hania) Pamuła holds a Ph.D. in Bioacoustics / Mechanical Engineering, obtained at AGH University of Science and Technology. She has participated in research work in labs in France and the UK and presented papers at several international conferences. Hania has a penchant for photography and graphic design. When not in the office, she’s probably traveling, hiking, or out in the field, watching birds and recording their calls. See full profile

Check our editorial policy

Traduttori

Rangsimatiti Binda Saichompoo

Environmental matters and supporting sustainability are always the most important aspects of Kat’s goals. Hence, Kat directed her education towards biomaterials, sustainability, and bioeconomy. Despite this major path, psychology, language, and culture are also her other strong fields of interest! Thanks to her Erasmus Joint Master’s degree, learning and adapting to new cultures is a piece of cake. See full profile

Check our editorial policy

e Sara Naouar

Sara Naouar

Sara is a dedicated student pursuing a Bachelor’s degree in Interpreting and Translation at Iulm University, Milan. She’s interested in the development of literature and the transformation of linguistics influenced by the cyber economy. She has a never-ending list of new places to travel to and explore. See full profile

Check our editorial policy

Revisori

Bogna Szyk

Nuovo

Se ti stai chiedendo come trovare l'area del triangolo rettangolo, sei nel posto giusto — questo calcolatore per l'area del triangolo rettangolo è lo strumento che fa per te.

Che tu stia cercando l'equazione dei cateti, dell'ipotenusa, o del lato e dell'angolo del triangolo rettangolo, questo calcolatore non ti deluderà.

Scorri in basso per saperne di più sulle formule dell'area del triangolo rettangolo o prova semplicemente il nostro calcolatore!

Formule per l'area del triangolo rettangolo

🙋 Se hai appena notato che il tuo triangolo non è un triangolo rettangolo, dai un'occhiata a questo calcolatore per l'area del triangolo.

L'equazione di base è una versione trasformata della formula standard dell'altezza del triangolo ( $a \cdot h / 2$ ). Poiché i cateti del triangolo rettangolo sono perpendicolari tra loro, un cateto viene considerato come base e l'altro come altezza del triangolo rettangolo:

\text{Area}=\frac{a\cdot b}{2}

A volte non è così ovvio — potresti avere altri valori che, nello specifico, non sono i due cateti. E allora?

Se sono dati un cateto e l'ipotenusa, usa il teorema di Pitagora per trovare il cateto mancante:

\qquad a^2+b^2=c^2

Quindi calcola la radice quadrata dell'equazione trasformata:

Dati $a$ e $c$ troviamo che $b = \sqrt{c^2 - a^2}$ :

\qquad\text{Area}=a\cdot\frac{\sqrt{c^2-a^2}}{2}

Dati $b$ e $c$ calcoliamo che $a = \sqrt{c^2 - b^2}$ :

\qquad \text{Area} = b\cdot\frac{\sqrt{c^2-b^2}}{2}

Se conosci un angolo e l'ipotenusa, puoi usare la legge dei seni su questo triangolo:

\qquad a=c\cdot\sin(\alpha)

Quindi:

\qquad \begin{split} b&=c\cdot\sin(\beta)\\&=c\cdot\sin(90\degree-\alpha)\\ &=c\cdot\cos(\alpha) \end{split}

Così:

\qquad \text{Area}=c^2\cdot\sin(\alpha)\cdot\frac{\cos(\alpha)}{2}

Dati un angolo e un cateto, trova l'area utilizzando ad esempio le funzioni trigonometriche:

\qquad\frac{a}{b}=\tan(\alpha)

\qquad\frac{b}{a}=\tan(\beta)

Troviamo:

\qquad \begin{split} \text{Area}&=b\cdot\tan(\alpha)\cdot\frac{b}{2}\\ \\[1.5em] &=b^2\cdot\frac{\tan(\alpha)}{2} \end{split}

Oppure:

\qquad \begin{split} \text{Area}&=a\cdot a\cdot \frac{\tan(\beta)}{2}\\[1em] &=a^2\cdot\frac{\tan(\beta)}{2} \end{split}

🙋 Vuoi saperne di più sui triangoli rettangoli? Visita il nostro calcolatore per il triangolo rettangolo!

Area del triangolo isoscele rettangolo

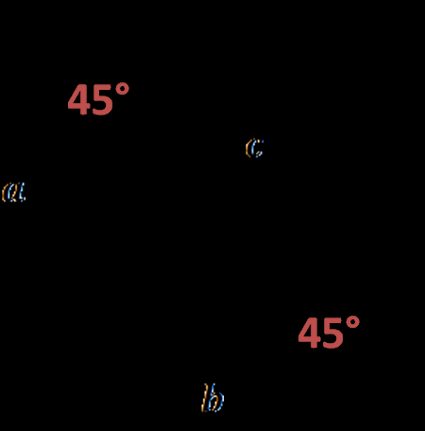
Il triangolo isoscele rettangolo è un triangolo rettangolo speciale, a volte chiamato triangolo 45 45 90 (è così speciale che abbiamo creato uno strumento apposito, il triangolo 45 45 90). In un triangolo di questo tipo, i due cateti sono di lunghezza uguale (poiché l'ipotenusa deve sempre essere il più lungo dei lati del triangolo rettangolo):

a=b

Un cateto è la base e l'altro è l'altezza — tra loro c'è un angolo retto. Quindi l'area del triangolo rettangolo isoscele è:

\text{Area}=\frac{a^2}{2}

Come si usa il calcolatore per l'area del triangolo rettangolo?

Mostriamo il calcolo passo dopo passo:

Scegli un'opzione, in base a ciò che hai indicato. Supponiamo di conoscere un cateto e un angolo, quindi cambiamo la selezione in dato un angolo e un cateto;
Inserisci i valori. Ad esempio, sappiamo che $\alpha = 40\degree$ e $b$ sono $17\ \text{cm}$ ; e
Guarda il nostro calcolatore per l'area del triangolo rettangolo che esegue tutti i calcoli per te! L'area del triangolo scelto è $121,\!25\ \text{cm}^2$ .

FAQ

Come si trova l'area di un triangolo rettangolo dati i lati?

Il metodo dipende dai lati che ti vengono forniti:

Se conosci le due gambe, usa la formula area = a × b / 2, dove a e b sono i lati; e
Se conosci un cateto "a" e l' ipotenusa "c", usa la formula: Area = a × √(c² - a²) / 2.

Qual è l'area di un triangolo rettangolo con ipotenusa di 5 cm e angolo di 45°?

L'area è 6,25 cm². Otteniamo questa risposta applicando la formula area = c² × sin(α) × cos(α) / 2 con c = 5 e α = 45°. Il teorema matematico utilizzato per ricavare questa formula è chiamato legge dei seni.

Come faccio a sapere se è un triangolo rettangolo?

Se ti vengono dati tre lati di un triangolo e vuoi sapere se questo triangolo è rettangolo, controlla se la teorema di pitagora è valida: a² + b² = c², dove c è il lato più lungo e a e b sono gli altri due lati.

Come si chiamano i lati del triangolo rettangolo?

I due lati perpendicolari tra loro sono chiamati cateti. Il lato opposto all'angolo retto (in altre parole, il lato più lungo) è l'ipotenusa.