Calcolatore di Radice Quadrata

Il nostro calcolatore di radice quadrata stima la radice quadrata di qualsiasi numero positivo che desideri. Basta inserire il numero scelto e leggere i risultati. Tutto viene calcolato velocemente e automaticamente! Con questo strumento puoi anche stimare il quadrato del numero desiderato (basta inserire il valore nel secondo campo), il che può essere di grande aiuto per trovare quadrati perfetti dalla formula della radice quadrata.

Sei alle prese con le operazioni aritmetiche di base: aggiungere radici quadrate, sottrarre radici quadrate, moltiplicare radici quadrate o dividere radici quadrate? Non è un problema! Nel seguente testo troverai una spiegazione dettagliata delle diverse proprietà delle radici quadrate, ad esempio come elevare le radici quadrate, con molti esempi. Con questo articolo imparerai una volta per tutte a trovare le radici quadrate!

Ti è mai passata in mente quale sia l'origine del simbolo della radice quadrata √? Ti assicuriamo che questa storia non è così semplice come potresti pensare all'inizio. L'origine del simbolo della radice risale all'antichità, come l'origine della percentuale.

Se stai cercando il grafico della radice quadrata o le proprietà della funzione della radice quadrata, vai direttamente alla sezione appropriata (basta cliccare sui link qui sopra!). Lì ti spieghiamo cos'è la derivata di una radice quadrata utilizzando una definizione fondamentale di radice quadrata; inoltre, ti spieghiamo come calcolare le radici quadrate degli esponenti o le radici quadrate delle frazioni. Infine, se sei abbastanza persistente, scoprirai che è possibile calcolare la radice quadrata di un numero negativo. In questo modo, introduciamo i numeri complessi che trovano ampie applicazioni in fisica e matematica.

L'operazione della radice quadrata di un numero era già nota nell'antichità. La prima tavoletta di argilla con il valore corretto fino a 5 decimali di √2 = 1,41421 proviene dalla Babilonia (1800 a.C. - 1600 a.C.). Molti altri documenti dimostrano che le radici quadrate erano utilizzate anche dagli antichi Egizi, Indiani, Greci e Cinesi. Tuttavia, l'origine del simbolo della radice √ è ancora largamente speculativa.

• Molti studiosi ritengono che le radici quadrate abbiano origine dalla lettera "r", la prima lettera della parola latina radix che significa radice; e
• Un'altra teoria sostiene che il simbolo della radice quadrata sia stato preso dalla lettera araba ج che è stata inserita nella sua forma originale di ﺟ nella parola جذر — radice (la lingua araba è scritta da destra a sinistra).

Il primo utilizzo del simbolo della radice quadrata √ non includeva la "barra" orizzontale sopra i numeri all'interno del simbolo della radice quadrata (o simbolo radicale), √‾. La "barra" è nota in latino come vinculum, che significa legame. Sebbene il simbolo radicale con il vinculum sia ormai di uso comune, di solito si omette questa sottolineatura in molti testi, come ad esempio negli articoli su internet. La notazione dei gradi superiori di una radice è stata suggerita da Albert Girard, che ha inserito l'indice di grado all'interno dell'apertura del segno radicale, ad esempio ³√ o ⁴√.

L'ultima domanda è: perché l'operazione di radice quadrata viene chiamata radice, indipendentemente dalla sua vera origine? La spiegazione diventa più evidente se scriviamo l'equazione x = ⁿ√a in una forma diversa: xⁿ = a. L'x è chiamata radice o radicale perché è la base nascosta di a. Quindi, la parola radicale non significa di grande portata o estrema, ma piuttosto fondamentale, che raggiunge la causa principale.

In matematica, le operazioni tradizionali sui numeri sono l'addizione, la sottrazione, la moltiplicazione e la divisione. Tuttavia, a volte aggiungiamo a questo elenco alcune operazioni e manipolazioni più avanzate: radici quadrate, esponenti, logaritmi e persino funzioni trigonometriche (ad esempio, seno e coseno). In questo articolo ci concentreremo solo sulla definizione di radice quadrata.

La radice quadrata di un dato numero x è ogni numero y il cui quadrato y² = y × y produce il numero originale x. Pertanto, la formula della radice quadrata può essere espressa come:

√x = y ⟺ x = y²,

dove ⟺ è un simbolo matematico che significa se e solo se. Ogni numero reale positivo ha sempre due radici quadrate — la prima è positiva e la seconda è negativa. Tuttavia, per molti scopi pratici, di solito utilizziamo quella positiva. L'unico numero che ha una sola radice quadrata è lo zero. Questo perché √0 = 0 e lo zero non è né positivo né negativo.

Esiste anche un'altra notazione comune delle radici quadrate che potrebbe essere più comoda in molti calcoli complessi. Questa formula alternativa della radice quadrata afferma che la radice quadrata di un numero è un numero elevato all'esponente ¹/₂:

√x = x^(1/2) = x^0,5

Nell'interpretazione geometrica, la radice quadrata di una data area di un quadrato dà la lunghezza del suo lato. Ecco perché √ ha la parola quadrato nel suo nome. Una situazione simile si verifica con la radice cubica, ∛. Se si prende la radice cubica del volume di un cubo, si ottiene la lunghezza dei suoi spigoli. Mentre le radici quadrate vengono utilizzate per considerare le aree superficiali, le radici cubiche sono utili per determinare quantità che si riferiscono al volume, ad esempio la densità.

Forse non siamo molto modesti, ma pensiamo che la risposta migliore alla domanda "Come calcolare la radice quadrata?" sia semplice: usando il calcolatore di radice quadrata! Puoi usarlo sia sul tuo computer che sul tuo smartphone per stimare rapidamente la radice quadrata di un dato numero. Purtroppo, a volte ci sono situazioni in cui hai a disposizione solo il tuo cervello. E allora? Per prepararti a questa evenienza, devi ricordare alcune nozioni di base sulle radici quadrate perfette:

• Radice quadrata di 1: √1 = 1, dato che 1 × 1 = 1;

• Radice quadrata di 4: √4 = 2, dato che 2 × 2 = 4;

• Radice quadrata di 9: √9 = 3, dato che 3 × 3 = 9;

• Radice quadrata di 16: √16 = 4, dato che 4 × 4 = 16;

• Radice quadrata di 25: √25 = 5, dato che 5 × 5 = 25;

• Radice quadrata di 36: √36 = 6, dato che 6 × 6 = 36;

• Radice quadrata di 49: √49 = 7, dato che 7 × 7 = 49;

• Radice quadrata di 64: √64 = 8, dato che 8 × 8 = 64;

• Radice quadrata di 81: √81 = 9, dato che 9 × 9 = 81;

• Radice quadrata di 100: √100 = 10, dato che 10 × 10 = 100;

• Radice quadrata di 121: √121 = 11, dato che 11 × 11 = 121; e

• Radice quadrata di 144: √144 = 12, dato che 12 × 12 = 144.

I numeri sopra riportati sono le radici quadrate più semplici perché ogni volta si ottiene un numero intero. Cerca di ricordarli! Ma cosa puoi fare quando c'è un numero che non ha una radice quadrata così semplice? Ci sono diverse soluzioni. Innanzitutto, puoi provare a prevedere il risultato per tentativi. Supponiamo che tu voglia stimare la radice quadrata di 52:

1. Sai che √49 = 7 e √64 = 8, quindi √52 dovrebbe essere compreso tra 7 e 8;

2. Il numero 52 è più vicino al 49 (di fatto più vicino al 7), quindi puoi provare a indovinare che √52 è 7,3;

3. Quindi, eleva al quadrato 7,3, ottenendo 7,3² = 53,29 (come dice la formula della radice quadrata), che è superiore a 52. Devi provare con un numero più piccolo, ad esempio 7,2; e

4. Il quadrato di 7,2 è 51,84. Ora hai un numero più piccolo, ma molto più vicino a 52. Se questa precisione ti soddisfa, puoi terminare le stime qui. Altrimenti, puoi ripetere la procedura con un numero scelto tra 7,2 e 7,3, ad esempio 7,22, e così via.

Un altro approccio consiste nel semplificare prima la radice quadrata e poi utilizzare le approssimazioni delle radici quadrate dei numeri primi (tipicamente arrotondate a due cifre decimali):

• Radice quadrata di 2: √2 ≈ 1,41;
• Radice quadrata di 3: √3 ≈ 1,73;
• Radice quadrata di 5: √5 ≈ 2,24;
• Radice quadrata di 7: √7 ≈ 2,65;
• Radice quadrata di 11: √11 ≈ 3,32;
• Radice quadrata di 13: √13 ≈ 3,61;
• Radice quadrata di 17: √17 ≈ 4,12;
• Radice quadrata di 19: √19 ≈ 4,34; ecc.

Proviamo di nuovo a trovare la radice quadrata di 52. Puoi semplificarla in √52 = 2√13 (imparerai a semplificare la radice quadrata nella prossima sezione) e poi sostituire √13 ≈ 3,61. Infine, fai una moltiplicazione √52 ≈ 2 × 3,61 = 7,22. Il risultato è lo stesso di prima!

In alcune situazioni non è necessario conoscere il risultato esatto della radice quadrata. In questo caso, il nostro calcolatore di radice quadrata è l'opzione migliore per stimare il valore di ogni radice quadrata che desideri. Ad esempio, supponiamo che tu voglia sapere se 4√5 è maggiore di 9. Dal calcolatore, sai che √5 ≈ 2,23607, quindi 4√5 ≈ 4 × 2,23607 = 8,94428. È molto vicino al 9, ma non è maggiore di esso! Il calcolatore di radice quadrata fornisce il valore finale con una precisione relativamente alta (a cinque cifre nell'esempio precedente).

Ricorda che il nostro calcolatore ricalcola automaticamente i numeri inseriti in uno dei campi. Puoi trovare la radice quadrata di un numero specifico riempiendo il primo campo oppure elevare al quadrato un numero che hai inserito nella seconda finestra. La seconda opzione è utile per trovare i quadrati perfetti che sono essenziali in molti aspetti della matematica e della scienza. Ad esempio, se inserisci 17 nel secondo campo, scoprirai che 289 è un quadrato perfetto.

In alcune applicazioni della radice quadrata, in particolare quelle relative a scienze come la chimica e la fisica, i risultati sono preferibili in notazione scientifica. In breve, una risposta in notazione scientifica deve avere un punto decimale tra i primi due numeri non nulli. Sarà rappresentata come il decimale moltiplicato per 10 elevato a esponente. Ad esempio, il numero 0,00345 si scrive come 3,45 × 10⁻³ in notazione scientifica, mentre 145,67 si scrive come 1,4567 × 10² in notazione scientifica. I risultati ottenuti con il calcolatore di radice quadrata possono essere convertiti in notazione scientifica con il calcolatore per la notazione scientifica.

Per prima cosa, chiediamoci quali radici quadrate possono essere semplificate. Per rispondere, devi prendere il numero che si trova dopo il simbolo della radice quadrata e trovare i suoi fattori. Se uno dei suoi fattori è un numero quadrato (4, 9, 16, 25, 36, 49, 64 e così via), allora puoi semplificare la radice quadrata. Perché questi numeri sono numeri quadrati? Possono essere espressi rispettivamente come 2², 3², 4², 5², 6², 7² e così via. Secondo la definizione di radice quadrata, si possono chiamare quadrati perfetti. Vediamo alcuni esempi:

• Si può semplificare √27? Con il calcolatore di cui sopra, si ottengono i fattori di 27: 1, 3, 9, 27. Qui c'è il 9! Questo significa che puoi semplificare √27; oppure

• Puoi semplificare √15? I fattori di 15 sono 1, 3, 5 e 15. Non ci sono quadrati perfetti in questi numeri, quindi questa radice quadrata non può essere semplificata.

Quindi, come semplificare le radici quadrate? Per spiegarlo, utilizzeremo una proprietà utile per la radice quadrata di cui abbiamo parlato in precedenza, ovvero la formula alternativa della radice quadrata:

√x = x^(1/2).

Possiamo utilizzare queste due forme di radice quadrata e passare da una all'altra ogni volta che vogliamo. Nello specifico, ricordiamo che la potenza del prodotto di due numeri specifici è equivalente al prodotto di quei numeri elevati a potenze uguali. Pertanto, possiamo scrivere:

(x × y)^(1/2) = x^(1/2) × y^(1/2) ⟺ √(x × y) = √x × √y,

Come puoi utilizzare queste conoscenze? Il radicando di una radice quadrata di solito non è un quadrato perfetto facilmente calcolabile, ma può contenere un quadrato perfetto tra i suoi fattori. In altre parole, puoi scriverlo come una moltiplicazione di due numeri, dove uno dei numeri è un quadrato perfetto, ad esempio 45 = 9 × 5 (9 è un quadrato perfetto). Il requisito di avere almeno un fattore che sia un quadrato perfetto è necessario per semplificare la radice quadrata. A questo punto, dovresti sapere quale sarà il prossimo passo. Devi mettere questa moltiplicazione sotto la radice quadrata. Nel nostro esempio:

√45 = 45^(1/2) = (9 × 5)^(1/2) = 9^(1/2) × 5^(1/2) = √9 × √5 = 3√5.

Hai semplificato con successo la tua prima radice quadrata! Naturalmente non è necessario scrivere tutti questi calcoli. Se ricordi che la radice quadrata è equivalente alla potenza ¹/₂, puoi abbreviarli. Esercitiamoci a semplificare le radici quadrate con altri esempi:

• Come semplificare la radice quadrata di 27?

  √27 = √(9 × 3) = √9 × √3 = 3√3;

• Come semplificare la radice quadrata di 8?

  √8 = √(4 × 2) = √4 × √2 = 2√2; e

• Come semplificare la radice quadrata di 144?

  √144 = √(4 × 36) = √4 × √36 = 2 × 6 = 12.

Nell'ultimo esempio, non è stato necessario semplificare la radice quadrata perché 144 è un quadrato perfetto. Puoi semplicemente ricordare che 12 × 12 = 144. Tuttavia, volevamo mostrarti che con il processo di semplificazione puoi calcolare facilmente anche le radici quadrate dei quadrati perfetti. È utile quando si ha a che fare con numeri grandi.

Infine, potresti chiederti come semplificare le radici di ordine superiore, ad esempio radici cubiche. In realtà il processo è molto simile a quello delle radici quadrate, ma nel caso delle radici cubiche devi trovare almeno un fattore che sia un cubo perfetto, non un quadrato perfetto, cioè 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ e così via. Quindi, dividi il numero in due parti e mettile sotto la radice cubica. Facciamo il seguente esempio di semplificazione di ³√192:

∛192 = ∛(64 × 3) = ∛64 × ∛3 = 4∛3.

A prima vista può sembrare un po' complicato, ma dopo un po' di pratica, sarai in grado di semplificare le radici a mente. Fidati di noi!

Addizione di radici quadrate e sottrazione di radici quadrate

Purtroppo, addizionare o sottrarre radici quadrate non è facile come addizionare o sottrarre numeri normali. Ad esempio, se 2 + 3 = 5, non significa che √2 + √3 sia uguale a √5. È sbagliato! Per capire perché, immagina di avere due tipi di forme diverse: triangoli 🔺 e cerchi 🔵. Cosa succede quando metti insieme un triangolo a un cerchio 🔺 + 🔵? Niente! Hai ancora un triangolo e un cerchio 🔺 + 🔵. D'altra parte, cosa succede quando provi a mettere insieme tre triangoli e cinque triangoli: 3🔺 + 5🔺? Ti ritroverai con otto triangoli 8🔺.

L'addizione di radici quadrate è molto simile a questa metafora. Il risultato dell'addizione di √2 + √3 è sempre √2 + √3. Non è possibile semplificare ulteriormente. La situazione è diversa, invece, quando entrambe le radici quadrate hanno lo stesso numero sotto il simbolo della radice. In questo caso possiamo sommarle come se fossero numeri (o triangoli) normali. Ad esempio, 3√2 + 5√2 è uguale a 8√2. Lo stesso vale per la sottrazione di radice quadrata. Vediamo altri esempi che illustrano questa proprietà della radice quadrata:

• Quanto fa 6√17 + 5√17? Risposta: 6√17 + 5√17 = 11√17;

• Quanto fa 4√7 - 7√7? Risposta: 4√7 - 7√7 = -3√7;

• Quanto fa 2√2 + 3√8? Risposta: 2√2 + 3√8 = 2√2 + 6√2 = 8√2, perché abbiamo semplificato √8 = √(4 × 2) = √4 × √2 = 2√2;

• Quanto fa √45 - √20? Risposta: √45 - √20 = 3√5 - 2√5 = √5, perché abbiamo semplificato √45 = √(9 × 5) = √9 × √5 = 3√5 e √20 = √(4 × 5) = √4 × √5 = 2√5;

• Quanto fa 7√13 + 2√22? Risposta: 7√13 + 2√22, non possiamo semplificare ulteriormente; e

• Quanto fa √3 - √18? Risposta: √3 - √18 = √3 - 3√2, non possiamo semplificare ulteriormente, ma abbiamo almeno semplificato √18 = √(9 × 2) = √9 × √2 = 3√2.

Moltiplicazione di radici quadrate e divisione di radici quadrate

Ora che l'addizione di radici quadrate è un gioco da ragazzi, facciamo un ulteriore passo avanti. Che ne dici di moltiplicare le radici quadrate e dividere le radici quadrate? Non ti spaventare! In realtà l'hai già fatto durante la lezione sulla semplificazione delle radici quadrate. La moltiplicazione delle radici quadrate si basa sulla proprietà della radice quadrata che abbiamo già usato qualche volta:

√x = x^(1/2)

Ti ricordi come si moltiplicano i numeri elevati alla stessa potenza? Come promemoria:

xⁿ × yⁿ = (x × y)ⁿ,

e quindi

x^(1/2) × y^(1/2) = (x × y)^(1/2) ⟺ √x × √y = √(x × y).

A differenza dell'addizione, puoi moltiplicare ogni radice quadrata. Ricorda che la moltiplicazione ha proprietà commutative, il che significa che l'ordine in cui due numeri vengono moltiplicati non ha importanza. Alcuni esempi chiariranno la questione:

• Quanto fa √3 × √2? Risposta: √3 × √2 = √6;

• Quanto fa 2√5 × 5√3? Risposta: 2√5 × 5√3 = 2 × 5 × √5 × √3 = 10√15, perché la moltiplicazione è commutativa;

• Quanto fa 2√6 × 3√3? Risposta: 2√6 × 3√3 = 2 × 3 × √6 × √3 = 6√18 = 18√2, abbiamo semplificato √18 = √(9 × 2) = √9 × √2 = 3√2.

La divisione di una radice quadrata è quasi la stessa cosa poiché:

x^(1/2) / y^(1/2) = (x / y)^(1/2) ⟺ √x / √y = √(x / y).

Tutto ciò che devi fare è sostituire il segno di moltiplicazione con una divisione. Tuttavia, la divisione non è un operatore commutativo! Devi calcolare separatamente i numeri che precedono le radici quadrate e i numeri sotto le radici quadrate. Come sempre, ecco alcuni esempi pratici:

• Quanto fa √15 / √3? Risposta: √15 / √3 = √5;

• Quanto fa 10√6 / 5√2? Risposta: 10√6 / 5√2 = (10 / 5) × (√6 / √2) = 2√3;

• Quanto fa 6√2 / 3√5? Risposta: 6√2 / 3√5 = (6 / 3) × (√2 / √5) = 2√(2/5) = 2√(0,4), siamo passati da una frazione semplice 2/5 alla frazione decimale 2/5 = 4/10 = 0,4.

Calcolare la radice quadrata di un numero elevato a una potenza o di una frazione potrebbe non esserti chiaro. Ma con le conoscenze che hai acquisito nella sezione precedente, dovrebbe essere più facile del previsto! Cominciamo con le radici quadrate di numeri elevati a una potenza n. In questo caso, sarà più facile per te utilizzare la forma alternativa di radice quadrata √x = x^(1/2). Ricordi la regola della potenza? In caso contrario, ecco un rapido promemoria:

(xⁿ)^m = x^{(n × m)},

dove n e m sono numeri reali qualsiasi. Ora, se metti 1/2 al posto di m, otterrai nient'altro che una frazione:

√(xⁿ) = (xⁿ)^(1/2) = x^(n/2),

ed ecco come trovare la radice quadrata di un numero elevato a una potenza. A proposito di potenze, l'equazione precedente è molto simile alla funzione di densità della distribuzione normale, molto utilizzata in statistica.

Se hai ancora dubbi su come calcolare la radice quadrata di numeri elevati a una potenza, ecco alcuni esempi:

• Radice quadrata di 2⁴:

  √(2⁴) = (2⁴)^(1/2) = 2^(4/2) = 2² = 4;

• Radice quadrata di 5³:

  √(5³) = (5³)^(1/2) = 5^(3/2); e

• Radice quadrata di 4⁵:

  √(4⁵) = (4⁵)^(1/2) = 4^(5/2) = (2²)^(5/2) = 2⁵ = 32.

Come puoi vedere, a volte è impossibile ottenere un bel risultato come nel primo esempio. Tuttavia, nel terzo esempio ti abbiamo mostrato un piccolo trucco per esprimere 4 come 2². Questo approccio può spesso semplificare le equazioni più complicate.

E le radici quadrate delle frazioni? Dai un'occhiata alla sezione precedente in cui abbiamo descritto come funziona la divisione di una radice quadrata. Lì puoi trovare la seguente relazione che dovrebbe spiegare tutto:

(x / y)^(1/2) ⟺ √x / √y = √(x / y),

dove x / y è una frazione. Di seguito puoi trovare alcuni esempi di radice quadrata di una frazione:

• Radice quadrata di 4/9:

  √(4/9) = √4 / √9 = 2/3;

• Radice quadrata di 1/100:

  √(1/100) = √1 / √100 = 1/10; e

• Radice quadrata di 1/5:

  √(1/5) = √1 / √5 = 1/√5 = √5/5.

Lasciare le radici nel denominatore non è una buona abitudine. Ecco perché ce ne siamo liberati nell'ultimo esempio. Abbiamo semplicemente moltiplicato sia il numeratore che il denominatore per lo stesso numero (possiamo sempre farlo, dato che il numero per cui moltiplichiamo è uguale a 1), in questo caso per √5.

Per calcolare la radice quadrata di numeri elevati usando il calcolatore di radice quadrata di Omni, inserisci i numeri nel formato di x^n.

Le funzioni giocano un ruolo fondamentale non solo in matematica, ma anche in molte altre aree come la fisica, la statistica o la finanza. La funzione f(x) non è altro che una formula che dice come cambia il valore di f(x) con l'argomento x. Troverai alcune funzioni che puoi applicare nella vita reale. Sono di grande aiuto se vuoi sapere come calcolare l'interesse composto o stimare il valore futuro di una rendita.

Qui sotto trovi il grafico della radice quadrata, composto dalla metà di una parabola. Controllalo e prova a verificare, ad esempio, se la funzione della radice quadrata di x = 9 è 3 e di x = 16 è 4 (come dovrebbe essere).

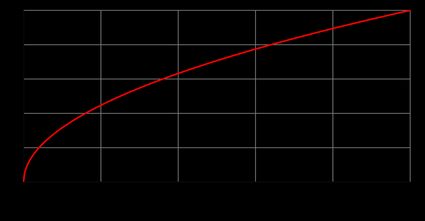
Torniamo alla funzione di radice quadrata f(x) = √x ed esploriamo le sue proprietà di base. Consideriamo solo la parte positiva di f(x) (come puoi vedere nel grafico della radice quadrata qui sopra). Quindi, la funzione radice quadrata:

• È continua e crescente per tutti gli x non negativi;

• È differenziabile per tutti gli x positivi (vedi la sezione "Funzione derivata di una radice quadrata" per maggiori informazioni);

• Si avvicina al limite dell'infinito quando x si avvicina all'infinito (lim √x → ∞ quando x → ∞); e

• È un numero reale per tutti gli x non negativi e un numero complesso per tutti gli x negativi.

La funzione derivata di un'altra funzione ci dice quanto velocemente questa funzione cambia con il suo argomento. Uno degli esempi più semplici in fisica è la posizione di un oggetto e la sua velocità (la velocità di variazione della posizione). Diciamo che la funzione x(t) descrive come cambia la distanza dell'auto in movimento da un punto specifico nel tempo t. Sai cosa determina la velocità di variazione della distanza percorsa? La risposta è la velocità dell'auto! Quindi la derivata della posizione x(t) è la velocità v(t) (anche la velocità può dipendere dal tempo). Per indicare la derivata, di solito si usa l'apostrofo v(t) = x'(t) o il simbolo della derivata v(t) = dx(t)/dt.

La derivata della funzione generale f(x) non è sempre facile da calcolare. Tuttavia, in alcune circostanze, se la funzione assume una forma specifica, abbiamo delle formule. Ad esempio, se

f(x) = xⁿ,

dove n è un numero reale qualsiasi, la funzione derivata è il seguente:

f'(x) = n × x^(n-1).

Potrebbe non sembrarlo, ma questo risponde alla domanda "Qual è la derivata di una radice quadrata?". Ricordi la forma alternativa (esponenziale) di una radice quadrata? Te la ricordiamo noi:

√x = x^(1/2).

Puoi notare che in questo caso n = 1/2, quindi la derivata di una radice quadrata è:

(√x)' = (x^(1/2))' = 1/2 × x^(-1/2) = 1/(2√x).

Poiché un numero n elevato a una potenza negativa equivale alla stessa potenza (questa volta positiva) di ¹/_n, la funzione derivata conterrà frazioni. Abbiamo uno strumento che potrebbe essere essenziale per sommare o sottrarre frazioni con denominatori diversi. Si chiama calcolatore di mcm e ti spiega come trovare il minimo comune multiplo.

La derivata di una radice quadrata è necessaria per ottenere i coefficienti della cosiddetta espansione di Taylor. Non vogliamo addentrarci troppo nei dettagli, quindi in breve la serie di Taylor ti permette di approssimare varie funzioni con i polinomi che sono molto più facili da calcolare. Ad esempio, l'espansione di Taylor di √(1 + x) intorno al punto x = 0 è data da:

√(1 + x) = 1 + 1/2 × x - 1/8 × x² + 1/16 × x³ - 5/128 × x⁴ + ...,

che è valida per -1 ≤ x ≤ 1. Sebbene l'espressione di cui sopra abbia un numero infinito di termini, per ottenere il valore approssimativo puoi utilizzare solo alcuni primi termini. Proviamo! Con x = 0,5 e i primi cinque termini, si ottiene:

√(1,5) = 1 + 1/2 × 0,5 - 1/8 × 0,25 + 1/16 × 0,125 - 5/128 × 0,0625,

√(1,5) ≈ 1,2241;

e il valore reale, fornito dal nostro calcolatore, è √(1,5) ≈ 1,2247. Abbastanza vicino!

Finora abbiamo fatto un sacco di calcoli ed equazioni. Per coloro che sono abbastanza ostinati, abbiamo preparato la prossima sezione che spiega come calcolare la radice quadrata di un numero negativo.

A scuola probabilmente ti hanno insegnato che la radice quadrata di un numero negativo non esiste. Questo è vero se si considerano solo i numeri reali. Molto tempo fa, per eseguire calcoli avanzati, i matematici hanno dovuto introdurre un insieme di numeri più generale — i numeri complessi. Possono essere espressi nella seguente forma:

x = a + b × i,

dove x è il numero complesso con la parte reale a e la parte immaginaria b. Ciò che differisce tra un numero complesso e uno reale è il numero immaginario i. Ecco alcuni esempi di numeri complessi: 2 + 3i, 5i, 1,5 + 4i e 2. Potrebbe sorprenderti di vedere 2, che è un numero reale. Sì, lo è, ma è anche un numero complesso con b = 0. I numeri complessi sono una generalizzazione dei numeri reali.

Finora, il numero immaginario i è probabilmente ancora un mistero per te. Che cos'è? Anche se può sembrare strano, è definito dalla seguente equazione:

i = √(-1),

ed è tutto ciò di cui hai bisogno per calcolare la radice quadrata di ogni numero, sia esso positivo o negativo. Vediamo alcuni esempi:

• Radice quadrata di -9: √(-9) = √(-1 × 9) = √(-1)√9 = 3i;
• Radice quadrata di -13: √(-13) = √(-1 × 13) = √(-1)√13 = i√13; e
• Radice quadrata di -49: √(-49) = √(-1 × 49) = √(-1)√49 = 7i.

Non è semplice? Questo problema non si pone con la radice cubica perché puoi ottenere il numero negativo moltiplicando tre numeri negativi identici (cosa che non puoi fare con due numeri negativi). Ad esempio:

³√(-64) = ³√[(-4)×(-4)×(-4)] = -4.

E questo è tutto ciò che devi sapere sulle radici quadrate!