Calcolatore per il Triangolo Isoscele

Il calcolatore per il triangolo isoscele è la scelta migliore se stai cercando una soluzione rapida ai tuoi problemi di geometria. Trova l'area del triangolo isoscele, il suo perimetro, il raggio del cerchio inscritto e circoscritto, le altezze e gli angoli, tutto in un unico posto. Se vuoi costruire una cuccia, scoprire l'area del frontone isoscele di un tempio greco o semplicemente fare i compiti di matematica, questo strumento è qui per te. Sperimenta il calcolatore o continua a leggere per saperne di più sulle formule del triangolo isoscele e sul teorema del triangolo isoscele.

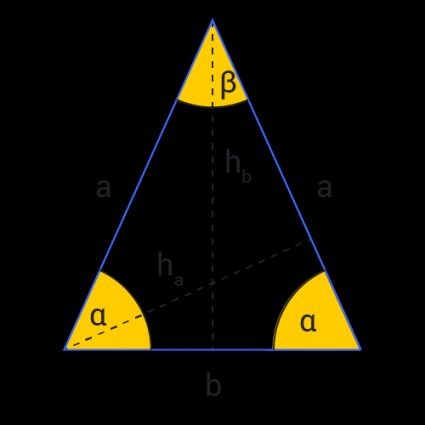
Un triangolo isoscele è un triangolo con due lati di uguale lunghezza, chiamati lati congruenti. Il terzo lato del triangolo è chiamato base. L'angolo di vertice è l'angolo tra i lati congruenti. Gli angoli che toccano la base sono chiamati angoli alla base.

Ecco le proprietà più importanti di un triangolo isoscele:

• Ha un'asse di simmetria lungo l'altezza del vertice;
• I due angoli opposti ai lati congruenti sono uguali; e
• Il triangolo isoscele può essere acutangolo, rettangolo o ottusangolo, ma dipende solo dall'angolo al vertice (gli angoli alla base sono sempre acuti).

Il triangolo equilatero è un caso speciale di triangolo isoscele. Puoi scoprire tutti i possibili tipi di triangoli nel calcolatore per la classificazione dei triangoli 🇺🇸. Inoltre, se vuoi approfondire le caratteristiche di un triangolo equilatero, consulta il calcolatore per il triangolo equilatero.

Per calcolare l'area del triangolo isoscele puoi utilizzare diverse formule. Le più popolari sono le equazioni:

1. Dati il lato congruente a e la base b:

   Area = (1/4) × b × √( 4 × a² - b² );

2. Data l'altezza h e la base b, o l'altezza da uno degli altri due vertici h2 e il lato congruente a:

   Area = 0,5 × h × b = 0,5 × h2 × a; e

3. Dato un angolo e un lato congruente o la base:

   Area = (1/2) × a × b × sin(angolo alla base) = (1/2) × a² × sin(angolo al vertice).

Inoltre, puoi consultare il nostro calcolatore per l'area del triangolo per trovare altre equazioni che funzionano per ogni tipo di triangolo, non solo per quello isoscele.

Per calcolare il perimetro del triangolo isoscele, basta sommare tutti i lati del triangolo:
Perimetro = a + a + b = 2 × a + b.

Il teorema del triangolo isoscele sostiene che se due lati di un triangolo sono congruenti, gli angoli opposti a questi lati sono congruenti.

Esiste anche il teorema inverso che afferma che se due angoli di un triangolo sono congruenti, allora i lati opposti a questi angoli sono congruenti.

Un triangolo aureo, chiamato anche triangolo sublime, è un triangolo isoscele in cui il lato congruente è in rapporto aureo con la base:

a / b = φ ~ 1,618

Il triangolo aureo ha alcune proprietà insolite:

• È l'unico triangolo con tre angoli in proporzione 2:2:1;
• È la forma dei triangoli che si trovano nei punti dei pentagrammi; e
• Si usa per formare una spirale logaritmica.

Scopriamo come utilizzare questo strumento con un semplice esempio. Dai un'occhiata a questa soluzione passo dopo passo:

1. Determina qual è il primo valore dato. Supponiamo di voler verificare le proprietà del triangolo d'oro. Digita 4,27 cm nel campo Lato congruente;
2. Inserisci il secondo parametro noto. Ad esempio, prendiamo una base pari a 2,54 cm;
3. Tutti gli altri parametri vengono calcolati in un batter d'occhio! Abbiamo verificato, ad esempio, che il perimetro del triangolo isoscele è di 11,08 cm e che gli angoli del triangolo aureo sono pari a 72° e 36° — il rapporto è infatti pari a 2:2:1.

Puoi usare questo calcolatore per determinare parametri diversi da quelli dell'esempio, ma ricorda che in genere esistono due triangoli isosceli distinti con una determinata area e altri parametri, ad esempio la lunghezza dei lati congruenti. Il nostro calcolatore mostrerà una possibile soluzione.