Calculadora de combinaciones y permutaciones

Esta calculadora de combinaciones y permutaciones (calculadora de combinaciones de n en k) es una herramienta que no solo te ayuda a encontrar el número de combinaciones de un conjunto (nCr), sino que también muestra todas las posibles combinaciones (o permutaciones) de cualquier conjunto de hasta 20 elementos. ¡Ten cuidado! Puede que el generador de combinaciones demore unos segundos en obtener todos los términos. Si te preguntas cuantas combinaciones diferentes pueden obtenerse a partir de un cierto número de elementos y un dado tamaño de muestra, ¡prueba nuestra calculadora de combinaciones!

Si todavía no te sientes seguro de lo que es una combinación, en el texto debajo lo explicaremos con más detalle. Allí encontrarás la definición de combinación junto con la fórmula de combinación (con y sin repeticiones). Te enseñaremos cómo calcular combinaciones, cómo se utilizan en probabilidad y lo que son las combinaciones lineales. Finalmente, discutiremos sobre la relación entre permutaciones y combinaciones. En forma breve, en las permutaciones importa el orden de los elementos, mientras que en combinaciones no. ¡Sigue leyendo para saber más!

¿Alguna vez te has preguntado cuáles son tus chances de ganar la lotería? ¿Qué tan probable es ganar el segundo premio? Para responder ambas cuestiones, debes recurrir a las combinaciones. Tenemos una herramienta dedicada específicamente a este problema. Nuestra calculadora de lotería 🇺🇸 no solo estima la probabilidad de ganar cualquier juego de lotería, sino que también te provee de una fórmula para ello. ¡Échale un vistazo! Pronto descubrirás que tan grandes (o pequeñas) son tus chances de ganar.

Según su definición, combinación se refiere al número de maneras en que puedes tomar r elementos de un conjunto de n elementos distintos (es por eso que a este tipo de problemas también se los denomina "n en r"). El orden en el que son escogidos los elementos no es de importancia, al contrario de las permutaciones (puedes hallar una explicación más extensiva en la sección permutación y combinación).

Hallar todas las combinaciones posibles de un conjunto de objetos es un problema puramente matemático. Probablemente, te hayan enseñado cómo hallar el máximo común divisor (MCD) o el mínimo común múltiplo (MCM). Calcular el número de combinaciones es algo completamente diferente. Veamos qué tan complicado puede resultar.

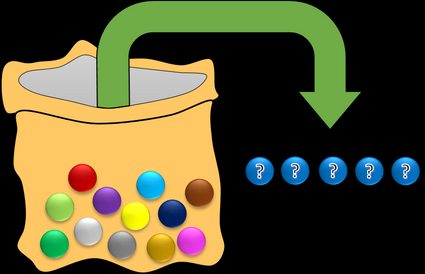
Imagina que hay 12 bolas dentro de una bolsa, cada una de un color distinto. Ahora escoges cinco aleatoriamente. ¿Cuántos conjuntos diferentes de bolas puedes obtener? O, en otras palabras, ¿cuántas combinaciones existen?

Los matemáticos nos brindan la solución exacta para distintos tipos de problemas, p. ej., cómo calcular el área o el volumen. ¿Existe un camino similar para obtener el número de combinaciones del ejemplo anterior?

Por suerte, ¡no necesitas escribir uno por uno todos los conjuntos posibles! ¿Cómo lo hago entonces? Puedes utilizar la siguiente fórmula de combinaciones que te permitirá determinar el número exacto sin perder tiempo:

donde:

• $C(n,r)$ es el número de combinaciones;
• $n$ es el número de elementos en el conjunto; y
• $r$ es el número de elementos que tomas a la vez del conjunto.

El signo de exclamación $!$ representa el factorial. Dirígete a nuestra calculadora factorial 🇺🇸 para aprender más. La expresión en el lado derecho es también denominada coeficiente binomial.

Apliquemos esta ecuación a nuestro problema de las bolas de colores. Debemos determinar cuántas combinaciones diferentes existen:

Puedes comparar el resultado con nuestra calculadora de combinaciones y permutaciones. ¡La calculadora también te dará un listado de todas las combinaciones posibles! Ten en cuenta, sin embargo, que 792 combinaciones de por sí son bastantes para mostrar. Para evitar una situación donde se generen demasiadas combinaciones, optamos por limitar el generador de combinaciones a un máximo de 2000 combinaciones, por defecto. Puedes modificar esto en el modo avanzado.

Puedes notar que, de acuerdo a la fórmula de combinaciones, el número de combinaciones al elegir de a un solo elemento a la vez es simplemente $n$. Por otro lado, si tomas todos los elementos del conjunto a la vez, solo existe una forma de hacerlo. Verifiquemos esta propiedad con nuestro ejemplo. El total de objetos es $n = 12$. Cada letra en la calculadora de combinaciones representa un color de bola distinto, p. ej., A es rojo, B es amarillo, C es verde, etcétera. Si solo tomas de a un elemento $r=1$ a la vez, el número de combinaciones posibles será $12$ - ya que hay 12 elementos distintos. Sin embargo, si tomas $r = 12$ elementos, solo habrá $1$ combinación que incluya a todas las bolas. ¡Utiliza nuestra calculadora de n en k y compruébalo!

A estas alturas, probablemente ya sepas todo lo que necesitas sobre combinaciones y la fórmula de combinaciones. Si requieres aprender un poco más, en las secciones siguientes escribimos más sobre combinaciones lineales, combinaciones en probabilidad y las diferencias entre permutación y combinación, usualmente (y erróneamente) confundidas entre sí.

Imagina la misma bolsa con bolas de distintos colores del ejemplo anterior. De nuevo, escoges cinco bolas al azar, pero esta vez, el orden sí importa - no será lo mismo tomar primero la bola roja que escogerla segunda. Veamos un ejemplo más claro donde escoges tres bolas denominadas R (roja), A (azul) y V (verde). Existen seis permutaciones de este conjunto (el orden de las letras determina el orden en que se escogen las bolas): RAV, RVA, ARV, AVR, VRA y VAR. ¡Pero la definición de combinación nos dice que solo hay una combinación! Esta es la diferencia fundamental.

Por definición, una permutación es una ordenación de todos los elementos de un conjunto en alguna secuencia u orden. Sin embargo, en los libros se suele generalizar este concepto y prescindir de utilizar todos los elementos del conjunto. Esto hace que las permutaciones y combinaciones sean similares. Según esta definición, una permutación determina el número de maneras en que puedes escoger y ordenar r elementos de un conjunto de n objetos diferentes. Esto se denomina r-permutaciones de n (también llamadas variaciones). Si buscas una explicación todavía más detallada, la calculadora de permutaciones 🇺🇸 puede ayudarte.

La fórmula de permutaciones se encuentra debajo:

¿Te resulta similar? Esta ecuación es parecida a la fórmula de combinaciones. De hecho, si sabes el número de combinaciones posible, puedes calcular el número de permutaciones con facilidad:

Si activas el modo avanzado de esta calculadora de combinaciones, podrás hallar el número de permutaciones.

Quizás te preguntes, ¿cuándo debo utilizar permutaciones en vez de combinaciones? Bueno, depende de si el orden importa o no. Por ejemplo, digamos que tienes un mazo de nueve cartas con los números del 1 al 9. Tomas tres cartas al azar y las alineas sobre la mesa, produciendo un número de tres dígitos, p. ej., 425 u 837. ¿Cuántos números diferentes puedes crear?

¡Revisa el resultado con nuestra calculadora! ¿Y cuántas combinaciones existen?

El número de combinaciones es siempre menor que el número de permutaciones. En este caso, es seis veces menor (si multiplicas 84 por $3! = 6$, obtendrás 504). Surge del hecho que cada trío de cartas puede ser ordenado en seis maneras diferentes, como en el ejemplo de las tres bolas de color.

Para completar esta diferenciación entre permutaciones y combinaciones, vamos a introducir un criterio similar, solo que esta vez permitiremos repeticiones. Esto significa que después de tomar un elemento de un conjunto de n objetos distintos, lo volveremos a colocar dentro del conjunto. En el ejemplo de las bolas de colores, tomas una bola de la bolsa, la memorizas y la devuelves a su lugar. Análogamente, en el ejemplo de las cartas, escoges una carta, escribes el número de la misma y la devuelves al mazo. De este modo, puedes obtener una combinación de dos bolas rojas o 228 como una permutación, por ejemplo.

Si crees que ambas fórmulas se vuelven más complicadas al permitir repeticiones, estás en lo correcto. Sin embargo, no es algo tan complejo como calcular el nivel de alcohol de una cerveza artesanal. De hecho, en el caso de las permutaciones, la ecuación se vuelve más simple. La fórmula para combinaciones con repetición es:

y para permutaciones con repetición:

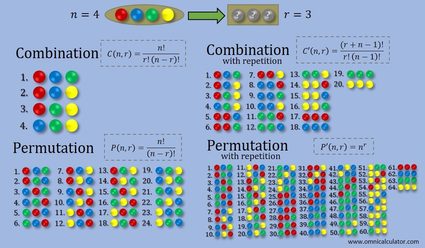
En la imagen debajo, se muestra un resumen de las diferencias entre los cuatro tipos de combinaciones y permutaciones: combinación, combinación con repetición, permutaciones, permutaciones con repetición. Se trata de un ejemplo en el que tienes cuatro bolas de distintos colores y tomas tres de ellas. En el caso de selecciones con repetición, puedes escoger la misma bola varias veces. Si quieres utilizar permutaciones en este ejemplo, ten cuidado, habrá miles de conjuntos distintos. De todos modos puedes calcular el número de permutaciones con nuestra calculadora usando el modo avanzado (advanced-mode).

Empecemos con combinaciones y probabilidad, algo que es de suma importancia en análisis estadísticos. El ejemplo anterior debería resultarnos útil para esto - escoges tres de cuatro bolas de colores de la bolsa. Supongamos que quieres saber cuáles son las chances (probabilidad) de que haya una bola roja entre ellas. Hay cuatro combinaciones diferentes y la bola roja se encuentra en tres de ellas. La probabilidad de esta combinación específica es, entonces:

Si tomaras tres bolas al azar, en el 75 % habría una bola roja en esta selección. Para expresar un resultado en probabilidad, se suele utilizar el símbolo de porcentaje.

Ahora, supongamos que escoges una bola, anotas el color en un papel y la devuelves a la bolsa. ¿Cuál es la probabilidad de que al menos una sea roja? Este es un problema de "combinaciones con repetición". Mirando la imagen de arriba, puedes ver que hay un total de veinte combinaciones diferentes y diez de ellas contienen a la bola roja, por lo tanto:

¿Esto te sorprende? No debería. Cuando devuelves la primera bola, p. ej., la azul, puedes volver a escogerla al azar en tu segundo y tercer intento. Las chances de que salga una bola roja, por lo tanto, disminuyen. ¿Cuál es la probabilidad de que la primera bola que tomes sea roja? Intenta resolverlo por tu cuenta.

Supongamos que desconfías de nuestros conocimientos o quieres verificarlo por ti mismo. Tomas tres bolas de cuatro y compruebas si hay una bola roja o no (como en el primer ejemplo de esta sección). Repites este proceso tres veces más y obtienes la bola roja solo en uno de los cuatro casos - $25\ \%$ de los casos. Basándote en lo dicho anteriormente, esperabas hallar la bola roja en el $75\ \%$ de los casos. ¿Qué ha sucedido? Nada en absoluto. ¡Así es como funciona la probabilidad! Existe una ley de los grandes números que describe el comportamiento de repetir un experimento un número muy grande de veces. Si repites el procedimiento de tomar tres bolas, p. ej., cien veces más, te acercarás poco a poco a $75\ \%$.

Es más, la ley de los grandes números casi siempre lleva hacia una distribución normal, que puede describir, por ejemplo, la inteligencia o altura de un conjunto de personas, a partir del valor p. ¿Quieres aprender más? ¡Dirígete a la calculadora de distribución normal 🇺🇸!

¿Has oído hablar de combinaciones lineales? A pesar de poseer la palabra combinación, no tienen mucho en común con los temas que hemos aprendido hasta aquí. Sin embargo, intentaremos explicarlo brevemente. Una combinación lineal es el resultado de tomar un conjunto de términos y multiplicar a cada uno de ellos por una constante y sumar los resultados. Esto se usa frecuentemente en física de ondas y física cuántica. Estos son algunos de los usos frecuentes de combinaciones lineales:

1. Vectores. Cada vector de tres dimensiones puede descomponerse en tres vectores unitarios $\^e_1 = (1,0,0)$, $\^e_2 = (0,1,0)$ y $\^e_3 = (0,0,1)$. Por ejemplo, $\vec{v} = (2,5,3) = 2\^e_1 + 5\^e_2 + 3\^e_3$ que es una combinación lineal.
2. Funciones. Digamos que tienes dos funciones $f(x) = \text{e}^x$ y $g(x) = \text{e}^{-x}$. A partir de ambas, puedes construir una combinación lineal que describe al seno hiperbólico $\sinh(x) = \frac{f(x)}{2} - \frac{g(x)}{2}$ o al coseno hiperbólico $\cosh(x) = \frac{f(x)}{2} + \frac{g(x)}{2}$. Puedes realizar algo similar para el seno y coseno, pero debes ayudarte con el número imaginario $i$. Encontrarás más sobre este tema en nuestra calculadora de raíz cuadrada 🇺🇸.
3. Polinomios. Por ejemplo, supongamos que tienes tres polinomios $p_1(x) = 1$, $p_2(x) = 3x + 3$, $p_3(x) = x^2 -x + 1$ y quieres expresar la función $q(x) = 2x^2 + x + 3$ como una combinación linear de dichos polinomios. No siempre es posible hacer esto, sin embargo, en este caso $q(x) = -2p_1(x) + p_2(x) + 2p_3(x)$.

En matemáticas, la diferencia fundamental entre combinaciones y permutaciones radica en si importa o no el orden de los objetos:

• En las permutaciones, el orden sí importa, por lo que ordenamos a los objetos de forma secuencial.
• En las combinaciones, el orden no importa, y escogemos un grupo de objetos a partir de un conjunto mayor.

Si ya tienes una combinación y quieres convertirla en una permutación, debes introducir un orden en el conjunto de objetos, i. e., escoger uno de los posibles ordenamientos para tu conjunto. Por lo tanto, el número de permutaciones de r objetos de una colección de n objetos totales es igual al número de combinaciones de r en n multiplicado por el número de posibles ordenamientos de estos r objetos, i. e., por r!.

Si ya tienes una permutación y quieres volverla una combinación, debes eliminar el ordenamiento de la misma, i. e., ignora todos los posibles ordenamientos del conjunto. Por lo tanto, el número de combinaciones de r objetos de una colección de n objetos totales es igual al número de permutaciones de r en n dividido por el número de ordenamientos posibles de estos r objetos, i. e., por r!.

Si las siete letras de la palabra son distintas, tienes 7! = 5040 maneras en las que puedes ordenarlas (el número de permutaciones de siete objetos). Sin embargo, si algunas letras se repiten, el número se reduce. Por ejemplo:

• Si la palabra fuera "TESTIGO", la letra "T" aparecerá dos veces, por lo que dividiríamos 7! por 2! = 2 dando como resultado 2520.
• Si la palabra fuera "RELEVAR", tendríamos "E" y "R" repetidas ambas dos veces, por lo que dividiríamos 7! por 2! × 2! = 4, resultando 1260.
• Si la palabra fuera "GALAXIA", la letra "A" aparece tres veces, entonces dividimos 7! por 3! = 6 y el resultado es 840.