Exponentielle Regression Rechner

Unser Exponentielle-Regression-Rechner ist immer dann für dich da, wenn du die Exponentialfunktion eines Datensatzes bestimmen musst, d. h. mit anderen Worten, um die Exponentielle Ausgleichskurve zu finden.

Was ist die exponentielle Regression? Lies weiter, denn wir geben dir nicht nur die Formel für die exponentielle Regression in die Hand, sondern erläutern, wie man die exponentielle Regression berechnet. Außerdem erklären wir dir, in welchen Situationen sich die exponentielle Anpassung als nützlich erweist. Als Bonus zeigen wir dir, wie du die Funktion der exponentiellen Regression herleiten kannst, damit du sie nicht auswendig lernen musst. 😉

Das Ziel der exponentiellen Regression ist es, eine Exponentialfunktion zu finden, die am besten zu einer gegebenen Menge von Datensätzen passt. Dies ist anderen Regressionsmodellen sehr ähnlich, die du mit den Omni-Tools entdecken kannst:

• Kleinste-Quadrate-Schätzung Rechner 🇺🇸, wo wir nach der passenden (geraden) Linie suchen;
• Quadratische Regression Rechner 🇺🇸, bei dem es um die Anpassung einer Parabel geht;
• Der Kubische Regression Rechner 🇺🇸 befasst sich mit kubischen Kurven (d. h. Kurven dritten Grades), und
• der Polynomiale Regression Rechner 🇺🇸, bei dem wir passendste Polynomkurve suchen.

Es gibt viele Situationen, in denen die Daten weder eine Gerade noch eine Parabel beschreiben, aber dich in Form einer Exponentialkurve darstellen lassen.; das sind Prozesse, die am Anfang langsam wachsen und sich dann schnell beschleunigen oder deren Zerfall schnell beginnt und sich dann mit der Zeit verlangsamt. Beispiele sind das Wachstum von Investitionen, die Temperatur von abkühlenden Objekten und der radioaktive Zerfall.

Nehmen wir an x sei die erklärende Variable und y die Antwortvariable. Dann lautet die exponentielle Regressionsgleichung y = a ∙ b^x, wobei a ≠ 0 und b > 0, b ≠ 1 ist. Die Koeffizienten a und b müssen so gewählt werden, dass die Gleichung der Exponentialkurve für den Datensatz am besten geeignet ist, (x₁, y₁), ..., (x_n, y_n) ;

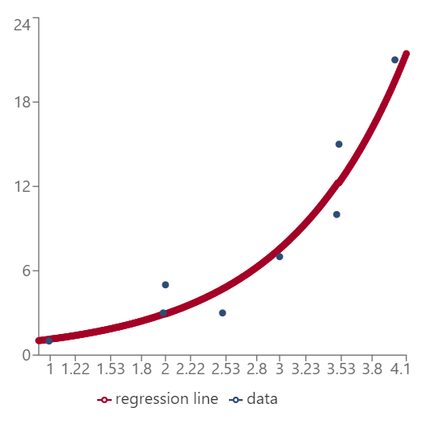
Im nächsten Abschnitt werden wir dir erklären, wie du die Koeffizienten a und b findest. Hier wollen wir ihre Bedeutung erläutern:

• a ist der Wert, der durch das exponentielle Regressionsmodell für x = 0 vorhergesagt wird;
• Wenn b > 1, beschreibt die exponentielle Anpassung ein exponentielles Wachstum; und
• Wenn 0 < b < 1, beschreibt die exponentielle Anpassung einen exponentiellen Zerfall.

Beachte, dass a ∙ b^x+1 = a ∙ b ∙ b^x vorliegt, d.h. wenn x um 1 Einheit steigt, wird y mit b multipliziert. Dies steht im starken Gegensatz zur linearen Regression y = m ∙ x + c, bei der eine Erhöhung von x um 1 Einheit dazu führt, dass der Wert von m (Steigung) zu y addiert wird!

Wir haben die Gleichung für die exponentielle Anpassung besprochen, aber wie berechnet man die exponentielle Regression, wenn man einige Daten gesammelt hat? Der Trick ist folgender:

1. Unsere Daten so umwandeln, dass sie ein lineares Modell zulassen.
2. Bestimme dieses lineare Modell, z. B. mit der Methode der kleinsten Quadrate.
3. Transformiere die Daten zusammen mit dem Modell zurück in die ursprüngliche Form.

Die Exponentielle Regression für die Daten (x, y) lautet:

y = exp(c) × exp(m × x),

wobei m die Steigung und c der Achsenabschnitt des linearen Regressionsmodells ist, das an die Daten (x, ln(y)) angepasst wurde. Im nächsten Abschnitt kannst du die Details der Herleitung sehen.

Mit dem exponentiellen Regressionsmodell versuchen wir, unsere Daten mithilfe der Gleichung in der Form y = a ∙ bˣ zu erklären. Hier zeigen wir dir, wie die Formel für die exponentielle Regression hergeleitet werden kann. Um die Koeffizienten a und b zu bestimmen, gehst du folgendermaßen vor:

1. Nimm den Logarithmus beider Seiten der Gleichung; wir haben die folgende äquivalente Gleichung:

   ln(y) = ln(a ∙ bˣ)

2. Die Eigenschaften von Logarithmen ergeben:

   ln(y) = ln(a) + ln(bˣ)

   und

   ln(y) = ln(a) + x ∙ ln(b)

3. Wir haben ln(y) als lineare Funktion von x ausgedrückt, mit der Steigung ln(b) und dem Achsenabschnitt ln(a).

4. Finde die beste Ausgeichsgerade für (x, ln(y)). Sagen wir, sie lautet ln(y) = c + x ∙ m.

5. Suche die a und b, die Folgendes erfüllen:

   ln(a) = c und ln(b) = m.

6. Um a und b zu berechnen, nimm den Exponenten (Antilogarithmus) der Steigung m und des Achsenabschnitts c:

   a = exp(c) und b = exp(m)

1. Gib deine Daten in den Rechner ein. Du kannst bis zu 30 Datenpunkte eingeben (neue Zeilen erscheinen, wenn du die Felder ausfüllst). Denke daran, dass wir mindestens 3 Punkte (beide Koordinaten!) brauchen, um ein Modell anzupassen.

2. Es erscheint ein Streudiagramm mit deinen Daten und der exponentielle Ausgleichskurve.

3. Unterhalb des Diagramms findest du die exponentielle Regressionsgleichung für deine Daten.

4. Falls nötig, kannst du in der Option Erweiterter Modus die Genauigkeit (Anzahl der signifikanten Stellen) erhöhen, mit der der Koeffizient berechnet wird. Die Standardpräzision ist auf 4 Ziffern eingestellt.

Die Formel für die Exponentialfunktion lautet f(x) = a ∙ b^x oder f(x) = ab^x, wobei a der Koeffizient, b die Basis und x der Exponent ist. Dies gilt, wenn a ≠ 0 und b > 0, b ≠ 1.

Um eine exponentielle Regression zu berechnen, musst du Folgendes tun:

1. Transformiere deine Daten so, dass sie ein lineares Modell zulassen.
2. Bestimme das spezifische lineare Modell mit der Methode der kleinsten Quadrate.
3. Transformiere die Daten und das Modell zurück in die ursprüngliche Form.

R² ist das Bestimmtheitsmaß bei der exponentiellen Regression. Mit anderen Worten: Der Wert von R² zeigt an, wie genau deine Regressionslinie deine Datenpunkte darstellt. Je näher R² bei 1 liegt, desto genauer ist die Regression.

Die Änderungsraten für y in Abhängigkeit von x sind unterschiedlich. Bei der linearen Regression ist die Veränderung von y eine konstante Addition, während bei der exponentiellen Regression die Veränderung von y eine konstante Multiplikation ist.

Zum Beispiel könnte der Wert von y bei der linearen Regression um +3 oder bei der exponentiellen Regression um ∙3 erhöhen, wie in der Tabelle dargestellt:

Benutze Desmos, um eine exponentielle Regression darzustellen:

1. Gib deine Datenpunkte (x₁ und y₁, etc.) ein, indem du sie in eine Tabelle einfügst oder sie aus Excel einfügst.
2. Deine Datenplots werden in deinem Desmos-Diagramm erscheinen.
3. Gib deine Exponentialgleichung oder dein Modell in die nächste Zelle ein, um eine exponentielle Regressionslinie in deinem Diagramm zu erstellen.
4. Du hast es geschafft!