Phasenverschiebung Rechner

Willkommen bei Omni's Phasenverschiebung-Rechner! Hier beschäftigen wir uns mit trigonometrischen Funktionen und der Berechnung ihrer Phasenverschiebung. Doch damit nicht genug: Wir erklären dir auch, wie man die Amplitude und die Periode bestimmt. Eine große Klasse von Funktionen verhält sich praktisch gleich und die Unterschiede beziehen sich nur auf die genaue Beschreibung der oben genannten Werte: die Amplitude, Periode und Phasenverschiebung. Zumindest bis zur vertikalen Verschiebung.

Wie wir bereits erwähnt haben, werden wir uns hier auf trigonometrische Funktionen konzentrieren: genauer gesagt auf den Sinus und Kosinus. Trotzdem ist es wichtig, daran zu denken, dass viele der Begriffe allgemeiner sind, besonders die horizontale Parallelverschiebung und vertikale Verschiebung.

Schauen wir uns zunächst ein Bild an, das die Amplitude, Periode, Phasenverschiebung und vertikale Verschiebung auf dem Graphen abbildet (das gleiche Bild erscheint oben im Rechner).

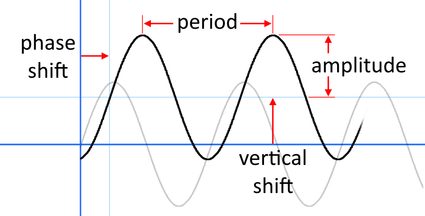
Wir können solche Funktionen mit der Formel für die Phasenverschiebung schreiben:

oder:

wobei $A$, $B$, $C$ und $D$ beliebige reelle Zahlen sind und $A$ und $B$ nicht Null sind (sonst wäre es keine trigonometrische Funktion). Offensichtlich bestimmen diese vier Zahlen die Amplitude, die Periode, die Phasenverschiebung und die vertikale Verschiebung. Das Bild zeigt in gewissem Maße, wie sie sich auf den Graphen auswirken. Dennoch wäre es sinnvoll, die Grafik mit einigen Definitionen zu unterstützen.

1. Die Amplitude gibt an, wie weit (in beiden Richtungen) die Werte von der waagerechten Ursprungsgerade des Diagramms entfernt sind. Für einfache Sinus- oder Kosinusfunktionen ist der Wert $1$, da die Mittelpunktlinie bei $0$ liegt, und die Werte der Funktionen von $-1$ bis $1$ reichen.

2. Die Periode ist die Länge auf der horizontalen Achse, nach der die Funktion beginnt, sich zu wiederholen. Mit anderen Worten: Der (unendliche) Graph ist nur eine Menge von aneinandergereihten, periodenlangen Kopien. Für eine einfache Sinus- oder Kosinusfunktion ist die Periode gleich $2\pi$, da $\sin(0) = \sin(2\pi) = \sin(4\pi) = ...$ und die Kurvenverläufe dazwischen genau gleich sind (ähnlich für den Kosinus).

3. Die Phasenverschiebung (auch Horizontalverschiebung genannt) beschreibt, wie weit der Graph vom normalen Sinus oder Kosinus horizontal verschoben wurde. Der Wert ist $0$, wenn wir die beiden Funktionen unverändert lassen.

4. Die vertikale Parallelverschiebung (auch vertikale Translation genannt) beschreibt, wie weit der Graph vertikal vom regulären Sinus oder Kosinus verschoben wurde. Der Wert ist gleich $0$, wenn die beiden Funktionen unverändert bleiben.

Jetzt haben wir gelernt, was die Phasenverschiebung ist und welche drei Werte sie hat. In den folgenden Abschnitten wird beschrieben, wie man jeden dieser Werte anhand der Formel für die Phasenverschiebung berechnet. Beginnen wir mit der Amplitude.

Das Konzept der Phasenverschiebung ist bei der Untersuchung von schwingenden und harmonischen Bewegungen weit verbreitet. Diese Phänomene sind also die besten Freunde der Trigonometrie. Du kannst die Verbindung in unserem Trigonometrie Rechner entdecken oder im Trigonometrische Funktionen Rechner 🇺🇸 mehr über die verschiedenen Funktionen eines Pendels erfahren. Du kannst natürlich auch direkt in den spezielleren Kosinus Rechner 🇺🇸 und Sinus Rechner 🇺🇸 schauen!

Wir wissen, dass die Sinus- und Kosinusfunktionen Werte zwischen $-1$ und $1$ haben. Diese einfache Tatsache ändert sich auch nicht, wenn wir $\sin(x)$ oder $\cos(x)$ durch $\sin(Bx - C)$ oder $\cos(Bx - C)$ durch $B$ und $C$ ersetzen, die nicht Null sind. Das liegt daran, dass die Funktion $f(x) = Bx - C$ dann eine Bijektion (d. h. eine Eins-zu-Eins-Entsprechung) auf den Raum der reellen Zahlen ist.

Schauen wir uns nun an, was passiert, wenn wir $D$ hinzufügen, d. h. wenn wir $\sin(Bx - C) + D$ oder $\cos(Bx - C) + D$ haben. Da der erste Teil etwas zwischen $-1$ und $1$ ergibt, wird das Ganze zwischen $-1 + D$ und $1 + D$ liegen (sieh zum Vergleich den Textabschnitt Wie man die vertikale Verschiebung findet). Das bedeutet, dass der Mittelwert auf $D$ fällt, und die Amplitude ist immer noch $1$, weil die Werte so weit wie $1$ von $D$ entfernt fallen.

Daher ist das Einzige, was die Amplitude in den Formeln für die Phasenverschiebung $A\cdot\sin(Bx - C) + D$ und $A\cdot\cos(Bx - C) + D$ beeinflussen kann, das Nicht-Null-$A$. Und in der Tat, da $\sin(Bx - C)$ und $\cos(Bx - C)$ die ganze Zeit zwischen $-1$ und $1$ liegen, ändert der Multiplikator $A$ diesen Bereich in $-1\cdot A = -A$ und $1 \cdot A = A$.

Ja, du hast es erraten: Die Amplitude der Phasenverschiebungs-Gleichungen $A \cdot\sin(Bx - C) + D$ und $A \cdot\cos(Bx - C) + D$ ist einfach gleich $A$.

Erinnere dich daran, dass die Sinus- und Kosinusfunktionen Perioden haben, die gleich $2\pi$ sind, d. h. wir haben $\sin(x + 2\pi) = \sin(x)$ und $cos(x + 2\pi) = cos(x)$ für jede $x$. Daraus ergibt sich im Einzelnen:

und:

Wir sehen also, dass $A$ und $D$ in der Phasenverschiebungs-Formel keine Auswirkung auf die Periode haben. In der Tat hängt alles davon ab, was innerhalb der trigonometrischen Funktionen passiert:

und:

Nach den gleichen Regeln wie oben ist der Wert nicht von $C$ abhängig. Da also drei Optionen verworfen werden, muss es die vierte sein: $B$.

Wir wenden uns wieder dem Kommentar zu, mit dem wir begonnen haben, um zu verstehen, warum und wie $B$ die Periodizität der Gleichungen der Phasenverschiebung $A \cdot \sin(Bx - C) + D$ und $A \cdot \cos(Bx - C) + D$ beeinflusst:

Mit jedem $2\pi/B$, das zu $x$ hinzugefügt wird, landen wir also wieder an der gleichen Stelle und die Funktion wiederholt sich (ähnlich verhält sich der Kosinus).

Die Periode einer Phasenverschiebung ist also gleich $2\pi/B$.

Unser tägliches Wissen über Wellen gibt normalerweise der Frequenz den Vorrang vor der Periode, aber das ist fast dasselbe. Entdecke in Omni's Frequenzrechner, warum das so ist.

Definitionsgemäß beschreibt die Phasenverschiebung die horizontale Verschiebung der Funktion in Bezug auf die reguläre $\sin(x)$- oder $\cos(x)$-Funktion. Bei den Grundfunktionen ist sie gleich $0$. Wenn wir ihre Graphen vergleichen, können wir feststellen, dass sie in der Tat gleich sind:

Wir stellen fest, dass wir das eine erhalten können, indem wir das andere übersetzen (in der Tat haben die gegenseitigen Funktionen viele Ähnlichkeiten):

und:

Das obige Beispiel zeigt bereits, wo wir auf $A \cdot\sin(Bx - C) + D$ und $A \cdot\cos(Bx - C) + D$ nach den Werten suchen sollten, die für die Phasenverschiebungen verantwortlich sind. Im Gegensatz zur Amplitude und der Periode brauchen wir dieses Mal jedoch zwei der vier Variablen.

Im Allgemeinen (d. h. nicht nur in Phasenverschiebungen) erhalten wir die horizontale Verschiebung einer beliebigen Funktion $f(x)$, indem wir $f(x - a)$ berechnen: die Verschiebung des Graphen um $a$ nach rechts. Mit anderen Worten: Wir ersetzen jedes Vorkommen von $x$ durch $x - a$ in der Formel für $f(x)$. Wendet man dies zum Beispiel auf $\sin(x)$ an, erhält man $\sin(x - a)$, aber für $\cos(3x + 1)$ würden wir z. B. dies erhalten:

Wir dürfen nicht die Multiplikatoren vergessen, die vor $x$ stehen.

In unserem Fall ergibt die Formel der Phasenverschiebung:

Das ist eine Phasenverschiebung $C/B$ (nach rechts) der Funktion $A \cdot\sin(Bx)$. Natürlich können wir das Obige auch für den Kosinus wiederholen.

Du musst also $C/B$ finden, um die Phasenverschiebung einer Phasenverschiebung-Gleichung zu berechnen.

Das ist einfach, vor allem, da wir jetzt gesehen haben, was die Phasenverschiebung, Amplitude und Periode sind und wie man sie berechnet. Lass uns auf das aufbauen, was wir bisher gelernt haben.

Wir wissen, dass in den Formeln für die Phasenverschiebung $A \cdot\sin(Bx - C) + D$ und $A \cdot\cos(Bx - C) + D$ das $A$ bestimmt, wie weit die Werte auf beiden Seiten der Mittelpunktlienie schwanken. $B$ gibt an, wie weit wir die Wellen des Graphen ausdehnen und wie schnell wir dadurch die Werte wiederholen können. Zusammen mit $C$ beschreiben die beiden Variablen außerdem, ob und wie weit wir die Funktion nach links oder rechts verschoben haben.

Natürlich hat die horizontale Verschiebung keinen Einfluss auf die vertikale Verschiebung: Schließlich handelt es sich um zwei senkrechte Richtungen. Die Amplitude hingegen sagt uns nur, wie weit der Graph vertikal reicht, aber sie verschiebt ihn nicht. Alles in allem bleibt uns nur ein Buchstabe: $D$.

$D$ in den Gleichungen zur Phasenverschiebung ist genau die vertikale Verschiebung. Sie bestimmt den Bereich der Funktion, d. h. wie weit wir den Graphen von der üblichen, nicht-$D$ Version wegbewegen.

Damit ist der theoretische Teil erst einmal abgeschlossen. Schauen wir uns die Berechnung der Phasenverschiebung an einem Beispiel an. Und weißt du was? Wir zeigen dir auch, wie du die Periode, die Amplitude und die vertikale Verschiebung berechnen kannst. Denn warum nicht? Mehr mathematische Berechnungen = mehr Spaß!

Schauen wir uns an, wie man die Amplitude, Periode, Phasenverschiebung und vertikale Verschiebung der Funktion $f(x) = 0,\!5 \cdot\sin(2x - 3) + 4$ findet. Zunächst lassen wir den Phasenverschiebung-Rechner arbeiten.

Oben in unserem Tool müssen wir die Funktion auswählen, die in unserer Formel vorkommt. In unserem Fall wählen wir „Sinus“ unter „Die trigonometrische Funktion in f“ aus. Das löst eine symbolische Darstellung einer solchen Phasenverschiebungsgleichung aus: $f(x) = A \cdot\sin(Bx - C) + D$. Wir geben dann Folgendes ein:

Beachte, dass der Phasenverschiebung-Rechner den Graphen der Funktion $\sin(x)$ anzeigt, noch bevor wir die Werte eingeben. Das liegt daran, dass das Tool freie Felder als keine Zahlen an den entsprechenden Stellen in der Formel versteht und folgende Standard-Werte einsetzt: $A = 1$, $B = 1$, $C = 0$ und $D = 0$, was bedeutet:

In dem Moment, in dem wir den letzten Wert eingeben, erscheint der Graph der Funktion darunter zusammen mit der Amplitude, der Periode, der Phasenverschiebung und der vertikalen Verschiebung. Beachte, dass du bei Bedarf in den erweiterten Modus des Rechners wechseln kannst, um den Wert der Funktion an einem beliebigen Punkt $x_0$ zu finden.

Lass uns jetzt klären, wie du die Phasenverschiebung und alle anderen Werte selbst ermitteln kannst. Dazu reicht es, wenn du dich an die vier obigen Abschnitte erinnerst, um Folgendes zu berechnen:

• Die Amplitude ist $A = 0,\!5$;
• Die Periode ist $2\pi / B = 2\pi / 2 = \pi$;
• Die Phasenverschiebung ist $C / B = 3 / 2 = 1,\!5$; und
• Die vertikale Verschiebung ist $D = 4$.

Die Grafik sieht dann so aus:

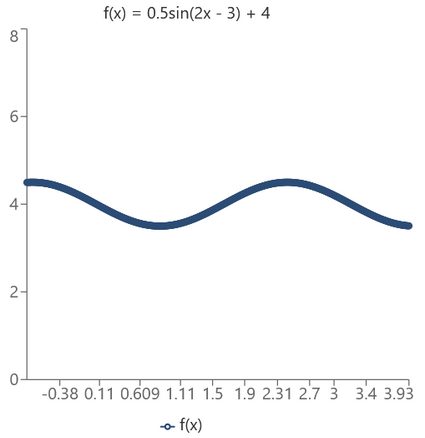
Ein Kinderspiel, nicht wahr? Experimentiere mit dem Phasenverschiebung-Rechner herum, um zu sehen, wie verschiedene Koeffizienten das Diagramm beeinflussen.

Um die Phasenverschiebung einer Funktion der Form A · sin(Bx - C) + D oder A · cos(Bx - C) + D zu berechnen, tue Folgendes:

1. Bestimme B.
2. Bestimme C.
3. Dividiere C/B.
4. Erinnere dich an Folgendes:
   • Positives Ergebnis: der Graph wird nach rechts verschoben.
   • Negatives Ergebnis: der Graph wird nach links verschoben.
5. Freu dich, denn du hast die Phasenverschiebung gefunden.

Um die Phasenverschiebung aus einem Diagramm zu ermitteln, tue Folgendes:

1. Bestimme, ob es sich um eine verschobene Sinus- oder Kosinusfunktion handelt.
2. Schau dir das Diagramm rechts von der vertikalen Achse an.
3. Finde den Ersten:
   • Hochpunkt, wenn der Koeffizient vor der Funktion positiv ist; oder
   • Tiefpunkt, wenn der Koeffizient negativ ist.
4. Berechne die Entfernung von der vertikalen Ursprungsgerade zu diesem Punkt.
5. Für Sinusfunktionen: Subtrahiere π/2 oder 3π/2 von dieser Entfernung für einen Hoch- bzw. Tiefpunkt.
6. Freu dich, dass du die Phasenverschiebung aus einem Graphen ermittelt hast.

Die Amplitude, Periode und Phasenverschiebung einer Funktion der Form A · sin(Bx - C) + D oder A · cos(Bx - C) + D lässt sich wie folgt bestimmen:

• Die Amplitude ist gleich A;
• Die Periode ist gleich 2π / B; und
• Die Phasenverschiebung ist gleich C / B.

Um trigonometrische Funktionen mit Phasenverschiebung grafisch darzustellen, tue Folgendes:

1. Bestimme die trigonometrische Funktion.
2. Fokussiere dich auf den Punkt (0,0) auf der Ebene.
3. Wenn die Phasenverschiebung:
   • Positiv ist, bewege dich nach rechts.
   • Negativ ist, bewege dich nach links.
4. Bewege dich um die Entfernung, die durch die Phasenverschiebung vorgegeben ist.
5. Der Punkt, an dem du landest, ist dein Startpunkt.
6. Zeichne den Graphen der nicht verschobenen Funktion, als ob der Punkt (0,0) wäre.
7. *Prima, du hast nun eine trigonometrische Funktion mit einer Phasenverschiebung gezeichnet.

Wenn es um trigonometrische Funktionen geht, ja. Der Begriff „Phasenverschiebung“ wird normalerweise für trigonometrische Funktionen verwendet. Mit anderen Worten: Eine horizontale Verschiebung kann bei jedem Graphen oder jeder Funktion auftreten. Wenn es sich jedoch um eine trigonometrische Funktion handelt, können wir diese horizontale Verschiebung auch Phasenverschiebung nennen.