Rolling Offset Rechner

Q: Wie berechne ich den Weg eines Rohrs?

So findest du den Weg eines Rohrs: Miss den horizontalen Versatz, den vertikalen Versatz und den Lauf des Rohrversatzes. Quadriere jede dieser Messungen und addiere sie dann alle zusammen . Ziehe die Quadratwurzel aus der Summe , um den Weg zu erhalten. Wenn du den Wert des Laufs nicht kennst oder einen bevorzugten Biegewinkel für das Fitting hast, wiederhole die Schritte 2 und 3, wobei der Lauf gleich null ist, und dividiere alles durch den Sinus des Biegewinkels deines Fittings. Read more

Created by Kenneth Alambra

Reviewed by Wojciech Sas, PhD and Steven Wooding

Translated by Luise Schwenke and Julia Kopczyńska, PhD candidate

Last updated: Jan 18, 2024

Table of contents:

Mit dem Rohrversatz-Rechner (Rolling Offset) kannst du den Weg ermitteln, der für den erforderlichen Rohrversatz für typische Rohrfitting-Bögen oder jeden beliebigen Biegewinkel benötigt wird.

In diesem Rechner erfährst du:

Was Rolling Offset ist;
Die verschiedenen Formeln für den Rolling Offset; und
Wie man den Rolling Offset berechnet.

Du wirst auch über die verschiedenen Begriffe lesen, die wir normalerweise verwenden, wenn es um Rohrverschiebung geht, wie wahrer Versatz, Weg und Lauf. Außerdem zeigen wir dir eine Rohrverschiebungstabelle mit Rohrverschiebungsmultiplikatoren, mit denen du die Länge des Weges schnell und einfach ermitteln kannst.

Was ist ein Rohrversatz? Was ist ein Rolling Offset?

Bei der Durchführung von Rohrleitungsarbeiten kommt es manchmal zu Situationen, in denen wir zwei Rohrleitungen verbinden müssen, die nicht ganz zueinander ausgerichtet sind. Diese beiden Rohrleitungen können horizontal oder vertikal versetzt sein. Wenn es sich um eine Kombination aus horizontalem und vertikalem Versatz handelt oder um eine Kombination aus Versätzen in zwei verschiedenen Richtungen, sprechen wir von einem Rohrversatz.

Um mit Rohrverschiebungen umzugehen, können wir eine gebogene Rohrverschraubung verwenden, um die Richtung der Rohrleitung zu ändern, und eine weitere gebogene Verschraubung, um zur endgültigen Richtung der Rohrleitung zurückzukehren. In diesem Rechner geht es um die Ermittlung der Weglänge, welche die Länge der Diagonalen ist, die die beiden Punkte verbindet, an denen die Rohrleitung ihre Richtung ändert, wie in der Abbildung unten dargestellt:

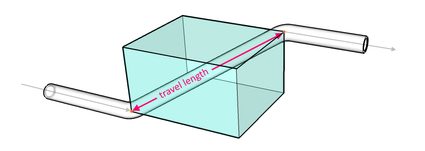
Einfaches Rohrleitungsdiagramm, das die zwei verschiedenen Biegestellen einer Rohrleitung und den Weg der Rohrverdrängung zeigt.

Die Länge des Weges hängt von den horizontalen und vertikalen Versätzen und dem verwendeten gebogenen Rohrfitting ab. Wir können die Länge des Weges mithilfe der Trigonometrie, einigen Konzepten von rechtwinkligen Dreiecken und dem Satz des Pythagoras berechnen. Bevor wir mit der Berechnung des Rohrversatzes fortfahren, lass uns zunächst lernen, wie wir den Rolling-Offset-Rechner benutzen.

Wie verwende ich den Rolling-Offset-Rechner?

Die Verwendung unseres Rolling-Offset-Rechners ist mühelos, da du dafür keine Formel kennen musst. Unser Tool hilft dir auch dabei, mit Diagrammen, die sich je nach deiner Auswahl und deinen Eingaben ändern, zu visualisieren, wie dein Rohrversatz aussieht. Hier sind die Schritte, die du befolgen kannst, um unseren Rechner zu benutzen:

Gib sowohl den horizontalen als auch den vertikalen Versatz ein, den du für deine Rohrleitung benötigst. Unser Rohrversatz-Rechner zeigt dir sofort den wahren Versatz deiner Rohrleitung an.
Wähle dann den bevorzugten Fittingbogen, je nachdem, welcher dir zur Verfügung steht. Wähle Benutzerdefiniert, wenn du dein eigenes Rohr biegst oder wenn du individuell gebogene Rohrformstücke hast.
Wenn du bei der Auswahl des Fittingbogens die Option Benutzerdefiniert gewählt hast, zeigt unser Tool die Variable Biegewinkel der Fittings an, in die du deinen gewünschten Biegewinkel eingeben kannst.
Wenn du deinen Fittingbogen auswählst oder eingibst, siehst du die Länge des Wegs und die Länge des Laufs, den deine Rohrleitung zurücklegen muss, um deinen Rohrversatz fertigzustellen.

Im nächsten Abschnitt dieses Textes werden wir lernen, wie wir den Rohrversatz selbst berechnen können, um besser zu verstehen, wie unser Rechner funktioniert.

Wie berechne ich den Rohrversatz?

Um einen Rohrversatz in einer Rohrleitung zu berechnen, musst du zwei Hypotenusen zweier rechtwinkliger Dreiecke innerhalb des imaginären Quaders finden, den ein Rohrversatz bildet. Wir haben einen separaten Hypotenuse Rechner und einen Rechtwinkliges Dreieck Rechner, wenn du tiefer in diese Themen eintauchen möchtest.

In der folgenden Abbildung sehen wir, dass wir die horizontalen und vertikalen Versatzmaße als die Schenkel eines rechtwinkligen Dreiecks betrachten können, und seine Hypotenuse der wahre Versatz der Pipeline ist:

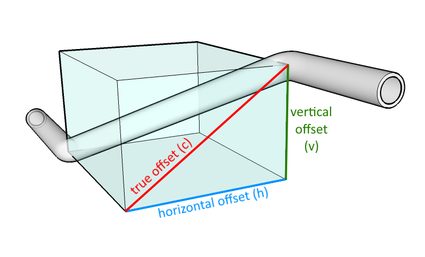
Das Bild zeigt das erste rechtwinklige Dreieck, die Horizontale, die Vertikale und den wahren Versatz.

Mithilfe des Satzes des Pythagoras können wir den Wert des wahren Versatzes $c$ , der einfach die Diagonale eines Rechtecks ist, mit der folgenden Gleichung bestimmen:

c = \sqrt{h^2 + v^2},

wobei:

$c$ — Echter Versatz der Rohrleitung;
$h$ — Horizontaler Versatz der Rohrleitung; und
$v$ — Vertikaler Versatz der Rohrleitung.

Werfen wir nun einen Blick in den imaginären Quader, um ein weiteres rechtwinkliges Dreieck zu sehen, das durch den wahren Versatz, den Lauf und die Lauflänge gebildet wird:

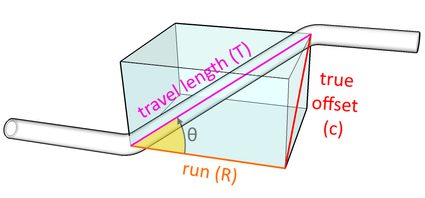
Das Bild zeigt das zweite rechtwinklige Dreieck und den Weg als Hypotenuse.

In diesem Dreieck können wir den Satz des Pythagoras nicht anwenden, da wir zunächst den Wert des Laufs $R$ nicht kennen, den wir benötigen, um die Länge des Weges $T$ zu erhalten. Da wir jedoch den Biegewinkel des Rohrformstücks kennen, das wir verwenden möchten, können wir die trigonometrische Funktion 🇺🇸 des Sinus verwenden, um den Wert von $T$ zu erhalten:

T = \frac{c}{sin(\theta)},

wobei:

$T$ — Länge des Weges der Rohrleitung, die die beiden gegenüberliegenden Ecken unserer imaginären Box verbindet;
$c$ — Echter Versatz der Rohrleitung; und
$\theta$ — Biegewinkel des Rohrfittings, den du verwenden wirst.

Mithilfe des Satzes des Pythagoras kannst du dann die Länge des Laufs mit dieser Gleichung ermitteln:

R = \sqrt{T^2 - c^2},

oder die trigonometrische Funktion einer Tangente:

R = \frac{c}{\tan(\theta)}.

Abgesehen von diesen Gleichungen ist es auch erwähnenswert, dass du, wenn du den Wert des Laufs bereits kennst, zusammen mit den Werten der horizontalen und vertikalen Versätze auch direkt den Wert von $T$ mit dieser Gleichung erhalten kannst:

T = \sqrt{R^2 + h^2 + v^2}.

Da wir nun alle Gleichungen kennen, die wir für die Berechnung von Rolling Offset-Messungen benötigen, betrachten wir nun ein Beispiel 🙂

Wie macht man einen 45-Grad-Rohrversatz? Beispielrechnung

Nehmen wir an, wir möchten zwei Rohrleitungen verbinden, die horizontal und vertikal um einen Meter (100 cm) bzw. einen halben Meter (50 cm) versetzt sind. In diesem Fall wollen wir 45-Grad-Rohrbögen verwenden, um den Rohrversatz herzustellen. Wie machen wir also diesen 45-Grad-Rohrversatz? Wir können damit beginnen, den tatsächlichen Versatz der Rohrleitung mithilfe unserer Gleichung zu ermitteln:

\begin{align*} c &= \sqrt{h^2 + v^2}\\[0.5em] &= \sqrt{100^2 + 50^2}\\[0.5em] &= \sqrt{10\hspace{0.5mm}000 + 2\hspace{0.5mm}500}\\[0.5em] &= \sqrt{12\hspace{0.5mm}500}\\[0.5em] &= 111,\!80\ \text{cm} \end{align*}

Wenn wir unsere Gleichung zur Lösung der Weglänge verwenden, ergibt sich:

\begin{align*} T &= \frac{c}{sin(\theta)}\\[1.2em] &= \frac{111,\!80\ \text{cm}}{sin(45\degree)}\\[1.2em] &= 158,\!11\ \text{cm} \end{align*}

Die Länge des Laufs können wir dann mit einer der beiden zuvor besprochenen Gleichungen ermitteln. In diesem Beispiel verwenden wir die Gleichung mit der Tangensfunktion wie folgt:

\begin{align*} R &= \frac{c}{\tan(\theta)}\\[1.2em] &= \frac{111,\!80\ \text{cm}}{\tan(45\degree)}\\[1.2em] &= 111,\!80\ \text{cm} \end{align*}

Wir kennen jetzt die notwendigen Abstände, um den Rohrversatz unserer Pipeline mit den von uns durchgeführten Berechnungen zu vervollständigen. Beachte außerdem, dass der Lauf immer gleich dem wahren Versatz ist, wenn wir 45-Grad-Bögen verwenden. Bei anderen Rohranschlusswinkeln werden die Werte bereits anders sein.

💡 Beachte jedoch, dass du die Länge entsprechend deiner Fittingzugaben anpassen musst, um die notwendige Rohrlänge für die perfekte Montage deiner Rohrleitung zu bestimmen.

Wie berechne ich schnell den Rohrversatz? Die Verwendung von Rohrversatz-Multiplikatoren

Eine andere Möglichkeit, die Weglänge zu bestimmen, ist die Verwendung einiger konstanter Rohrversatz-Multiplikatoren. Diese Konstanten sind vor allem dann nützlich, wenn du die Weglängen selbst berechnen möchtest, aber nur einen Taschenrechner hast, der keine trigonometrischen Funktionen hat. Wir haben diese Konstanten in der unten stehenden Tabelle für den Rohrversatz zu deiner Information aufgeführt:

Biegewinkel	Multiplikator
22 ½°	2,6131
45°	1,4142
60°	1,1547
90°	1,0000

Um einen Rohrversatzmultiplikator zu verwenden, musst du jedoch zunächst den wahren Versatz ermitteln. Um die Länge zu ermitteln, musst du dann die Konstante mit dem tatsächlichen Versatz multiplizieren, wie in der folgenden Gleichung dargestellt:

T = m\cdot \sqrt{h^2 + v^2},

dabei ist $m$ der Rohrversatzmultiplikator.

✅ Wenn dich das Berechnen von Winkeln in der Welt des Bauwesens genauso interessiert wie die Rohrversatz-Berechnungen, dann könnten dir auch unser Schrägschnitt Rechner 🇺🇸 und unser Gehrungswinkel Rechner gefallen. 😊

FAQ

Was ist ein Rolling Offset?

Wenn wir eine Rohrleitung in horizontaler und vertikaler Richtung versetzen müssen, haben wir ein Rolling Offset (Rohrversatz). Stell dir eine Rohrleitung vor, die in eine Ecke eines imaginären Kastens eintritt und an der am weitesten gegenüberliegenden diagonalen Ecke des besagten imaginären Kastens wieder austritt. Du kannst einen Rolling Offset schließen, indem du die Weglänge der Rohrleitung ermittelst.

Wie berechne ich den Rolling Offset in Rohrleitungen?

So berechnest du den Rolling Offset in Rohrleitungen:

Miss den horizontalen und vertikalen Versatz des Rolling Offset.
Bestimme den wahren Versatz, der die Hypotenuse des rechtwinkligen Dreiecks ist, das durch diese Versätze gebildet wird.
Dividiere den wahren Versatz durch den Sinus des Biegewinkels des Fittings, um die Weglänge zu ermitteln.
Außerdem kannst du den wahren Versatz durch den Tangens des Biegewinkels deines Fittings teilen, um den Lauf des Rohrversatzes zu schätzen.

Wie berechne ich ein Rolling Offset von 45?

So ermittelst du einen Rohrversatz mithilfe von 45-Grad-Bögen:

Bestimme den horizontalen und vertikalen Versatz deiner Rohrleitung.
Ziehe die Quadratwurzel aus der Summe der Quadrate des horizontalen und vertikalen Versatzes. Dies ist der wahre Versatz deines Rolling Offsets.
Schließlich multiplizierst du den wahren Versatz mit 1,4142 oder dividierst den wahren Versatz durch sin(45°).

Wie klebe ich PVC-Rohrverbindungen?

Die beste Art, PVC-Rohrformstücke auf Rohre zu kleben, ist die Verwendung von PVC-Zementkleber. PVC-Zementkleber schmelzen vorübergehend die Oberflächen der PVC-Materialien, auf die du sie aufträgst. Während die PVC-Oberflächen schmelzen, kannst du sie miteinander in Kontakt bringen, damit sie beim Trocknen eine chemische Verbindung eingehen. Achte darauf, das Rohr und den Fitting ein wenig zu verdrehen, um eine richtig dichte Verbindung zu gewährleisten, wenn du PVC-Zementkleber verwendest.

Wie berechne ich den Weg eines Rohrs?

So findest du den Weg eines Rohrs:

Miss den horizontalen Versatz, den vertikalen Versatz und den Lauf des Rohrversatzes.
Quadriere jede dieser Messungen undaddiere sie dann alle zusammen.
Ziehe die Quadratwurzel aus der Summe, um den Weg zu erhalten.
Wenn du den Wert des Laufs nicht kennst oder einen bevorzugten Biegewinkel für das Fitting hast, wiederhole die Schritte 2 und 3, wobei der Lauf gleich null ist, und dividiere alles durch den Sinus des Biegewinkels deines Fittings.

Wie groß ist der Weg eines 30x30 cm großen 45-Grad-Rolling Offsets?

So ermittelst du die Weglänge eines Rolling Offsets mit 30 cm horizontalem Versatz und 30 cm vertikalem Versatz unter Verwendung eines um 45 Grad gebogenen Fittings:

Quadriere die horizontalen und vertikalen Versätze und addiere sie wie folgt: 30² + 30² = 1800.
Berechne die Quadratwurzel, um den wahren Versatz zu ermitteln: √1800 = 42,43 cm.
Schließlich teilst du 42,43 cm durch den Sinus von 45° und erhältst 42,43 cm/sin (45°) = 60 cm.

Kenneth Alambra

The illustration of a pipe section with a rolling offset while showing its corresponding dimensions.

Roll or horizontal offset (h)

Set or vertical offset (v)

True offset (c)

Fitting bend

Travel (T)

Run (R)

Aluminum weightBalusterBoard and batten… 31 more