Calculadora de Progressão Geométrica

Q: Como calcular a razão de uma sequência geométrica?

Para calcular a razão de uma sequência geométrica, divida quaisquer dois termos consecutivos da sequência.

Created by Álvaro Díez and Anna Szczepanek, PhD

Reviewed by Bogna Szyk and Jack Bowater

Translated by Marinara Andrade do Nascimento Moura, PhD candidate, Luna Maldonado Fontes and João Rafael Lucio dos Santos, PhD

Last updated: Oct 30, 2024

Table of contents:

Com a nossa calculadora de sequência geométrica, você pode calcular tudo e qualquer coisa sobre uma sequência, ou progressão geométrica. Essa calculadora de séries geométricas o ajudará a entender a definição de sequência geométrica, para que você possa responder à pergunta: o que é uma sequência geométrica?

Explicamos a você a diferença entre as duas equações de sequência geométrica, a fórmula explícita e recursiva para uma sequência geométrica e como usar a fórmula de sequência geométrica com alguns exemplos interessantes.

Também criamos uma função de "calculadora de séries geométricas" que avaliará a soma de uma sequência geométrica, começando pela fórmula explícita de uma sequência geométrica e construindo, passo a passo, a fórmula da série geométrica.

Definição de sequência geométrica

A sequência ou progressão geométrica é uma coleção de números, na qual todos, exceto o primeiro, são obtidos multiplicando-se o anterior por um número fixo, diferente de zero, chamado de razão. Essa definição também é utilizada para a progressão geométrica, que nada mais é do que uma sequência numérica que possui uma razão fixa. Se você estiver com dificuldades para entender o que é uma sequência geométrica, não se preocupe! Mais adiante, explicaremos o que isso significa em termos mais simples e veremos as fórmulas recursiva e explícita de uma sequência geométrica. Também incluímos alguns exemplos de sequências geométricas.

Antes de analisarmos a definição corretamente, é importante esclarecer alguns pontos para evitar confusão. Em primeiro lugar, precisamos entender que, embora a progressão geométrica seja composta pela multiplicação constante de números por um fator, isso não está relacionado ao fatorial, consulte a calculadora de fatorial 🇺🇸 da Omni). Na verdade, isso está relacionado ao Máximo Divisor Comum (MDC) e ao Mínimo Múltiplo Comum (MMC), pois todos os números da sequência compartilham um MDC ou um MMC, desde que o primeiro número dessa sequência seja um número inteiro.

Isso significa que o MDC (consulte a Calculadora de MDC - Máximo Divisor Comum da Omni) é simplesmente o menor número na sequência. Por outro lado, o MMC é simplesmente o maior dos números na sequência. Por exemplo, na sequência 3, 6, 12, 24, 48, o MDC é 3 e o MMC é 48. Mas se considerarmos apenas os números 6, 12, 24, o MDC seria 6 e o MMC seria 24.

Progressão geométrica: O que é uma progressão geométrica?

Agora, vamos ver o que é uma sequência geométrica em termos mais simples. Uma sequência geométrica é uma coleção de números específicos que estão relacionados por uma razão, como já mencionamos anteriormente. Essa razão é uma das características definidoras de uma determinada sequência, juntamente com o termo inicial da sequência. Veremos mais adiante como esses dois números estão na base da definição da sequência geométrica e como, dependendo de como são usados, é possível obter a fórmula explícita de uma sequência geométrica ou a fórmula recursiva equivalente para a sequência geométrica.

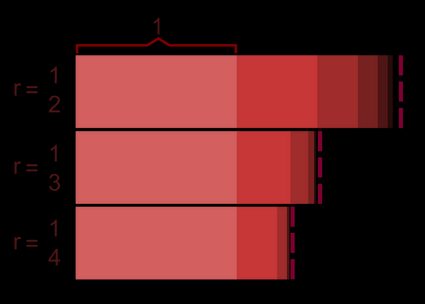
Exemplos de sequências geométricas com proporções de 1/2, 1/3, 1/4 e o termo inicial de 1. — Exemplos de sequências geométricas com diferentes proporções

Agora, vamos construir uma sequência geométrica simples usando valores concretos para esses dois parâmetros definidos. Para simplificar, consideraremos o termo inicial como $1$ e a razão será definida como $2$ . Nesse caso, o primeiro termo será $a_1 = 1$ . Por definição, o segundo termo será $a_2 = a_1 ⋅ 2 = 2$ , o terceiro termo será $a_3 = a_2 ⋅ 2 = a_1 ⋅ 2^2 = 4$ , etc. O enésimo termo da progressão seria então:

a_{n} = 1 \cdot 2^{{n}-1}

onde $n$ é a posição do referido termo na sequência.

Como você pode ver, a razão de quaisquer dois termos consecutivos da sequência, definida exatamente como descrito no texto da calculadora de razão da Omni, é constante.

Uma maneira comum de escrever uma progressão geométrica é escrever explicitamente os primeiros termos. Isso permite que você calcule qualquer outro número na sequência. Para o nosso exemplo, escreveríamos a série como:

1, 2, 4, 8, ...

No entanto, há outras maneiras matemáticas de fornecer as mesmas informações. Essas outras formas são as chamadas fórmula explícita e recursiva para sequências geométricas. Agora que entendemos o que é uma sequência geométrica, podemos nos aprofundar nessa fórmula e explorar maneiras de transmitir as mesmas informações em menos palavras e com maior precisão.

Fórmulas recursiva e explícita para a sequência geométrica

Existem duas maneiras distintas pelas quais você pode representar matematicamente uma sequência geométrica: a fórmula explícita para uma sequência geométrica e a fórmula recursiva para uma sequência geométrica. A primeira delas é a que já vimos em nosso exemplo de série geométrica. O que vimos foi a fórmula específica e explícita para esse exemplo, mas você pode escrever uma fórmula que seja válida para qualquer progressão geométrica, ou seja, você pode substituir os valores de $a_1$ pelo termo inicial correspondente e $r$ pela razão. A fórmula geral para o enésimo termo é:

a_{n} = a_{1}r^{{n}-1}, n \in \mathbb N

onde $n \in \mathbb N$ significa que $n = 1, 2, 3, ... , n$ . A fórmula do termo geral para sequências geométricas transmite as informações mais importantes sobre uma progressão geométrica: o termo inicial $a_1$ , como obter qualquer termo a partir do primeiro e o fato de que não há termo antes do inicial.

Há outra maneira de mostrar as mesmas informações usando outro tipo de fórmula: a fórmula recursiva para uma sequência geométrica. Ela é composta de duas partes que transmitem informações diferentes da definição da sequência geométrica. A primeira parte explica como você pode ir de qualquer termo da sequência para qualquer outro termo usando a proporção. Esse significado por si só não é suficiente para construir uma sequência geométrica do zero, pois não sabemos o ponto de partida. Essa é a segunda parte da fórmula, o termo inicial (ou qualquer outro termo, nesse caso). Vamos ver como essa fórmula recursiva se parece:

\begin{align*} a_{n} &= a_{n-1} \cdot r \\ a_{i} &= x \end{align*}

onde $x$ é usado para expressar que qualquer número será usado em seu lugar, mas também que deve ser um número explícito e não uma fórmula. O subscrito $i$ indica qualquer número natural (assim como $n$ ), mas é usado no lugar de $n$ para deixar claro que $i$ não precisa ser o mesmo número que $n$ .

Como usar a calculadora de sequência geométrica?

Agora que você sabe o que é uma sequência geométrica e como escrevê-la tanto na fórmula recursiva quanto na explícita, é hora de aplicar seu conhecimento e calcular algumas coisas! Com a nossa ferramenta, você pode calcular todas as propriedades das sequências geométricas, como a razão, o termo inicial, o enésimo termo, o último termo, etc. Aqui está uma breve descrição de como a calculadora está estruturada:

Primeiro, diga-nos o que você sabe sobre sua sequência escolhendo:
- a razão e o primeiro termo da sequência;
- a razão e algum enésimo termo; ou
- dois termos quaisquer;
Insira seus dados. Com base nisso, a calculadora determina toda a sua sequência geométrica.
Por padrão, a calculadora exibe os primeiros cinco termos da sequência. Você pode alterar os termos inicial e final de acordo com suas necessidades.

Nossa ferramenta também pode calcular a soma de sua sequência: toda ela ou apenas parte dela. No último caso, basta inserir o ponto inicial e final da soma e você poderá aproveitar o resultado. Como você aprenderá nas próximas seções, a soma infinita pode não existir!

Fórmula da série geométrica: a soma de uma sequência geométrica

Até agora, falamos sobre sequências geométricas ou progressões geométricas, que são coleções de números. No entanto, há resultados realmente interessantes a serem obtidos quando você tenta somar os termos de uma sequência geométrica. Quando temos uma progressão geométrica finita, com um número limitado de termos, o processo aqui é tão simples quanto encontrar a soma de uma sequência numérica linear. O cálculo da soma dessa sequência geométrica pode até ser feito manualmente, teoricamente.

Mas podemos ser mais eficientes do que isso usando a fórmula da série geométrica e brincando com ela. Para fazer isso, usaremos o sinal matemático de soma $\Sigma$ , o que significa somar todos os termos depois dele. Por exemplo, se tivermos uma progressão geométrica chamada a_n e nomearmos a soma da sequência geométrica S, a relação entre ambas seria:

\scriptsize S = \sum_{n=1}^m a_{n} = a_{1} + a_{2} + a_{3} + ... + a_m

se quisermos somar os primeiros m termos, ou:

\scriptsize S = \sum_{n=1}^\infty a_{n} = a_{1} + a_{2} + a_{3} + \ldots

se quisermos somar todos os termos.

Infelizmente, isso ainda deixa você com o problema de realmente calcular o valor da série geométrica. Você sempre pode usar essa calculadora como uma calculadora de séries geométricas, mas seria muito melhor se, antes de usar qualquer calculadora de soma geométrica, você entendesse como fazer isso manualmente. Há um truque que pode tornar nosso trabalho muito mais fácil e envolve ajustar e resolver a equação da sequência geométrica da seguinte forma:

\scriptsize \begin{align*} S &= \sum_{n=1}^m a_{n} \\ &= a_{1} + a_{1}r + a_{1}r^2 + ... + a_{1}r^{m-1} \end{align*}

Agora, multiplique ambos os lados por $(1-r)$ e resolva:

\scriptsize \begin{align*} S (1 - r) &= (1 - r) (a_1 + a_1r + a_1r^2 + \ldots\\ &\hspace{4em}+\ a_1r^{m-1}) \\[1.5em] \end{align*} \\ \begin{align*} S(1-r) &= a_1 + a_1r + ... + a_1r^{m-1} \\ &\hspace{1em} -(a_1r + a_1r^2 + \ldots + a_1r^{m}) \\[.5em] &= a_1 - a_1r^{m} \end{align*}

\scriptsize S = \sum_{n=1}^m a_{n} = a_1 - a_1 \frac{r^{m}}{1-r} = a_1 \frac{1-r^m}{1-r}

Você pode calcular facilmente esse resultado por conta própria e ele representa a fórmula básica da série geométrica quando o número de termos na série é finito. Entretanto, estamos falando de matemática e não da vida real, portanto, podemos ter um número infinito de termos em nossa série geométrica e ainda assim calcular a soma total de todos os termos. Como essa mágica funciona? Calma que nós te explicaremos todos os detalhes que você precisa saber.

Usando a fórmula da sequência geométrica para calcular uma soma infinita

Depois de ver como obter a fórmula da série geométrica para um número finito de termos, é natural (pelo menos para os matemáticos) perguntar como posso calcular a soma infinita de uma sequência geométrica? Pode parecer impossível fazer isso, mas alguns truques nos permitem calcular esse valor em algumas etapas simples. Para isso, precisamos introduzir o conceito de limite. Esse é um processo matemático pelo qual podemos entender o que acontece no infinito. Ele também pode ser usado para tentar definir matematicamente expressões que normalmente não são definidas, como "zero dividido por zero" ou "zero elevado à potência de zero".

Falar sobre limites é um assunto muito complexo e está além do escopo desta calculadora. Sua complexidade é a razão pela qual decidimos apenas mencioná-los e não entrar em detalhes sobre como calculá-los. Mas não se preocupe, pois você pode encontrar excelentes informações sobre limites na internet, como, por exemplo, no site da Wikipédia.

Mesmo que você não se dê ao trabalho de verificar o que são os limites, você ainda pode calcular a soma infinita de uma série geométrica usando nossa calculadora. A única coisa que você precisa saber é que nem toda série tem uma soma definida. As condições que uma série precisa atender para que sua soma seja um número (isso é o que os matemáticos chamam de convergência) são, em princípio, simples. Nós as explicamos na seção a seguir.

Observações sobre o uso da calculadora como uma calculadora de séries geométricas

Quando se trata de séries matemáticas (sequências geométricas e aritméticas), elas geralmente são agrupadas em duas categorias diferentes, dependendo da soma dos termos da série ser finita (série convergente) ou infinita/não definida (série divergente). A melhor maneira de saber se uma série é convergente ou não é calcular sua soma infinita usando limites. Além disso, existem alguns truques que podem nos permitir distinguir rapidamente entre as séries convergentes e divergentes sem precisar fazer todos os cálculos. Esses truques incluem: observar o termo inicial, o termo geral da sequência e a sua proporção, ou ainda, comparar com outras séries.

Visualização da soma de uma sequência geométrica com um termo inicial de 1 e uma razão de 1/2 na forma da área de um retângulo dividido em retângulos cada vez menores. — Visualização da soma de uma sequência geométrica

Para que uma série seja convergente, o termo geral $a_n$ deve ficar menor a cada aumento no valor de $n$ . Se $a_n$ ficar menor, não podemos garantir que a série será convergente, mas se $a_n$ for constante ou ficar maior à medida que aumentarmos $n$ , podemos dizer com certeza que a série será divergente. Se não tivermos certeza se $a_n$ fica menor, podemos observar o termo inicial e a razão, ou até mesmo calcular alguns dos primeiros termos. Isso nos dará uma ideia de como $a_n$ evolui.

A segunda opção que temos é comparar a evolução de nossa progressão geométrica com uma que sabemos com certeza que converge (ou diverge), o que pode ser feito com uma rápida pesquisa on-line. Em termos gerais, se a série que estamos investigando for menor (ou seja, $a_n$ for menor) do que uma que sabemos com certeza que converge, podemos ter certeza de que nossa série também convergirá. Por outro lado, se nossa série for maior do que uma série que sabemos com certeza que é divergente, nossa série sempre divergirá. Nos demais casos (maior que uma convergente ou menor que uma divergente), não podemos dizer nada sobre nossa série geométrica e somos forçados a encontrar outra série para comparar ou usar outro método.

Esses critérios se aplicam às progressões aritméticas e geométricas. De fato, essas duas estão intimamente relacionadas entre si e ambas as sequências podem ser vinculadas pelas operações de exponenciação e obtenção de logaritmos.

O paradoxo de Zenão e outros exemplos de sequências geométricas

Já vimos um exemplo de sequência geométrica na forma da chamada Sequência de potências de dois. Essa é uma sequência muito importante por causa dos computadores e sua representação binária de dados. Nessa progressão, podemos encontrar valores como o número máximo permitido em um computador (varia de acordo com o tipo de variável que usamos), o número de bytes em um gigabyte ou o número de segundos até o fim do tempo do UNIX (valores originais e corrigidos).

Além da sequência de potências de dois, podemos ter qualquer outra sequência de potências se simplesmente substituirmos $r = 2$ pelo valor da base na qual estamos interessados. As séries de potências são comumente usadas e amplamente conhecidas e podem ser expressas usando a conveniente fórmula da sequência geométrica. Mas essas sequências de potências de qualquer tipo não são as únicas sequências que podemos ter, e mostraremos a você progressões geométricas ainda mais importantes ou interessantes, como a série alternada ou o surpreendente paradoxo de Zenão.

Vamos começar com os paradoxos de Zenão, em particular, o chamado Paradoxo da dicotomia. Esse paradoxo é, em sua essência, apenas um quebra-cabeça matemático na forma de uma série geométrica infinita. Zenão foi um filósofo grego que antecedeu Sócrates. Ele criou um mecanismo pelo qual poderia provar que o movimento era impossível e nunca deveria acontecer na vida real. A ideia é dividir a distância entre o ponto de partida (A) e o ponto de chegada (B) pela metade. Depois de percorrer a primeira metade, você divide a distância restante pela metade novamente... Você pode repetir esse processo quantas vezes quiser, o que significa que sempre terá alguma distância restante para chegar ao ponto B.

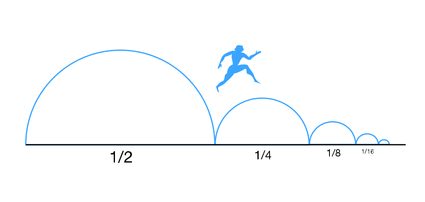
Paradoxo de Zenão (dicotomia) visualizado. O velocista grego corre 1/2 do comprimento da distância anterior a cada vez, nunca completando a corrida. — Paradoxo de Zenão (dicotomia) visualizado.

O paradoxo da dictomia parece prever que, como temos um número infinito de metades para caminhar, precisaríamos de uma quantidade infinita de tempo para viajar de A a B. No entanto, como sabemos por nossa experiência cotidiana, isso não é verdade, e sempre podemos ir do ponto A ao ponto B em um tempo finito (exceto para algumas pessoas que parecem chegar infinitamente atrasados em todos os lugares). A solução para esse aparente paradoxo pode ser encontrada usando a matemática.

Se expressarmos o tempo que você leva para ir de A a B (vamos chamá-lo de $t$ por enquanto) na forma de uma série geométrica, teremos uma série definida por: $a_1 = t/2$ com a razão comum sendo $r = 1/2$ . Portanto, a primeira metade levaria $t/2$ para ser percorrida, depois cobriríamos metade da distância restante em $t/4$ , depois $t/8$ , etc... Se agora realizarmos a soma infinita da série geométrica, descobriremos que:

\scriptsize\begin{align*} S &= \sum_{n=1}^\infty a_n = \frac{t}{2} + \frac{t}{4} + ... \\[1em] &= t ⋅ \left(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...\right) = t ⋅ 1 = t \end{align*}

Essa é a prova matemática de que podemos ir de A a B em um período de tempo finito ( $t$ nesse caso).

Para finalizar, e caso o paradoxo da dictomia de Zenão não tenha sido uma experiência suficientemente surpreendente, vamos mencionar a série de unidades alternadas, ou, simplesmente, série alternada.

Essa série começa em $a_1 = 1$ e tem uma razão $r = -1$ que produz uma série da forma:

\scriptsize S = \sum_{n=1}^\infty a_n = 1 - 1 + 1 - 1 + ...

Isso não converge conforme os critérios padrão, pois o resultado depende do número de termos ser par ( $S = 0$ ) ou ímpar ( $S = 1$ ). No entanto, há um truque pelo qual podemos "fazer" essa série convergir para um número finito. O truque em si é muito simples, mas é baseado em argumentos matemáticos muito complexos, portanto, não se arrisque a mostrar isso a um matemático, pois você poderá ter grandes problemas. Vamos ver a "solução":

\scriptsize S = 1 - 1 + 1 - 1 + ...

Multiplicamos ambos os lados por $-1$ :

\scriptsize\begin{align*} -S &= -1 + 1 - 1 + 1 - ... \\[1em] &= -1 + (1 - 1 + 1 - 1 + ...) \\[1em] &= -1 + S \end{align*}

Resolvendo para $S$ , temos:

\scriptsize -S - S = -1 → 2S = 1 → S = 1/2

Agora você pode se exibir para seus amigos (desde que eles não sejam matemáticos).

FAQ

O que é a sequência geométrica?

Uma sequência geométrica é uma série de números em que o próximo termo é obtido pela multiplicação do termo anterior por um termo comum, a razão.

Como encontrar a soma de uma sequência geométrica?

Para encontrar a soma de uma sequência geométrica:

Calcule a razão, r elevado à potência n.
Subtraia a resultante rⁿ de 1.
Divida a resultante por (1 - r).
Multiplique a resultante pelo primeiro termo, a₁.

Como encontrar o enésimo termo de uma sequência geométrica?

Para encontrar o enésimo termo de uma sequência geométrica:

Calcule a razão elevada à potência (n - 1).
Multiplique a resultante pelo primeiro termo, a.

Como calcular a razão de uma sequência geométrica?

Para calcular a razão de uma sequência geométrica, divida quaisquer dois termos consecutivos da sequência.

Álvaro Díez and Anna Szczepanek, PhD

Formula to find the n-th term of the geometric sequence:

Type

Common ratio r

a₁

Here's your sequence

Starting from term no.

Up to term no.

a₁ =

a₂ =

a₃ =

a₄ =

a₅ =

Summing the sequence

Find

a₁ + a₂ + a₃ + ... =

To increase the precision of calculations, go to the advanced mode.

Arithmetic sequenceCollatz conjectureConvolution… 7 more