Calculadora de Hexágonos

Esta é a calculadora de hexágonos, uma ferramenta útil para realizar cálculos relacionados a um hexágono regular. O formato hexagonal é um dos mais populares na natureza. Seus usos são quase infinitos, sendo encontrados desde padrões de favo de mel até ladrilhos hexagonais para espelhos. Aqui explicamos não apenas porque o polígono de 6 lados é tão popular, mas também como desenhar os lados do hexágono corretamente. Além disso, respondemos à pergunta "o que é um hexágono?" usando a definição de simetria hexagonal.

Com a nossa calculadora de hexágonos, você pode explorar muitas propriedades geométricas e cálculos, inclusive como encontrar a área de um hexágono. Além do mais, você aprenderá como usar a calculadora para simplificar qualquer análise que envolva esse polígono de 6 lados.

Não é de se surpreender que o hexágono (também conhecido como "polígono de 6 lados") tenha exatamente seis lados. Esse fato é verdadeiro para todos os hexágonos, pois é a característica que os define. O comprimento dos lados pode variar, até mesmo dentro do mesmo hexágono, exceto quando se trata do hexágono regular, no qual todos os lados devem ter o mesmo comprimento.

Vamos nos aprofundar um pouco mais nesse polígono mais adiante, quando abordarmos conceitos sobre a área de um hexágono. Por enquanto, basta sabermos que o hexágono regular é o mais comum entre os polígonos de 6 lados e o mais frequentemente encontrado na natureza.

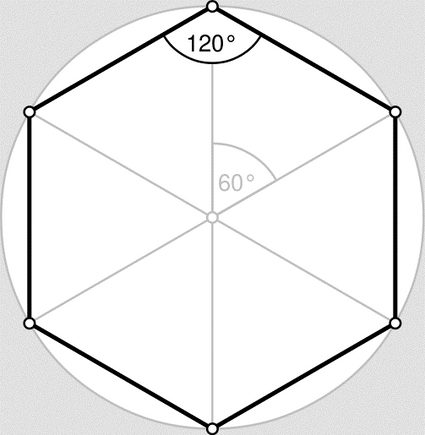
Haverá uma seção inteira dedicada às propriedades importantes do hexágono regular, mas, primeiro, precisamos saber a resposta técnica para: "O que é um hexágono?" Responder a essa pergunta nos ajudará a entender os truques que podemos usar para calcular a área de um hexágono sem usar cegamente a fórmula da área do hexágono. Esses truques envolvem o uso de outros polígonos, como quadrados, triângulos e até mesmo paralelogramos.

Como já mencionamos, o hexágono regular deve ter todos os lados com o mesmo comprimento e todos os seus ângulos internos devem ser iguais. Cada um dos lados possui o mesmo comprimento (o qual se repete em seus 6 lados!), portanto, calcular o perímetro de um hexágono é tão simples que você nem precisa da calculadora do perímetro de um polígono 🇺🇸. Basta calcular:

• perímetro = 6 × lado

Os ângulos de um hexágono arbitrário podem ter qualquer valor, mas todos eles devem somar 720º (você pode convertê-los facilmente em outras unidades usando nossa calculadora de conversão de ângulos 🇺🇸). Como o hexágono regular exige que todos os ângulos sejam iguais, logo cada ângulo individual deve ser de 120º. Veremos que esse fato é de extrema importância quando falamos sobre a popularidade do formato hexagonal na natureza. Ele também será útil quando explicarmos como encontrar a área de um hexágono regular. Também o usaremos para encontrar a fórmula da área dos hexágonos regulares.

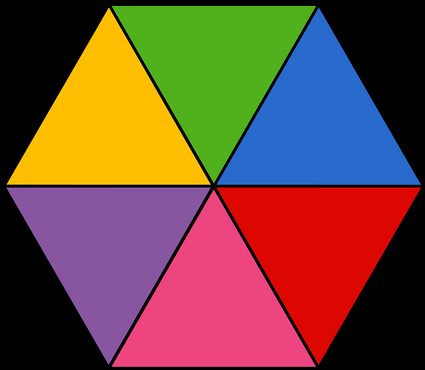
Agora, vamos dar uma olhada em como encontrar a área de um hexágono usando diferentes truques. A maneira mais fácil é usar nossa calculadora de hexágonos, que inclui uma ferramenta integrada de conversão de área. Para aqueles que querem saber como fazer isso manualmente, explicaremos como encontrar a área de um hexágono regular com e sem a fórmula da área do hexágono. A fórmula para a área de um polígono é sempre a mesma, independentemente de quantos lados ele tenha, desde que seja um polígono regular:

• área = apótema × perímetro / 2

Apenas para relembrar, o apótema é a distância entre o ponto médio de qualquer lado e o centro. Você pode visualizá-lo como a altura do triângulo equilátero formado por um lado e dois raios do hexágono (cada uma das áreas coloridas na imagem acima). Como alternativa, também é possível pensar no apótema como a distância entre o centro e qualquer lado do hexágono, já que a distância euclidiana é definida usando uma linha perpendicular.

Se não se lembrar da fórmula, você pode pensar no polígono de seis lados como um conjunto de seis triângulos. No caso do hexágono regular, esses triângulos são triângulos equiláteros, o que facilita muito o cálculo da sua área em comparação com triângulos isósceles ou até mesmo triângulos 45 45 90.

No caso do triângulo regular, todos os lados têm o mesmo comprimento, que é o comprimento do lado do hexágono que eles formam e que chamaremos de a. Já a altura de um triângulo será h = √3/2 ⋅ a, que é o valor exato do apótema nesse caso. Lembramos que √ significa raiz quadrada. Com isso, podemos começar com a matemática:

• A₀ = a ⋅ h / 2
• = a ⋅ √3/2 ⋅ a / 2
• = √3/4 ⋅ a²

onde A₀ significa a área de cada um dos triângulos equiláteros em que dividimos o hexágono. Após multiplicar essa área por seis (porque temos 6 triângulos), obtemos a fórmula da área do hexágono:

• A = 6 ⋅ A₀ = 6 ⋅ √3/4 ⋅ a²

• A = 3 ⋅ √3/2 ⋅ a²

• = (√3/2 ⋅ a) ⋅ (6 ⋅ a) /2

• = apótema × perímetro /2

Esperamos que agora seja mais fácil entender como obter a mesma fórmula de área de hexágono acima!

Se quiser ser mais criativo, você pode brincar com outras formas diferentes. Por exemplo, suponha que você divida o hexágono ao meio (de vértice a vértice). Nesse caso, você obtém dois trapézios e pode calcular a área do hexágono como a soma deles. Você também pode combinar dois triângulos adjacentes para construir um total de três losangos diferentes e calcular a área de cada um separadamente. Você pode até mesmo decompor o hexágono em um retângulo grande (usando as diagonais curtas) e dois triângulos isósceles!

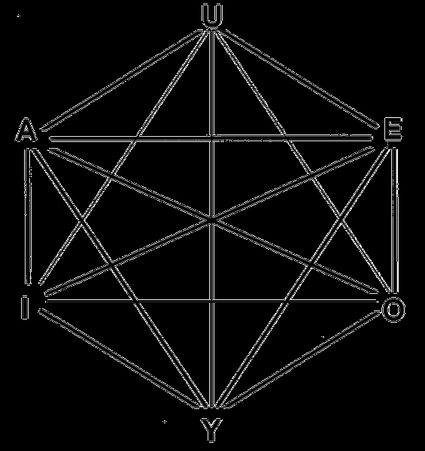
O número total de diagonais do hexágono é 9 - três delas são diagonais longas que cruzam o ponto central, e as outras seis são a chamadas de "altura" do hexágono.
Nossa calculadora de hexágono também pode poupá-lo de alguns cálculos tediosos sobre os comprimentos das diagonais do hexágono. Veja a seguir como calcular os dois tipos de diagonais:

• Diagonais longas - Sempre cruzam o ponto central do hexágono. Como você pode observar na figura acima, o comprimento dessa diagonal é igual ao comprimento de duas arestas:

  d = 2 ⋅ a

• Diagonais curtas - Nunca cruzam o ponto central. São construídas unindo dois vértices, deixando exatamente um entre eles. Seu comprimento é igual a:
  s = √3 ⋅ a

Outro par de valores importantes em um hexágono são o círculo circunscrito e o raio do círculo inscrito. O circunscrito é o raio da circunferência que contém todos os vértices do hexágono regular. O raio do círculo inscrito é o raio do maior círculo contido inteiramente dentro do hexágono.

• Circunscrito: para encontrar o raio de um círculo circunscrito no hexágono regular, você precisa determinar a distância entre o ponto central do hexágono (que também é o centro do círculo) e qualquer um dos vértices. Isso é simplesmente igual a R = a.

• Inscrito: o raio do círculo inscrito no hexágono regular é igual à metade da sua altura, que também é o apótema: r = √3/2 ⋅ a.

Agora vamos explorar um mundo mais prático e menos matemático: como desenhar um hexágono. Para um hexágono qualquer (irregular), a resposta é simples: desenhe qualquer forma de 6 lados, de modo que seja um polígono fechado, e é isso! Mas para um hexágono regular, as coisas não são tão fáceis, pois temos de garantir que todos os lados tenham o mesmo comprimento.

Para obter o resultado perfeito, você precisará de um compasso. Desenhe um círculo e, com o mesmo raio, comece a fazer marcas ao longo dele. Começando em um ponto aleatório e depois fazendo a próxima marca usando a anterior como ponto de ancoragem, desenhe um círculo com o compasso. Você terminará com 6 marcas e, quando uni-las com as linhas retas, terá um hexágono regular. Você pode ver um processo semelhante na animação acima.

A calculadora de hexágonos permite que você calcule vários parâmetros interessantes do polígono de 6 lados, que normalmente chamamos de hexágono. Usar essa calculadora é muito simples, com apenas um dos parâmetros você consegue calcular todos os outros. Além disso, a calculadora inclui uma ferramenta de conversão de comprimento integrada para cada um deles.

Discutimos todos os parâmetros da calculadora, mas, para fins de clareza e integridade, vamos examiná-los brevemente:

• Área - Superfície 2-D delimitada pela forma hexagonal;
• Comprimento Lateral - Distância de um vértice até o próximo vértice consecutivo;
• Perímetro - Soma dos comprimentos de todos os lados do hexágono;
• Diagonal longa - Distância de um vértice ao vértice oposto;
• Diagonal curta - Distância entre dois vértices, com outro vértice entre eles;
• Raio Circunscrito - Distância do centro a um vértice (igual ao raio do hexágono); e
• Raio Inscrito - O mesmo que o apótema.

Todo mundo adora uma boa aplicação no mundo real, não é mesmo? Os hexágonos são definitivamente um dos polígonos mais usados no mundo. Começando com os usos humanos, o mais fácil (e provavelmente menos empolgante) é o uso de hexágonos para pisos. O hexágono é uma forma excelente porque se encaixa perfeitamente um no outro para cobrir qualquer área desejada. Se estiver interessado nesse tipo de uso, recomendamos a calculadora de pisos e a calculadora de metragem quadrada 🇺🇸, pois são excelentes ferramentas para essa finalidade.

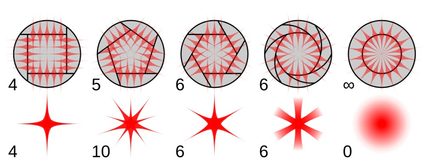
Esse caso é comum a todos os polígonos, mas ainda assim é interessante de se ver. Na fotografia, a abertura do sensor quase sempre tem uma forma poligonal. Essa parte da câmera é chamada de abertura e determina muitas propriedades e recursos das imagens produzidas por uma câmera. O mais inesperado é o formato de objetos muito brilhantes (semelhantes a pontos) devido ao efeito chamado grade de difração, ilustrado na figura acima.

Um dos usos mais valiosos dos hexágonos na era moderna, intimamente relacionado ao que falamos sobre fotografia, é na astronomia. Um dos maiores problemas que enfrentamos ao observar estrelas distantes é o fato de elas serem muito fracas no céu noturno. Isso ocorre porque, apesar de serem objetos muito brilhantes, elas estão tão distantes que apenas uma pequena fração de sua luz chega até nós; você pode saber mais sobre isso em nossa calculadora de luminosidade. Além disso, devido aos efeitos relativísticos (semelhantes à dilatação do tempo e à contração do comprimento), sua luz chega à Terra com menos energia do que foi emitida. Esse efeito é chamado de "desvio para o vermelho".

O resultado é que obtemos uma pequena quantidade de energia com um comprimento de onda maior do que gostaríamos. A melhor maneira de neutralizar isso é construir telescópios tão grandes quanto possível. O problema é que é quase impossível fabricar uma lente ou um espelho de peça única maior do que alguns metros, sem falar nos problemas de logística. A solução é construir um espelho modular usando ladrilhos hexagonais, como os que você pode ver nas fotos acima.

Fazer um espelho tão grande melhora a resolução angular do telescópio, bem como o fator de ampliação devido às propriedades geométricas de um "telescópio Cassegrain". Portanto, podemos dizer que, graças aos hexágonos regulares, podemos ver melhor, mais longe e com mais clareza do que jamais poderíamos ter visto com lentes ou espelhos de uma só peça.

Você sabia que as colchas hexagonais também existem? Descubra mais com a nossa calculadora de colcha hexagonal 🇺🇸!

O padrão de favo de mel é composto de hexágonos regulares dispostos lado a lado. Eles preenchem completamente toda a superfície que ocupam, de modo que não há buracos entre eles. Esse padrão de favo de mel aparece não apenas nos favos de mel (surpresa!), mas também em muitos outros lugares na natureza. Na verdade, ele é tão popular que se pode dizer que é a forma padrão quando não é possível utilizar círculos, por exemplo.

Das colmeias de abelhas às rachaduras nas rochas, passando pela química orgânica (até mesmo nos componentes básicos da vida, como nas proteínas), os hexágonos regulares são a forma poligonal mais comum que existe na natureza. E há uma razão para isso: os ângulos do hexágono. O ângulo de 120º é o mais estável mecanicamente de todos e, coincidentemente, é também o ângulo em que os lados se encontram nos vértices quando alinhamos hexágonos lado a lado. Para obter uma descrição completa da importância e das vantagens dos hexágonos regulares, recomendamos assistir este vídeo.

A maneira como os ângulos de 120º distribuem as forças (e, por sua vez, as tensões) entre 2 dos lados do hexágono, faz com que ele tenha uma geometria muito estável e mecanicamente eficiente. Essa é uma vantagem significativa dos hexágonos. Outra propriedade importante dos hexágonos regulares é que eles podem preencher uma superfície sem espaços entre eles (juntamente com os triângulos e quadrados regulares). Além disso, a forma regular de 6 lados tem o menor perímetro para a maior área entre os polígonos de preenchimento de superfície, o que a torna muito eficiente.

Um exemplo fascinante neste vídeo é o das bolhas de sabão. Quando você cria uma bolha usando água, sabão e ar, ela sempre tem um formato esférico. Esse resultado ocorre porque o volume de uma esfera é o maior de qualquer outro objeto para uma determinada área de superfície.

No entanto, quando colocamos as bolhas juntas em uma superfície plana, a esfera perde sua vantagem de eficiência, pois a seção de uma esfera não pode cobrir completamente um espaço 2D. O próximo melhor formato em termos de relação volume/área de superfície também é o melhor para equilibrar a tensão inter-bolhas criada na superfície das bolhas, ou seja, o nosso "todo-poderoso" hexágono.

As bolhas apresentam uma maneira interessante de visualizar os benefícios de um hexágono em relação a outras formas, mas não é a única maneira. Na natureza, como já mencionamos, há muitos exemplos de polígonos hexagonais, principalmente devido ao estresse e às tensões no material. Infelizmente, não podemos examinar todos eles em detalhes. Entretanto, podemos nomear alguns lugares onde é possível encontrar padrões hexagonais regulares na natureza:

• Favos de mel;
• Compostos orgânicos;
• Amontoado de bolhas;
• Formações rochosas (como a Calçada dos Gigantes);
• Olhos de insetos;
• ...