Calculadora da Diagonal de um Retângulo

A calculadora da diagonal de um retângulo da Omni é uma ferramenta abrangente que encontra rapidamente a diagonal e outros parâmetros de um retângulo. Você se deparou com algum problema específico do polígono retângulo ou ainda não sabe como encontrar a diagonal de um retângulo? Tente inserir alguns parâmetros nos campos ao lado do texto ou continue lendo para descobrir quais são as possíveis fórmulas da diagonal de um retângulo.

Você pode ver um retângulo típico na figura abaixo. Destacamos cinco parâmetros básicos que descrevem um retângulo específico. Você pode usá-los para derivar a fórmula da diagonal de um retângulo. São eles:

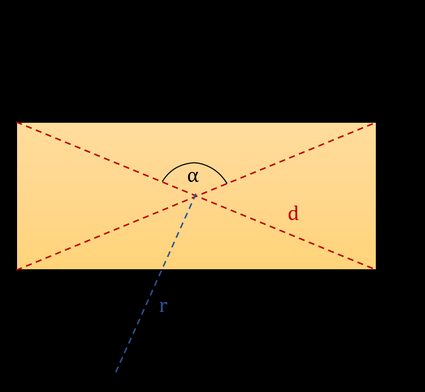
• l: comprimento;
• w: largura;
• α: o ângulo entre as diagonais;
• r: raio da circunferência;
• d: diagonal;

e dois outros parâmetros que não são mostrados na figura:

• A: área; e
• P: perímetro.

O termo retângulo vem do latim rectangulus, que é uma combinação de duas palavras: rectus (direito) e angulus (ângulo). Esse nome deriva do fato do retângulo ser um quadrilátero com quatro ângulos retos (4 ⋅ 90° = 360°). Seus lados opostos são paralelos e de igual comprimento, e suas duas diagonais se cruzam no meio e também são de igual comprimento.

Um quadrado é um caso especial de um retângulo. Sua definição é que ele tem todos os quatro lados de igual comprimento; alternativamente, o ângulo entre duas diagonais é reto. Experimente nossas calculadoras dedicadas a quadrados, por exemplo, a calculadora de quadrados 🇺🇸. Elas podem estimar rapidamente o perímetro, a área e a diagonal de qualquer quadrado que você quiser, apenas com o comprimento do seu lado.

O centro de um retângulo é equidistante de seus vértices; portanto, você pode sempre circunscrever um círculo nele. Por outro lado, você pode inscrever um círculo em um retângulo somente se ele for um quadrado.

Para determinar a diagonal de um retângulo, você precisa:

1. Anotar os lados do retângulo, que de acordo com nossa figura, denotamos por w e l.
2. Elevar ao quadrado esses dois valores. Ou seja, calcular l² e w².
3. Some os dois valores ao quadrado da Etapa 2.
4. Pegue a raiz quadrada do resultado.
5. É isso aí! Você acabou de encontrar o comprimento da diagonal do seu retângulo.

Por que esse procedimento funciona?

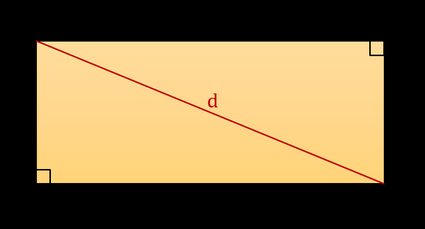
Para derivar a fórmula da diagonal de um retângulo usada acima, divida um retângulo em dois triângulos retângulos congruentes, ou seja, triângulos com um ângulo de 90°. Cada triângulo terá lados de comprimento l e w e uma hipotenusa de comprimento d. Você pode usar a fórmula da hipotenusa, por exemplo, ou usar a calculadora do Teorema de Pitágoras da Omni, para estimar a diagonal de um retângulo, que pode ser expressa com a seguinte fórmula:

d² = l² + w²

e agora você deve saber como encontrar a fórmula explícita da diagonal de um retângulo: basta tirar sua raiz quadrada:

d = √(l² + w²)

Nossa calculadora da diagonal de um retângulo permite que você use quase todas as unidades que desejar. Consulte os nossos conversor de comprimento ou conversor de área para saber como você pode alternar entre diferentes unidades.

Às vezes, não serão dados os comprimentos dos dois lados adjacentes de um retângulo. Como encontrar a diagonal de um retângulo nessa situação? A resposta é dada pela nossa calculadora de diagonal de um retângulo. Primeiro, vamos escrever três equações básicas para a área, o perímetro e o raio circunscrito:

1. Área de um retângulo: A = w ⋅ l,
2. Perímetro de um retângulo: P = 2 ⋅ w + 2 ⋅ l,
3. Raio circunscrito de um retângulo: r = d/2.

Com as equações acima, agora podemos derivar várias fórmulas da diagonal de um retângulo que são usadas nessa calculadora:

1. Dado comprimento e largura:
   d = √(l² + w²);

2. Dado comprimento/largura e área:

   d = √(A²/l² + l²) ou d = √(A²/w² + w²)

3. Dado comprimento/largura e perímetro:

   d = √(2l² − P ⋅ l + P²/4)) ou d = √(2w² − P ⋅ w + P²/4)

4. Dado comprimento/largura e ângulo:

   d = w / sen(α/2) ou d = l / cos(α/2)

5. Dada a área e o perímetro:

   d = ½√(P² - 8 ⋅ A)

6. Dada a área e o ângulo:

   d = √(2 ⋅ A / sen(α))

7. Dado perímetro e ângulo:

   d = P / (2 ⋅ sen(α/2) + 2 ⋅ cos(α/2))

8. Dado o raio do círculo:

   d = 2 ⋅ r

Observação: O ângulo α entre as diagonais é oposto ao comprimento l, como na primeira figura. Além disso, lembre-se de que a calculadora da diagonal de um retângulo pressupõe que o comprimento seja maior que a largura!

Você sabia que existe um retângulo especial chamado retângulo de ouro? Se não, vá para a nossa calculadora do retângulo de ouro para saber como você pode construir retângulos de ouro, ou retângulos áureos!