Calculadora de Triângulos Semelhantes

A calculadora de triângulos semelhantes da Omni te ajuda a encontrar um triângulo semelhante ao redimensionar um triângulo conhecido. Você também pode usar esta calculadora para encontrar o comprimento ausente de um triângulo semelhante a outro!

Se você quiser, continue lendo este artigo, pois discutiremos as leis de semelhança de triângulos e aprenderemos alguns fundamentos:

• O que são triângulos semelhantes?
• Como encontrar triângulos semelhantes?
• Como determinar se dois triângulos são semelhantes?
• Como encontrar o lado ausente de um triângulo semelhante?
• Como encontrar a área de um triângulo semelhante?

Dois triângulos são semelhantes se seus lados correspondentes estiverem na mesma proporção, o que significa que um triângulo é uma versão escalonada do outro. Naturalmente, os ângulos correspondentes dos triângulos semelhantes são iguais. Por exemplo, considere os dois triângulos a seguir:

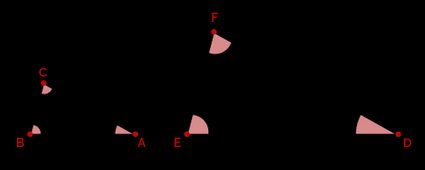
Observe que os lados correspondentes estão em proporção:

Portanto, podemos dizer que $\triangle \text{ABC}$ $\sim$ $\triangle \text{DEF}$ . Aqui o símbolo $\sim$ indica que os triângulos são semelhantes.

Denominamos a proporção de semelhança como fator de escala $(k)$. No exemplo acima, o fator de escala é $k = 2$. Se você precisar de ajuda para encontrar proporções, use a calculadora de proporções da Omni.

Você sabe que dois triângulos são semelhantes se uma das seguintes opções for verdadeira:

• Os lados correspondentes do triângulo estão em proporção; ou
• Os ângulos correspondentes são iguais.

A partir disso, podemos derivar regras específicas para determinar se dois triângulos são semelhantes:

1. Lado-Lado-Lado (LLL): Se todos os três lados correspondentes dos dois triângulos estiverem em proporção, eles são semelhantes. Essa regra é a mais direta e é necessário que você conheça todos os lados dos triângulos.

Você pode expressar isso usando uma fórmula de triângulos similar:

onde $k$ é o fator de escala.

2. Lado-Angulo-Lado (LAL): Se quaisquer dois lados correspondentes de dois triângulos estiverem em proporção e seus ângulos internos forem iguais, então os triângulos são semelhantes. Você pode usar essa regra sempre que conhecer apenas dois lados de cada triângulo, incluindo seus ângulos.

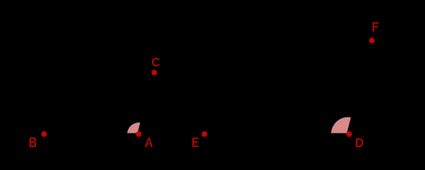
Os triângulos na imagem acima são semelhantes se:

Essa regra é útil em casos como o da imagem abaixo, em que os triângulos compartilham um ângulo:

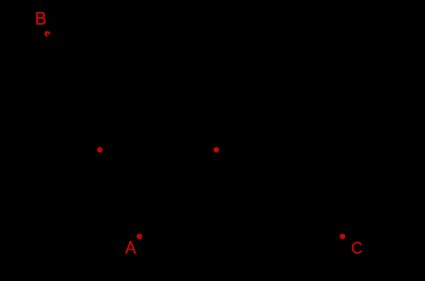
Você pode fazer muitas coisas conhecendo apenas dois lados e um ângulo de um triângulo. Saiba mais usando a calculadora de triângulos LAL 🇺🇸.

3. Ângulo-Lado-Ângulo (ALA): Se quaisquer dois ângulos correspondentes de dois triângulos forem iguais e os lados correspondentes entre eles estiverem em proporção, os triângulos são semelhantes.

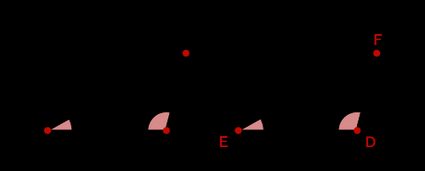
Os triângulos na imagem acima são semelhantes se:

Você pode encontrar o terceiro ângulo se souber quaisquer dois ângulos em um triângulo usando nossa calculadora de ângulos de um triângulo. Sabemos que, se quaisquer dois ângulos correspondentes nos triângulos forem iguais, os triângulos são semelhantes. Isso significa que, na regra de congruência ALA, não precisamos saber o lado, desde que os ângulos sejam conhecidos. No entanto, sem os lados, não podemos determinar o fator de escala $k$.

Para encontrar o lado ausente de um triângulo usando o lado correspondente de um triângulo semelhante, siga os passos a seguir:

1. Encontre o fator de escala k dos triângulos semelhantes pegando a razão de qualquer lado conhecido no triângulo maior e seu lado correspondente no triângulo menor.
2. Determine se o triângulo com o lado ausente é menor ou maior.
3. Se o triângulo for menor, divida seu lado correspondente no triângulo maior por k para obter o lado ausente. Caso contrário, você deve multiplicar o lado correspondente no triângulo menor por k para encontrar o lado ausente.

Por exemplo, considere os dois triângulos semelhantes a seguir.

Para encontrar o lado ausente, primeiro começamos calculando seu fator de escala.

Em seguida, usamos a relação do fator de escala entre o lado ausente AC e seu lado correspondente DF:

Para encontrar a área de um triângulo A1 a partir da área de seu triângulo semelhante A2, siga os passos a seguir:

1. Encontre o fator de escala k dos triângulos semelhantes pegando a razão de qualquer lado conhecido no triângulo maior e seu lado correspondente no triângulo menor.
2. Determine se o triângulo com a área desconhecida é menor ou maior.
3. Se o triângulo for menor, divida A2 pelo quadrado do fator de escala k para obter A1 = A2/k². Caso contrário, você deve multiplicar A2 por k² para obter A1 = A2 ⋅ k².

Agora que você já aprendeu a descobrir o comprimento de um triângulo semelhante, a fórmula de triângulos semelhantes e muito mais, pode descobrir rapidamente como funciona esta calculadora de triângulos semelhantes.

Para verificar se dois triângulos conhecidos são semelhantes, você pode usar esta calculadora da seguinte forma:

1. Selecione verificar semelhança no campo Tipo.
2. Escolha o critério de semelhança que você deseja usar. Você pode escolher entre Lado-Lado-Lado, Lado-Ângulo-Lado e Ângulo-Lado-Ângulo.
3. Digite as dimensões dos dois triângulos. A calculadora avaliará se eles são semelhantes ou não.

Para resolver o lado ou o perímetro de semelhanças de triângulos, siga os passos a seguir:

1. Selecione encontrar o lado ausente no campo Tipo.
2. Insira as dimensões conhecidas, a área, o perímetro e o fator de escala dos triângulos. A calculadora de semelhança de triângulos encontrará os valores desconhecidos.

Sim, se os ângulos correspondentes de dois triângulos forem iguais, os triângulos são semelhantes. Como todos os ângulos de um triângulo equilátero são iguais a 60°, todos os triângulos equiláteros são semelhantes.

O fator de escala é 1,414. Para determinar esse fator de escala baseado em duas áreas, siga os passos a seguir:

1. Divida a área maior pela área menor para obter 20/10 = 2.
2. Encontre a raiz quadrada desse valor para obter o fator de escala, k = √2 = 1,414.
3. Verifique esse resultado usando a calculadora de triângulos semelhantes da Omni.