Calculadora de Raiz Quadrada

A calculadora de raiz quadrada da Omni irá calcular raiz quadrada de qualquer número positivo que você desejar. Basta você digitar o número escolhido e ler os resultados. Com essa ferramenta você calculará qual a raiz quadrada de 2 e de vários outros números de forma rápida e automática. Você também pode estimar o quadrado do número desejado (basta digitar o valor no segundo campo), o que pode ser de grande ajuda para encontrar quadrados perfeitos a partir da fórmula da raiz quadrada.

Você tem dificuldades com as operações aritméticas básicas: adição, subtração, multiplicação ou divisão de raízes quadradas? Agora você não tem mais! No texto a seguir, você encontrará uma explicação detalhada sobre as diferentes propriedades da raiz quadrada, por exemplo, como simplificar raízes quadradas, com vários exemplos apresentados. Com este artigo, você aprenderá de uma vez por todas como encontrar raízes quadradas!

Você já se perguntou qual é a origem do símbolo da raiz quadrada √? Podemos garantir que essa história não é tão simples como você pode pensar a princípio. A origem do símbolo da raiz quadrada remonta aos tempos antigos, como a origem da porcentagem.

Se você estiver procurando o gráfico da raiz quadrada ou as propriedades da função da raiz quadrada, vá diretamente para a seção apropriada (basta clicar nos links acima!). Lá, explicamos o que é a derivada de uma raiz quadrada usando uma definição fundamental de raiz quadrada; também explicamos como calcular raiz quadrada de expoentes ou de frações. Por fim, se você for persistente o suficiente nessa leitura, descobrirá que a raiz quadrada de número negativo é, de fato, possível. Dessa forma, apresentamos os números complexos, que encontram amplas aplicações na física e na matemática.

A operação da raiz quadrada de um número já era conhecida na antiguidade. A mais antiga tábua de argila com o valor correto de até 5 casas decimais de √2 = 1,41421 vem da Babilônia (1800 A.E.C. - 1600 A.E.C.). Muitos outros documentos mostram que as raízes quadradas também eram usadas pelos antigos egípcios, indianos, gregos e chineses. Entretanto, a origem do símbolo da raiz quadrada √ ainda é amplamente especulativa.

• Muitos estudiosos acreditam que as raízes quadradas se originam da letra "r ": a primeira letra da palavra latina radix, que significa raiz.
• Outra teoria afirma que o símbolo da raiz quadrada foi tirado da letra árabe ج que foi colocada em sua forma original de ﺟ na palavra جذر - raiz (o idioma árabe é escrito da direita para a esquerda).

O primeiro uso do símbolo da raiz quadrada √ não incluía a "barra" horizontal sobre os números dentro do símbolo da raiz quadrada (ou radical), √‾. A "barra" é conhecida como vinculum em latim, que significa ligação. Embora o símbolo de radical com vinculum seja agora de uso cotidiano, geralmente omitimos esse sublinhado em muitos textos, como em artigos na Internet. A notação dos graus mais altos de uma raiz foi sugerida por Albert Girard, que colocou o índice de grau dentro da abertura do sinal de radical, por exemplo, ³√ ou ⁴√.

A última pergunta é: por que a operação de raiz quadrada é chamada de raiz, independentemente de sua verdadeira origem? A explicação se tornará mais evidente se escrevermos a equação x = ⁿ√a em uma forma diferente: xⁿ = a. x é chamado de raiz ou radical porque é a base oculta de a. Assim, a palavra radical não significa alcance distante ou extremo, mas sim fundamental, atingindo a causa raiz.

Até agora você já ficou sabendo muitos fatos interessantes sobre raízes quadradas, mas o que é raiz quadrada? Na matemática, as operações tradicionais com números são adição, subtração, multiplicação e divisão. No entanto, às vezes adicionamos a essa lista algumas operações e manipulações mais avançadas: raízes quadradas, expoentes, logaritmos e até mesmo funções trigonométricas (por exemplo, seno e cosseno). Neste artigo, vamos nos concentrar apenas em o que é raiz quadrada.

A raiz quadrada de um determinado número x é todo número y cujo quadrado y² = y · y resulta no número original x. Portanto, a fórmula da raiz quadrada pode ser expressa como:

√x = y ⟺ x = y²,

onde ⟺ é um símbolo matemático que significa se e somente se. Cada número real positivo sempre tem duas raízes quadradas, a primeira é positiva e a segunda é negativa. Entretanto, para muitos fins práticos, geralmente usamos a positiva. O único número que tem uma raiz quadrada é o zero. Isso ocorre porque √0 = 0, e zero não é positivo nem negativo.

Há também outra notação comum de raízes quadradas que pode ser mais conveniente em muitos cálculos complexos. Essa fórmula alternativa de raiz quadrada afirma que a raiz quadrada de um número é um número elevado ao expoente da fração pela metade:

√x = x^(1/2) = x^0,5

Na interpretação geométrica, a raiz quadrada de uma determinada área de um quadrado fornece o comprimento de seu lado. É por isso que √ tem a palavra quadrado em seu nome. Uma situação semelhante ocorre com a raiz cúbica, ∛. Se você tirar a raiz cúbica do volume de um cubo, obterá o comprimento de suas arestas. Enquanto as raízes quadradas são usadas ao considerar as áreas de superfície, as raízes cúbicas são úteis para determinar quantidades relacionadas ao volume, por exemplo, a densidade.

Talvez não estejamos sendo muito modestos, mas achamos que a melhor resposta para a pergunta sobre como resolver raiz quadrada é simples: usando a nossa calculadora de raiz quadrada! Você pode usá-la tanto no computador quanto no smartphone para estimar rapidamente a raiz quadrada de um determinado número. Infelizmente, às vezes há situações em que você precisa calcular e confiar apenas em si mesmo. E então? Para se preparar para isso, você deve se lembrar de várias raízes quadradas perfeitas básicas:

• Raiz quadrada de 1: √1 = 1, já que 1 · 1 = 1;
• Raiz quadrada de 4: √4 = 2, já que 2 · 2 = 4;
• Raiz quadrada de 9: √9 = 3, já que 3 · 3 = 9;
• Raiz quadrada de 16: √16 = 4, pois 4 · 4 = 16;
• Raiz quadrada de 25: √25 = 5, pois 5 · 5 = 25;
• Raiz quadrada de 36: √36 = 6, pois 6 · 6 = 36;
• Raiz quadrada de 49: √49 = 7, pois 7 · 7 = 49;
• Raiz quadrada de 64: √64 = 8, já que 8 · 8 = 64;
• Raiz quadrada de 81: √81 = 9, já que 9 · 9 = 81;
• Raiz quadrada de 100: √100 = 10, já que 10 · 10 = 100;
• Raiz quadrada de 121: √121 = 11, pois 11 · 11 = 121; e
• Raiz quadrada de 144: √144 = 12, pois 12 · 12 = 144.

A raiz quadrada de 1 e a raiz quadrada de 9 são as raízes quadradas mais simples. A lista acima também é fácil de lembrar, pois ao calcular a raiz você sempre obtém um número inteiro. Tente se lembrar deles! O que você pode fazer quando há um número que não tem uma raiz quadrada inteira? Qual a raiz quadrada de 2? E a raiz quadrada de 8? Calma! Iremos te explicar como encontrá-las com algumas soluções. Em primeiro lugar, você pode tentar prever o resultado por tentativa e erro. Digamos que você queira estimar a raiz quadrada de 52:

1. Você sabe que √49 = 7 e √64 = 8, portanto √52 deve estar entre 7 e 8.

2. O número 52 está mais próximo de 49 (efetivamente mais próximo de 7), então você pode tentar adivinhar que √52 é 7,3.

3. Em seguida, você eleva 7,3 ao quadrado, obtendo 7,3² = 53,29 (como diz a fórmula da raiz quadrada), que é maior que 52. Você precisa tentar com um número menor, digamos 7,2.

4. O quadrado de 7,2 é 51,84. Agora você tem um número menor, mas muito mais próximo de 52. Se essa precisão o satisfaz, você pode encerrar as estimativas aqui. Caso contrário, você pode repetir o procedimento com um número escolhido entre 7,2 e 7,3, por exemplo, 7,22, e assim por diante.

Outra abordagem é simplificar a raiz quadrada primeiro e depois usar as aproximações das raízes quadradas dos números primos (normalmente arredondadas para duas casas decimais):

• Raiz quadrada de 2: √2 ≈ 1,41,
• Raiz quadrada de 3: √3 ≈ 1,73,
• Raiz quadrada de 5: √5 ≈ 2,24,
• Raiz quadrada de 7: √7 ≈ 2,65,
• Raiz quadrada de 8: √8 ≈ 2,83,
• Raiz quadrada de 11: √11 ≈ 3,32,
• Raiz quadrada de 13: √13 ≈ 3,61,
• Raiz quadrada de 17: √17 ≈ 4,12,
• Raiz quadrada de 19: √19 ≈ 4,34, etc.

Vamos tentar encontrar a raiz quadrada de 52 novamente. Você pode simplificá-la para √52 = 2√13 (você aprenderá como simplificar a raiz quadrada na próxima seção) e, em seguida, substituir √13 ≈ 3,61. Por fim, faça uma multiplicação √52 ≈ 2 · 3,61 = 7,22. O resultado é o mesmo que o anterior! Confira o resultado na nossa calculadora de raiz quadrada!

Em algumas situações, você não precisa saber o resultado exato da raiz quadrada. Se esse for o caso, nossa calculadora de raiz quadrada é a melhor opção para estimar o valor de toda raiz quadrada que você desejar. Por exemplo, digamos que você queira saber se 4√5 é maior que 9. Pela calculadora, você sabe que √5 ≈ 2,23607, portanto 4√5 ≈ 4 · 2,23607 = 8,94428. Esse valor está muito próximo do 9, mas não é maior que ele! A calculadora de raiz quadrada fornece o valor final com precisão relativamente alta (até cinco dígitos no exemplo acima).

Lembre-se de que nossa calculadora recalcula automaticamente os números inseridos em qualquer um dos campos. Você pode encontrar a raiz quadrada de um número específico preenchendo o primeiro campo ou obtendo o quadrado de um número que você inseriu no segundo campo. A segunda opção é útil para encontrar quadrados perfeitos, que são essenciais em muitos aspectos da matemática e da ciência. Por exemplo, se você inserir 17 no segundo campo, descobrirá que 289 é um quadrado perfeito.

Em algumas aplicações da raiz quadrada, especialmente aquelas relacionadas a ciências como química e física, os resultados são preferidos em notação científica. Em resumo, uma resposta em notação científica deve ter um ponto decimal entre os dois primeiros números diferentes de zero. Ela será representada como o decimal multiplicado por 10 elevado a um expoente. Por exemplo, o número 0,00345 é escrito como 3,45 × 10⁻³ em notação científica, enquanto 145,67 é escrito como 1,4567 × 10² em notação científica. Os resultados obtidos usando a calculadora de raiz quadrada podem ser convertidos em notação científica com a calculadora de notação científica.

Primeiro, vamos nos perguntar quais raízes quadradas podem ser simplificadas. Para responder a essa pergunta, você precisa pegar o número que está após o símbolo da raiz quadrada e encontrar seus fatores. Se algum de seus fatores for um número quadrado perfeito (1, 4, 9, 16, 25, 36, 49, 64 e assim por diante), você poderá simplificar a raiz quadrada. Por que esses números são chamados quadrados perfeitos? Eles podem ser expressos respectivamente como 2², 3², 4², 5², 6², 7² e assim por diante. De acordo com a definição de raiz quadrada, você pode chamá-los de quadrados perfeitos. Vamos dar uma olhada em alguns exemplos:

• Você pode simplificar √27? Os fatores de 27 são: 1, 3, 9, 27. Isso significa que você pode simplificar √27.

• Você pode simplificar √15? Os fatores de 15 são 1, 3, 5 e 15. Não há quadrados perfeitos nesses números, portanto, essa raiz quadrada não pode ser simplificada.

Então, como simplificar raízes quadradas? Para explicar isso, usaremos uma propriedade útil da raiz quadrada sobre a qual falamos anteriormente, ou seja, a fórmula alternativa da raiz quadrada:

√x = x^(1/2)

Podemos usar essas duas formas de raiz quadrada e alternar entre elas sempre que quisermos. Em particular, lembramos que a potência da multiplicação de dois números específicos é equivalente à multiplicação desses números específicos elevados às mesmas potências. Portanto, podemos escrever:

(x · y)^(1/2) = x^(1/2) · y^(1/2) ⟺ √(x · y) = √x · √y,

Como você pode usar esse conhecimento? O argumento de uma raiz quadrada geralmente não é um quadrado perfeito que você possa calcular facilmente, mas pode conter um quadrado perfeito entre seus fatores. Em outras palavras, você pode escrevê-lo como uma multiplicação de dois números, em que um dos números é o quadrado perfeito, por exemplo, 45 = 9 × 5 (9 é um quadrado perfeito). A exigência de que você tenha pelo menos um fator que seja um quadrado perfeito é necessária para simplificar a raiz quadrada. A essa altura, você provavelmente já deve saber qual será a próxima etapa. Você precisa colocar essa multiplicação sob a raiz quadrada. Em nosso exemplo:

√45 = 45^(1/2) = (9 · 5)^(1/2) = 9^(1/2) × 5^(1/2) = √9 · √5 = 3√5.

Você aprendeu com sucesso a simplificar a sua primeira raiz quadrada! É claro que você não precisa escrever todos esses cálculos. Desde que se lembre de que raiz quadrada é equivalente à potência de um meio, você pode simplificá-los. Vamos praticar a simplificação de raízes quadradas com alguns outros exemplos:

• Como simplificar a raiz quadrada de 27?

  √27 = √(9 · 3) = √9 · √3 = 3√3

• Como simplificar a raiz quadrada de 8?

  √8 = √(4 · 2) = √4 · √2 = 2√2

• Como simplificar a raiz quadrada de 144?

  √144 = √(4 · 36) = √4 · √36 = 2 · 6 = 12

No último exemplo, você não precisava simplificar a raiz quadrada porque 144 é um quadrado perfeito. Você poderia simplesmente lembrar que 12 · 12 = 144. No entanto, queríamos mostrar que, com o processo de simplificação, você também pode calcular facilmente as raízes quadradas de quadrados perfeitos. Isso é útil quando você lida com números grandes.

Por fim, você pode perguntar como simplificar raízes de ordens superiores, por exemplo, raízes cúbicas. Você pode ver mais detalhes na calculadora de raiz cúbica. Mas, na verdade, o processo é análogo ao das raízes quadradas, só que no caso das raízes cúbicas, você precisa encontrar pelo menos um fator que seja um cubo perfeito, não um quadrado perfeito, ou seja, 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ e assim por diante. Em seguida, você divide o número em duas partes e as coloca sob a raiz cúbica. Vejamos o seguinte exemplo de simplificação de ³√192:

∛192 = ∛(64 · 3) = ∛64 · ∛3 = 4∛3

Pode parecer um pouco complicado à primeira vista, mas depois de alguma prática, você será capaz de simplificar as raízes na sua cabeça. Mas lembre-se que você sempre pode recorrer ao uso de uma calculadora de raiz quadrada online!

Somando e subtraindo raízes quadradas

Infelizmente, somar ou subtrair raízes quadradas não é tão fácil quanto somar/subtrair números regulares. Por exemplo, se 2 + 3 = 5, isso não significa que √2 + √3 é igual a √5. Para entender por que isso acontece, imagine que você tenha dois tipos diferentes de formas: triângulos 🔺 e círculos 🔵. O que acontece quando você soma um triângulo com um círculo 🔺 + 🔵? Nada! Você ainda tem um triângulo e um círculo 🔺 + 🔵. Por outro lado, o que acontece quando você tenta somar três triângulos com cinco triângulos? 3🔺 + 5🔺? Você terminará com oito triângulos 8🔺.

A adição de raízes quadradas é muito semelhante a isso. O resultado da adição de √2 + √3 ainda é √2 + √3. Você não pode simplificá-lo ainda mais. No entanto, a situação é diferente quando ambas as raízes quadradas têm o mesmo número sob o símbolo da raiz quadrada. Então, você pode adicioná-las como se fossem números regulares (ou triângulos). Por exemplo, 3√2 + 5√2 é igual a 8√2. O mesmo se aplica à subtração de raízes quadradas. Vamos dar uma olhada em mais exemplos que ilustram essa propriedade da raiz quadrada:

• Quanto é 6√17 + 5√17? Resposta: 6√17 + 5√17 = 11√17;

• Quanto é 4√7 - 7√7? Resposta: 4√7 - 7√7 = -3√7;

• Quanto é 2√2 + 3√8? Resposta: 2√2 + 3√8 = 2√2 + 6√2 = 8√2, porque simplificamos √8 = √(4 · 2) = √4 · √2 = 2√2;

• Quanto é √45 - √20? Resposta: √45 - √20 = 3√5 - 2√5 = √5, porque simplificamos √45 = √(9 · 5) = √9 · √5 = 3√5 e √20 = √(4 · 5) = √4 · √5 = 2√5;

• Quanto é 7√13 + 2√22? Resposta: 7√13 + 2√22, não é possível simplificar mais;

• Quanto é √3 - √18? Resposta: √3 - √18 = √3 - 3√2, não podemos simplificar mais do que isso, mas pelo menos simplificamos √18 = √(9 · 2) = √9 · √2 = 3√2.

Multiplicação de raízes quadradas e divisão de raízes quadradas

Agora que a adição de raízes quadradas é muito fácil para você, vamos dar um passo adiante. O que você acha de multiplicar e dividir raízes quadradas? Não se assuste! Na verdade, você já fez isso durante a lição sobre simplificação de raízes quadradas. A multiplicação de raízes quadradas se baseia na propriedade da raiz quadrada que já usamos algumas vezes, ou seja:

√x = x^(1/2)

Você se lembra de como multiplicar números que são elevados à mesma potência? Para relembrar:

xⁿ · yⁿ = (x · y)ⁿ,

e, portanto

x^(1/2) · y^(1/2) = (x · y)^(1/2) ⟺ √x · √y = √(x · y).

Ao contrário da adição, você pode multiplicar cada duas raízes quadradas. Lembre-se de que a multiplicação tem propriedades comutativas, o que significa que a ordem em que dois números são multiplicados não importa. Alguns exemplos devem esclarecer essa questão:

• Quanto é √3 · √2? Resposta: √3 · √2 = √6;

• Quanto é 2√5 · 5√3? Resposta: 2√5 · 5√3 = 2 · 5 · √5 · √3 = 10√15, porque a multiplicação é comutativa;

• Quanto é 2√6 · 3√3? Resposta: 2√6 · 3√3 = 2 · 3 · √6 · √3 = 6√18 = 18√2, simplificamos √18 = √(9 · 2) = √9 · √2 = 3√2.

Dividir uma raiz quadrada é quase a mesma coisa, pois:

x^(1/2) / y^(1/2) = (x / y)^(1/2) ⟺ √x / √y = √(x / y).

Tudo o que você precisa fazer é substituir o sinal de multiplicação pelo de divisão. No entanto, a divisão não é um operador comutativo! Você precisa calcular os números que estão antes das raízes quadradas e os números abaixo das raízes quadradas separadamente. Como sempre, aqui estão alguns exemplos práticos:

• Quanto é √15 / √3? Resposta: √15 / √3 = √5;

• Quanto é 10√6 / 5√2? Resposta: 10√6 / 5√2 = (10 / 5) · (√6 / √2) = 2√3;

• Quanto é 6√2 / 3√5? Resposta: 6√2 / 3√5 = (6 / 3) · (√2 / √5) = 2√(2/5) = 2√(0,4), trocamos a fração simples 2/5 pela fração decimal 2/5 = 4/10 = 0,4.

Calcular a raiz quadrada do expoente ou a raiz quadrada da fração pode não estar claro para você. Mas com o conhecimento que adquiriu na seção anterior, você deve achar mais fácil do que esperava! Vamos começar com as raízes quadradas de potências. Nesse caso, será mais fácil para você usar a forma alternativa de raiz quadrada √x = x^(1/2). Você se lembra da regra da potência? Se não, aqui está um lembrete rápido:

(xⁿ)^m = x^{(n · m)},

onde n e m são números reais quaisquer. Agora, quando você colocar 1/2 em vez de m, obterá apenas uma raiz quadrada:

√(xⁿ) = (xⁿ)^(1/2) = x^(n/2),

e é assim que você encontra a raiz quadrada de um expoente. Por falar em potências, a equação acima é muito semelhante à função densidade de probabilidade, que é amplamente usada em estatística.

Se você ainda não tem certeza sobre a obtenção de raízes quadradas de potências, aqui estão alguns exemplos:

• Raiz quadrada de 2⁴: √(2⁴) = (2⁴)^(1/2) = 2^(4/2) = 2² = 4;
• Raiz quadrada de 5³: √(5³) = (5³)^(1/2) = 5^(3/2); e
• Raiz quadrada de 4⁵: √(4⁵) = (4⁵)^(1/2) = 4^(5/2) = (2²)^(5/2) = 2⁵ = 32.

Como você pode ver, às vezes é impossível obter um resultado exato como o do primeiro exemplo. Entretanto, no terceiro exemplo, mostramos a você um pequeno truque para expressar 4 como 2². Com essa abordagem, você pode simplificar equações mais complicadas.

E quanto às raízes quadradas de frações? Dê uma olhada na seção anterior, onde escrevemos sobre a divisão de raízes quadradas. Você pode encontrar lá a seguinte relação que deve explicar tudo:

(x / y)^(1/2) ⟺ √x / √y = √(x / y),

em que x / y é uma fração. Abaixo você pode encontrar alguns exemplos de raízes quadradas de uma fração:

• Raiz quadrada de 4/9: √(4/9) = √4 / √9 = 2/3;
• Raiz quadrada de 1/100: √(1/100) = √1 / √100 = 1/10; e
• Raiz quadrada de 1/5: √(1/5) = √1 / √5 = 1/√5 = √5/5.

Deixar raízes no denominador não é indicado. É por isso que nos livramos dele no último exemplo. Apenas multiplicamos o numerador e o denominador pelo mesmo número (sempre podemos fazer isso, pois o número pelo qual multiplicamos é igual a 1), nesse caso, por √5.

As funções desempenham um papel fundamental não apenas na matemática, mas em muitas outras áreas, como física, estatística ou finanças. A função f(x) nada mais é do que uma fórmula que diz como o valor de f(x) muda com o argumento x. Você encontrará algumas funções que podem ser aplicadas na vida real. Elas são de grande ajuda se você quiser saber como calcular juros compostos ou estimar o valor futuro de uma anuidade.

Abaixo, você pode encontrar o gráfico da raiz quadrada, composto pela metade de uma parábola. Verifique-o e tente validar, por exemplo, se a função da raiz quadrada de x = 9 é 3 e de x = 16 é 4 (como deveria ser).

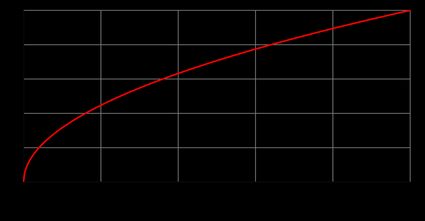
Vamos voltar à função de uma raiz quadrada, a qual chamamos de função irracional, f(x) = √x, e explorar quais são suas propriedades básicas. Consideramos aqui apenas a parte positiva de f(x) (como você pode ver no gráfico de raiz quadrada acima). Portanto, a função raiz quadrada:

• É contínua e crescente para todo x não negativo;

• É diferenciável para todos os x positivos (consulte a seção "derivada da raiz quadrada" (logo abaixo) para obter mais informações;

• Aproxima-se do limite do infinito à medida que x se aproxima do infinito (lim √x → ∞ quando x → ∞); e

• É um número real para todo x não negativo e um número complexo para todo x negativo.

A derivada de uma função nos informa a velocidade com que essa função muda com seu argumento. Um dos exemplos mais simples em física é a posição de um objeto e sua velocidade (a taxa de mudança de posição). Digamos que a função x(t) descreva como a distância do carro em movimento de um ponto específico muda com o tempo t. Você sabe o que determina a rapidez da mudança na distância percorrida? A resposta é a velocidade do carro! Portanto, a derivada da posição x(t) é a velocidade v(t) (a velocidade também pode depender do tempo). Para denotar a derivada, geralmente usamos o apóstrofo v(t) = x'(t) ou o símbolo de derivada v(t) = dx(t)/dt.

A derivada da função geral f(x) nem sempre é fácil de calcular. Entretanto, em algumas circunstâncias, se a função assumir uma forma específica, você terá algumas fórmulas. Por exemplo, se

f(x) = xⁿ,

onde n é qualquer número real, a derivada é a seguinte:

f'(x) = n · x^(n-1).

Talvez não pareça, mas isso responde à pergunta qual é a derivada de uma raiz quadrada. Você se lembra da forma alternativa (exponencial) de uma raiz quadrada? Vamos lembrar você:

√x = x^(1/2).

Você pode ver que, nesse caso, n = 1/2, portanto, a derivada de uma raiz quadrada é:

(√x)' = (x^(1/2))' = 1/2 · x^(-1/2) = 1/(2√x).

Como um número elevado a uma potência negativa é um sobre esse número, a estimativa da derivação envolverá frações. Temos uma ferramenta que pode ser essencial ao adicionar ou subtrair frações com denominadores diferentes: a calculadora de MMC, que diz a você como encontrar o Mínimo Múltiplo Comum.

A derivada de uma raiz quadrada é necessária para que você obtenha os coeficientes na chamada expansão de Taylor. Não queremos entrar em detalhes muito profundos, então, resumidamente, a série de Taylor permite que você aproxime várias funções a partir de uma combinação de polinômios, que são muito mais fáceis de calcular. Por exemplo, a expansão de Taylor de √(1 + x) sobre o ponto x = 0 é dada por:

√(1 + x) = 1 + 1/2 · x - 1/8 · x² + 1/16 · x³ - 5/128 · x⁴ + ...,

que é válido para -1 ≤ x ≤ 1. Embora a expressão acima tenha um número infinito de termos, para obter o valor aproximado, você pode usar apenas alguns dos primeiros termos. Vamos tentar! Com x = 0,5 e os primeiros cinco termos, você obtém:

√(1,5) = 1 + 1/2 · 0,5 - 1/8 · 0,25 + 1/16 · 0,125 - 5/128 · 0,0625,

√(1,5) ≈ 1,2241,

e o valor real, fornecido pela nossa calculadora, é √(1,5) ≈ 1,2247. Está bem próximo!

Até agora, você já fez muitas contas e equações. Para você que é persistente o suficiente, preparamos a próxima seção, que explica como calcular raiz quadrada de número negativo.

Na escola, você provavelmente aprendeu que a raiz quadrada de número negativo não existe. Isso é verdade quando você considera apenas os números reais. Há muito tempo, para realizar cálculos avançados, os matemáticos tiveram que introduzir um conjunto mais geral de números: os números complexos. Eles podem ser expressos da seguinte forma:

x = a + b · i,

onde x é o número complexo com a parte real a e a parte imaginária b. A diferença entre um número complexo e um real é o número imaginário i. Aqui você tem alguns exemplos de números complexos: 2 + 3i, 5i, 1,5 + 4i e 2. Você pode se surpreender ao ver 2 ali, que é um número real. Sim, é, mas também é um número complexo com b = 0. Os números complexos são uma generalização dos números reais.

Até agora, o número imaginário i provavelmente ainda é um mistério para você. O que ele é? Bem, embora possa parecer estranho, ele é definido pela seguinte equação:

i = √(-1),

e isso é tudo o que você precisa para calcular a raiz quadrada de qualquer número, seja ele positivo ou não. Vamos ver alguns exemplos:

• Raiz quadrada de -9: √(-9) = √(-1 · 9) = √(-1)√9 = 3i;
• Raiz quadrada de -13: √(-13) = √(-1 · 13) = √(-1)√13 = i√13; e
• Raiz quadrada de -49: √(-49) = √(-1 · 49) = √(-1)√49 = 7i.

Não é simples? Esse problema não surge com a raiz cúbica, pois você pode obter o número negativo multiplicando três dos números negativos idênticos (o que não é possível fazer com dois números negativos). Por exemplo:

³√(-64) = ³√[(-4) · (-4) · (-4)] = -4.

E isso é tudo o que você precisa saber sobre cálculos envolvendo raízes!