Calculadora de Ângulo Central

Você já se perguntou como encontrar o ângulo central de um círculo? A calculadora de ângulo central está aqui para ajudar; as únicas variáveis que você precisa são o comprimento do arco e o raio.

Continue lendo para saber a definição de ângulo central e como usar a fórmula do ângulo central.

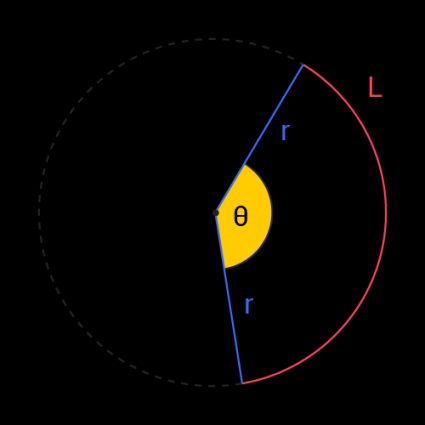
Um ângulo central é um ângulo com um vértice do ângulo no centro de um círculo cujos braços se estendem até a borda da circunferência. Você pode imaginar o ângulo central como sendo a ponta de uma fatia de uma pizza circular grande.

Você pode encontrar o ângulo central de um círculo usando a fórmula:

θ = L / r

onde θ é o ângulo central em radianos, L é o comprimento do arco e r é o raio.

A simplicidade da fórmula do ângulo central se origina da definição de radiano. Um radiano é uma unidade de tamanho angular. Podemos definir 1 radiano como um ângulo central (θ) cujo comprimento do arco é igual ao raio (L = r).

Podemos entender melhor o ângulo central em termos do famoso gráfico pizza. Acredite ou não, as pizzas são ótimas para explicar a matemática de um círculo, como você pode ver em nossa calculadora de tamanho de pizza. Qual seria o ângulo central de uma fatia de pizza se o comprimento da borda ($L$) fosse igual ao raio ($r$)?

Como o problema estabelece que $L = r$, e sabemos que $1$ radiano é definido como o ângulo central quando $L = r$, podemos ver que o ângulo central é $1$ radiano. Você também pode usar a fórmula do ângulo central para obter esse resultado:

Em uma pizza circular completa, sabemos que os ângulos centrais de todas as fatias somarão 2π radianos = 360°. Como cada fatia tem um ângulo central de $1$ radianos, precisaremos de $2\pi / 1 = 2\pi$ fatias ou $6{,}28$ fatias para preencher um círculo completo.

Se você pensar nesse problema em termos da borda da pizza, chegaremos à mesma resposta: a calculadora de circunferência nos informa que o perímetro de um círculo é $2\pi r$. Se o comprimento da borda = raio, então $2\pi r / r = 2\pi$, ou seja, $6{,}28$ fatias caberão ao longo do perímetro da pizza.

Agora, se você ainda estiver com fome, dê uma olhada no calculadora da área do setor circular para calcular a área de cada fatia de pizza!

Tente usar a calculadora de ângulo central ao contrário para ajudar você a resolver esse problema. A Terra está a aproximadamente 149,6 milhões de km de distância do Sol. Se a Terra percorre cerca de um quarto de sua órbita a cada estação, quantos quilômetros ela percorre a cada estação (por exemplo, da primavera ao verão)?

Vamos abordar esse problema passo a passo:

1. Simplifique o problema supondo que a órbita da Terra seja circular (A órbita da Terra é, na verdade, elíptica e muda constantemente). Nesse modelo, o Sol está no centro do círculo e a órbita da Terra é a circunferência.

2. O raio é a distância entre a Terra e o Sol: $149{,}6$ milhões de km.

3. O ângulo central é um quarto de um círculo: $360\degree / 4 = 90\degree$.

4. Use a calculadora de ângulo central para encontrar o comprimento do arco.

Você mesmo pode tentar fazer o cálculo final reorganizando a fórmula como:

Em seguida, converta o ângulo central em radianos $90\degree = 1{,}57\ \mathrm{rad}$ (use nosso conversor de ângulos 🇺🇸 se você não se lembrar como fazer isso) e resolva a equação:

Assim, ao assumimos uma órbita perfeitamente circular, vemos que a Terra percorre aproximadamente 234,9 milhões de km a cada estação!