Calculadora de Intervalo de Confiança

Essa calculadora de intervalo de confiança da Omni é uma ferramenta que o ajudará a encontrar o intervalo de confiança de uma amostra, desde que você forneça a média, o desvio padrão e o tamanho da amostra (consulte também a calculadora de média 🇺🇸 da Omni). Você pode usá-la com qualquer nível de confiança arbitrário. Se você quiser saber o que é exatamente o intervalo de confiança e como calculá-lo, ou se estiver procurando a fórmula do intervalo de confiança de 95% para o escore padrão (escore-z), este artigo certamente o ajudará.

A definição diz que "um intervalo de confiança é o intervalo de valores, derivado de estatísticas amostrais, que provavelmente conterá o valor de um parâmetro populacional desconhecido". Mas o que isso significa na realidade?

Vamos tentar entender com um exemplo: imagine que um fabricante de tijolos esteja preocupado em saber se a massa dos tijolos que ele fabrica está de acordo com as especificações. Ele mediu a massa média de uma amostra de 100 tijolos como sendo igual a 3 kg. Ele também descobriu que o intervalo de confiança de 95% está entre 2,85 kg e 3,15 kg. Isso significa que ele pode ter 95% de certeza de que a massa média de todos os tijolos que fabricar ficará entre 2,85 kg e 3,15 kg. Mais precisamente: se o fabricante de tijolos coletasse muitas amostras de 100 tijolos e usasse cada amostra para calcular o intervalo de confiança, 95% desses intervalos conteriam a verdadeira massa média de um tijolo.

É claro que você nem sempre quer ter exatamente 95% de certeza. Talvez você queira ter 99% de certeza, ou talvez seja suficiente para você que o intervalo de confiança esteja correto em 90% dos casos. Essa porcentagem é chamada de nível de confiança.

O cálculo do intervalo de confiança exige que você conheça três parâmetros da amostra: o valor médio, μ; o desvio padrão, σ; e o tamanho da amostra, n (o número de medições realizadas). Em seguida, você pode calcular o erro padrão (se quiser entender mais sobre esse assunto, confira a calculadora de erro padrão 🇺🇸 da Omni) e, depois, a margem de erro de acordo com as fórmulas a seguir:

erro padrão = σ/√n

margem de erro = erro padrão × Z(0,95)

onde Z(0,95) é o e escore padrão correspondente ao nível de confiança de 95%. Se estiver usando um nível de confiança diferente, você precisará calcular o escore-z apropriado em vez desse valor. Mas não se preocupe, a calculadora de escore padrão z da Omni facilitará isso para você!

Como encontrar o valor Z(0,95)? Este é o valor do escore-z em que o nível de confiança bicaudal é igual a 95%. Isso significa que se você desenhar uma curva de distribuição normal, a área entre os dois escores-z será igual a 0,95 (de 1). E é claro que a Omni também tem uma calculadora de distribuição normal, caso você tenha dúvidas sobre esse assunto.

Se você quiser calcular esse valor usando uma tabela de escore-z, precisará seguir os passos abaixo:

1. Decida qual é o seu nível de confiança. Vamos supor que seja 95%.
2. Calcule qual é a probabilidade de que seu resultado não esteja no intervalo de confiança. Esse valor é igual a 100% - 95% = 5%.
3. Dê uma olhada na curva de distribuição normal. 95% é a área no meio. Isso significa que a área à esquerda do oposto do seu escore-z é igual a 0,025 (2,5%) e a área à direita do seu escore-z também é igual a 0,025 (2,5%).
4. A área à direita do seu escore z é exatamente igual ao valor-p do seu escore z. Você pode usar as tabelas de escore z para encontrar o escore z que corresponde ao valor p de 0,025. Nesse caso, ele é 1,959. A calculadora de valor-p da Omni também é uma ótima ferramenta para entender sobre a estatística dos dados.

Depois de calcular o valor Z(0,95), você pode simplesmente inserir esse valor na equação acima para obter a margem de erro. Agora, você só precisa encontrar os limites inferior e superior do intervalo de confiança:

limite inferior = média - margem de erro

limite superior = média + margem de erro

Para calcular um intervalo de confiança (bilateral), você precisa seguir estas etapas:

1. Digamos que o tamanho da amostra seja 100.
2. Encontre o valor médio de sua amostra. Suponha que seja "3".
3. Determine o desvio padrão da amostra. Digamos que seja "0,5".
4. Escolha o nível de confiança. O nível de confiança mais comum é "95%".
5. Na tabela estatística, encontre o escore-Z(0,95), ou seja, o 97,5° percentil de N(0,1). No nosso caso, esse valor é 1,959.
6. Calcule o erro padrão como σ/√n = 0,5/√100 = 0,05.
7. Multiplique esse valor pelo escore-z para obter a margem de erro: 0,05⋅1,959 = 0,098.
8. Adicione e subtraia a margem de erro do valor médio para obter o intervalo de confiança. No nosso caso, o intervalo de confiança está entre 2,902 e 3,098.

É isso aí! Você fez muitos cálculos, não foi? Felizmente, nossa calculadora de nível de confiança pode realizar todos esses cálculos por conta própria.

Uma maneira peculiar de usar o intervalo de confiança é a análise de série temporal, em que o conjunto de dados de amostra representa uma sequência de observações em um período de tempo específico.

Um assunto frequente desse tipo de estudo é se uma alteração em uma variável pode afetar outra variável.

Para ser mais específico, vamos considerar a seguinte pergunta geral que frequentemente desperta o interesse dos economistas: "Como uma mudança na taxa de juros afeta o nível de preços?"

Há várias maneiras de abordar essa questão, que envolve uma análise teórica e empírica complexa, que está muito além do escopo deste texto. Além disso, há várias técnicas para estimar e aplicar intervalos de confiança. Ainda assim, por meio deste exemplo, podemos representar a funcionalidade do intervalo de confiança em um problema mais complicado.

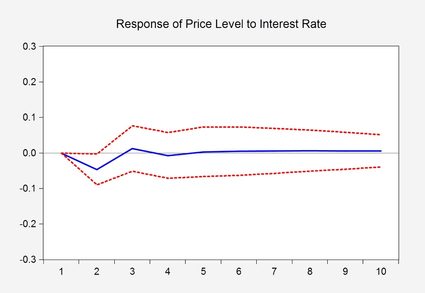
O gráfico acima é uma representação visual de um resultado de estimativa de um modelo econométrico, a chamada Função de Resposta ao Impulso, que mostra a reação de uma variável no caso de uma alteração na outra variável. As linhas vermelhas tracejadas abaixo e acima da linha azul representam um intervalo de confiança de 95% ou, faixa de confiança, que define uma região de resultados mais prováveis. Mais especificamente, isso mostra que, após uma alteração na taxa de juros, é somente no segundo mês que ocorre uma resposta significativa no nível de preço.

Resumindo, esperamos que, com os exemplos e a breve descrição acima, você tenha mais informações sobre a finalidade do intervalo de confiança e se sinta mais confiante para usar nossa calculadora.

Se você coletar amostras repetidamente e usar cada uma delas para encontrar um conjunto de intervalos de confiança de 95% para a média da população, a verdadeira média da população estará contida em cerca de 95% desses intervalos de confiança. Os 5% restantes dos intervalos não conterão a verdadeira média da população.

O escore-z para um intervalo de confiança de 95% bilateral é 1,959, que é o 97,5° percentil da distribuição normal padrão N(0,1).

O escore-z para um intervalo de confiança bilateral de 99% é 2,807, que é o 99,5° percentil da distribuição normal padrão N(0,1).

A largura de um intervalo de confiança aumenta quando a margem de erro aumenta, o que acontece quando:

• O nível de significância aumenta;
• O tamanho da amostra diminui; ou
• A variância da amostra aumenta.

A largura de um intervalo de confiança diminui quando a margem de erro diminui, o que acontece quando:

• O nível de significância diminui;
• O tamanho da amostra aumenta; ou
• A variância da amostra diminui.

A média da amostra não tem impacto sobre a largura de um intervalo de confiança!