Calculadora de Combinação

Esta calculadora de combinações (calculadora r de n itens) é uma ferramenta que ajuda você não apenas a determinar o número de combinações em um conjunto, mas também mostra todas as combinações (ou permutações) possíveis do seu conjunto, de até 20 elementos. No entanto, tenha cuidado! Nosso gerador de combinações pode demorar alguns segundos para encontrar termos muito longos. Se você quiser saber quantas combinações diferentes podem ser feitas com um número específico de elementos e tamanho de amostra, experimente a calculadora de combinações da Omni agora!

Se você ainda não tem certeza do que é uma combinação, tudo será explicado neste artigo. Você encontrará aqui a definição de combinação juntamente com a fórmula da combinação (com e sem repetições). Além disso, mostraremos a você como calcular combinações e o que são a combinação linear e a probabilidade de combinação. Por fim, falaremos sobre a relação entre permutação e combinação. Resumidamente, a permutação considera a ordem dos elementos e a combinação não. Você pode encontrar mais informações abaixo!

Você já se perguntou quais são as suas chances de ganhar o principal prêmio da loteria? E qual é a probabilidade de você ganhar o segundo prêmio? Para responder a essas perguntas e a outras semelhantes, você precisa usar combinações. Temos uma ferramenta especial dedicada a esse tipo de problema. A calculadora de loteria 🇺🇸 da Omni não apenas estima a probabilidade de combinação de ganhar qualquer jogo de loteria, mas também fornece uma fórmula para isso. Experimente! Você poderá descobrir quão grandes (ou pequenos) são esses números.

A combinação é o número de maneiras em que você pode escolher r elementos de um conjunto contendo n objetos distintos. Ao contrário da permutação, a ordem em que você escolhe os elementos, não é essencial. Você pode encontrar uma explicação detalhada sobre este tema na seção permutação e combinação.

Procurar todas as combinações de um conjunto de objetos é um problema puramente matemático. Você provavelmente já aprendeu, por exemplo, como encontrar o maior divisor comum (MDC) ou como encontrar o menor múltiplo comum (MMC). Bem, uma combinação é uma história totalmente diferente. Vejamos quão complicado isso pode ser.

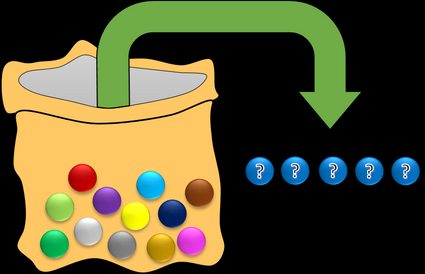
Imagine um saco com doze bolas, sendo que cada uma delas tem uma cor diferente. Você escolhe cinco bolas aleatoriamente. Quantos conjuntos distintos de bolas você pode obter? Ou, em outras palavras, quantas combinações diferentes você pode obter?

Os matemáticos fornecem a solução exata para vários problemas, por exemplo, como calcular área ou volume. Você tem uma abordagem semelhante para estimar o número de combinações no exemplo com as bolas?

Felizmente, você não precisa anotar todos os conjuntos possíveis! Como calcular as combinações, então? Você pode usar a seguinte fórmula de combinação que permitirá determinar o número de combinações em pouco tempo:

onde:

• $C(n,r)$ é o número de combinações;
• $n$ é o número total de elementos no conjunto; e
• $r$ é o número de elementos que você escolhe desse conjunto.

O ponto de exclamação $!$ representa um fatorial. Consulte a calculadora de fatorial 🇺🇸 da Omni para obter mais informações sobre esse tema. A expressão no lado direito também é conhecida como o coeficiente binomial.

Apliquemos essa equação ao nosso problema com as bolas coloridas. Precisamos determinar quantas combinações diferentes existem:

Você pode verificar o resultado com nossa calculadora. Ela também listará todas as combinações possíveis! No entanto, você deve estar ciente de que 792 combinações diferentes já são muitas. Para evitar uma situação em que haja um número excessivo de combinações geradas, limitamos esse gerador de combinações a um número máximo específico de combinações (2000 por padrão). Você pode alterá-lo no modo avançado sempre que quiser.

Você pode notar que, conforme a fórmula de combinações, o número de combinações para escolher apenas um elemento é simplesmente $n$. Por outro lado, se você precisar selecionar todos os elementos, só há uma maneira de fazer isso. Verifiquemos essa propriedade da combinação com nosso exemplo. Você tem o número total de objetos que é $n = 12$. Cada letra exibida nessa calculadora representa uma cor distinta de uma bola, por exemplo, A é vermelha, B é amarela, C é verde e assim por diante. Se você escolher apenas um elemento $r = 1$ desse conjunto, o número de combinações será $12$, porque há 12 bolas diferentes. Porém, se você escolher $r = 12$ elementos, haverá apenas $1$ combinação possível que inclui todas as bolas. Experimente você mesmo com a nossa calculadora!

A esta altura, você provavelmente já sabe tudo o que deveria saber sobre combinações e sobre a fórmula da combinação. Se você acha que ainda pode aprender mais, nas próximas seções, escreveremos mais sobre as diferenças entre permutação e combinação (que muitas vezes são erroneamente consideradas a mesma coisa), probabilidade de combinação e combinação linear.

Imagine que você tenha a mesma sacola cheia de bolas coloridas do exemplo da seção anterior: O que é uma combinação? — definição de combinação. Novamente, você escolhe cinco bolas aleatoriamente, mas, desta vez, a ordem é importante, ou seja, não é o mesmo escolher a bola vermelha como primeira ou terceira opção. Vejamos um exemplo mais simples em que você escolhe três bolas chamadas R (rosa), B (branca) e V (verde). Há seis permutações desse conjunto (a ordem das letras determina a ordem das bolas selecionadas): RBV, RVB, BRV, BVR, VRB, VBR, e a definição de combinação diz que há apenas uma combinação! Essa é a diferença crucial.

Por definição, uma permutação é o rearranjo de todos os membros de um conjunto em alguma sequência ou ordem. No entanto, na literatura, muitas vezes generalizamos esse conceito e renunciamos à exigência de usar todos os elementos em um determinado conjunto. É isso que torna a permutação e a combinação tão semelhantes. Esse significado de permutação determina o número de maneiras pelas quais você pode escolher e organizar r elementos de um conjunto contendo n objetos distintos. Isso é chamado de r-permutações de n (às vezes chamadas de variações). Se você quiser uma explicação ainda mais detalhada, a calculadora de permutação 🇺🇸 da Omni vai tirar todas as suas dúvidas.

A fórmula de permutação é a seguinte:

Essa equação não parece familiar à fórmula da combinação? Na verdade, se você souber o número de combinações, poderá calcular facilmente o número de permutações:

Se você usar o modo avançado desta calculadora de combinações, poderá encontrar o número de permutações.

Você pode estar se perguntando: quando devo usar a permutação em vez de uma combinação?. Bem, isso depende se você precisa ou não levar em conta a ordem. Por exemplo, digamos que você tenha um baralho de nove cartas com dígitos de 1 a 9. Você tira três cartas aleatórias e as alinha na mesa, criando um número de três dígitos, por exemplo, 425 ou 837. Quantos números distintos você pode criar?

Verifique o resultado com a nossa calculadora! E quantas combinações diferentes você tem?

O número de combinações é sempre menor que o número de permutações. Desta vez, ele é seis vezes menor (se você multiplicar 84 por $3! = 6$, obterá 504). Isso decorre do fato de que cada três cartas que você escolher podem ser reorganizadas de seis maneiras diferentes, como no exemplo anterior com as três bolas coloridas.

Para concluir nossas considerações sobre permutação e combinação, temos que introduzir uma seleção semelhante, mas desta vez com repetições permitidas. Isso significa que toda vez que você escolher um elemento do conjunto de n objetos distintos, você o colocará de volta nesse conjunto. No exemplo com as bolas coloridas, você pega uma bola da sacola, lembra-se de qual delas retirou e a coloca de volta na sacola. Analogamente, no segundo exemplo com cartas, você seleciona uma carta, anota o número dessa carta e a coloca de volta no baralho. Dessa forma, você pode ter, por exemplo, duas bolas vermelhas em sua combinação ou 228 como na permutação.

Você provavelmente imagina que ambas as fórmulas serão muito complicadas. Ainda assim, não chegam a ser tão sofisticadas quanto o cálculo do teor alcoólico de sua cerveja caseira. De fato, no caso da permutação, a equação fica ainda mais simples. A fórmula para combinação com repetição é a seguinte:

e para permutação com repetição:

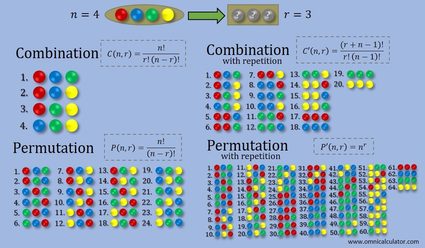
Na figura abaixo, apresentamos um resumo das diferenças entre os quatro tipos de seleção: combinação, combinação com repetição, permutação e permutação com repetição. É um exemplo em que você tem quatro bolas de várias cores e escolhe três delas. No caso de seleções com repetição, você pode escolher uma das bolas várias vezes. Se você quiser tentar com as permutações, tenha cuidado, pois haverá milhares de conjuntos diferentes! No entanto, você ainda pode calcular com segurança quantos deles existem (as permutações estão no modo avançado).

Vamos começar com a probabilidade de combinação, essencial em muitos problemas estatísticos. O exemplo ilustrado acima deve explicar isso facilmente: você escolhe três de quatro bolas coloridas da sacola. Digamos que você queira saber as chances (probabilidade) de haver uma bola vermelha entre elas. Há quatro combinações diferentes, e a bola vermelha está em três delas. A probabilidade de combinação é então:

Se você tirar três bolas aleatórias do saco, em 75% dos casos, você escolherá uma bola vermelha. Para expressar a probabilidade, geralmente usamos o sinal de porcentagem.

Agora, vamos supor que você pegue uma bola, anote a cor que obteve e coloque-a de volta na sacola. Qual é a probabilidade de combinação de você obter pelo menos uma bola vermelha? Esse é um problema de "combinação com repetição". Na figura acima, você pode ver que há vinte combinações no total e que a bola vermelha está em dez delas, portanto:

Esse resultado foi uma surpresa para você? Bem, não deveria ser. Quando você devolve a primeira bola, por exemplo, a bola azul, você pode sacá-la como segunda e terceira bola também. Assim, as chances de você obter uma bola vermelha são menores. Você pode fazer considerações análogas com a permutação. Tente resolver um problema com o saco de bolas coloridas: qual é a probabilidade de que sua primeira bola escolhida seja vermelha?

Digamos que você não confie em nós e queira testar você mesmo. Você tira três bolas de um total de quatro e verifica se há uma bola vermelha ou não (como no primeiro exemplo desta seção). Você repete esse processo mais três vezes e obtém a bola vermelha somente em um dos quatro casos, $25\%$ dos casos. Você esperava $75\%$ de acordo com a teoria. O que aconteceu? Bem, é assim que a probabilidade funciona! Existe a lei dos grandes números que descreve o resultado da realização do mesmo experimento um grande número de vezes. Se você repetir o desenho, por exemplo, cem vezes, estará muito mais próximo de $75\%$.

Além disso, a lei dos grandes números quase sempre leva à distribuição normal padrão, que pode descrever, por exemplo, a inteligência ou a altura das pessoas, com o chamado valor p. Você quer saber mais? A calculadora de distribuição normal é para onde você deve ir!

Você já ouviu falar sobre a combinação linear? Na verdade, apesar de ter a palavra combinação, ela não tem muito em comum com o que aprendemos até agora. Mesmo assim, tentaremos explicá-la brevemente. Uma combinação linear é o resultado de você pegar um conjunto de termos e multiplicar cada termo por uma constante e somar os resultados. Ela é usada com frequência na física de ondas para prever a equação da grade de difração ou mesmo na física quântica por causa da equação de Broglie. Aqui, você pode ver alguns exemplos comuns de combinação linear:

1. Vetores. Todo vetor em 3D pode ser decomposto em três vetores unitários $\^e_1 = (1,0,0)$, $\^e_2 = (0,1,0)$ e $\^e_3 = (0,0,1)$. Por exemplo, $\vec{v} = (2,5,3) = 2\^e_1 + 5\^e_2 + 3\^e_3$ e isso é uma combinação linear.
2. Funções. Digamos que você tenha duas funções $f(x) = \text{e}^x$ e $g(x) = \text{e}^{-x}$. A partir dessas duas funções, você pode criar combinações lineares que descrevem o seno hiperbólico $\sinh(x) = \frac{f(x)}{2} - \frac{g(x)}{2}$ ou cosseno hiperbólico $\cosh(x) = \frac{f(x)}{2} + \frac{g(x)}{2}$. Você pode fazer algo semelhante com o seno e o cosseno normais, mas precisa usar o número imaginário $i$. Falamos mais sobre isso na última seção da calculadora de raiz quadrada.
3. Polinômios. Por exemplo, você tem três polinômios $p_1(x) = 1$, $p_2(x) = 3x + 3$, $p_3(x) = x^2 -x + 1$ e deseja expressar a função $q(x) = 2x^2 + x + 3$ como uma combinação linear desses polinômios. Nem sempre é possível fazer isso, mas, nesse caso, $q(x) = -2p_1(x) + p_2(x) + 2p_3(x)$.

A diferença fundamental entre combinações e permutações em matemática é se nos importamos ou não com a ordem dos itens:

• Na permutação, a ordem é importante, portanto, organizamos os itens em ordem sequencial.
• Nas combinações, a ordem não importa, portanto, selecionamos um grupo de itens de uma coleção maior.

Se você já tiver uma combinação e quiser transformá-la em uma permutação, precisará impor uma ordem no conjunto de itens, ou seja, escolher uma das possíveis ordens para o seu conjunto. Portanto, o número de permutações de r itens escolhidos entre n itens é igual ao número de combinações de r itens escolhidos entre n itens multiplicado pelo número de ordenações desses r itens, ou seja, por r!.

Se você já tiver uma permutação e quiser transformá-la em uma combinação, precisará remover a ordem, ou seja, considerar todas as reordenações possíveis como o mesmo objeto. Portanto, o número de combinações de r itens escolhidos entre n itens é igual ao número de permutações de r itens escolhidos entre n itens dividido pelo número de ordenações desses r itens, ou seja, por r!.

Se a palavra tiver sete letras distintas, você terá 7! = 5040 maneiras de organizá-las (permutações simples de sete itens). Entretanto, se algumas letras aparecerem mais de uma vez, o número de arranjos será reduzido! Por exemplo:

• Se a palavra for "SIMPLES", o "S" aparecerá duas vezes, então dividiremos 7! por 2! = 2 e o resultado é 2520.
• Se a palavra for "SORRISO", temos "S" e "R" aparecendo duas vezes, então dividimos 7! por 2! ⋅ 2! = 4 e o resultado é 1260.
• Se a palavra for "ADAPTAR", temos "A" três vezes, então dividimos 7! por 3! = 6 e o resultado é 840.