Última atualização: 30 de Oct. de 2024

Calculadora de Volume do Tanque

Q: Como calcular o volume de um tanque de água?

Você pode usar a calculadora de volume de tanque da Omni ou fazer o seguinte: Obtenha o raio interno e a altura do tanque . Eleve o raio ao quadrado e, em seguida, multiplique por pi (3,14159...). Pronto, você obteve a área da base do tanque. Multiplique o resultado pela altura e você obterá o volume do tanque .

Q: Como calcular a capacidade do meu motor?

Os especialistas em automóveis chamam isso de deslocamento do motor, e você pode calculá-lo da seguinte forma: Obtenha o volume de um dos cilindros do seu motor. Você pode usar a calculadora de volume do tanque da Omni ou obter o raio e a altura do cilindro (curso do pistão do motor). Eleve o raio ao quadrado , multiplique por pi (3,14159...) e, em seguida, pelo curso do pistão. Multiplique o volume de um cilindro pelo número de cilindros do motor e você obterá a capacidade do motor.

Q: Quanto tempo a água armazenada pode durar em um tanque?

Isso dependerá da quantidade de água que você armazenou e da taxa de vazão. Calcule o volume de seu tanque de água com a calculadora de volume de tanque da Omni. Você obterá o valor em litros. Determine quantos litros você consome por dia . Divida a quantidade de água que você tem pelo seu consumo diário. O resultado é a quantidade de dias de água que você tem.

Q: Por que preferimos tanques de água cilíndricos ao invés de retangulares?

Há dois motivos principais pelos quais preferimos tanques cilíndricos a tanques retangulares: Os tanques cilíndricos são melhores para resistir à tensão do que os retangulares. Assim, os fabricantes precisam de menos material para construí-los. Os tanques retangulares são mais difíceis de limpar , especialmente nos cantos.

Q: Qual é o volume de um barril de petróleo?

218,7 litros. Um barril de petróleo tem um diâmetro de 0,572 m e uma altura de 0,851 m. Coloque esses números na seguinte fórmula: Volume = π⋅h⋅(d/2)² = 3,141⋅0,851(0,572/2)² = 0,2187 m² = 218,7 litros

Criada por Dr.(a) Hanna Pamuła

Revisada por Bogna Szyk e Jack Bowater

Traduzida por Doutorando(a), Marinara Andrade do Nascimento Moura

Marinara Andrade do Nascimento Moura

PhD candidate

LinkedInWebsiteResearch Gate

Marinara holds a master’s degree in Technology and is working on her PhD in Civil Engineering. She has always been interested in science and engineering, mostly because she is passionate about solving problems. She has published her articles in important scientific journals and international conferences as a researcher. She has experience teaching undergraduate students and believes that teaching is a perfect way to learn because the more we give, the more we have. In her free time, she loves to cook (and eat!), travel with her husband, and chat with her friends. See full profile

Check our editorial policy

e Dr.(a) João Rafael Lucio dos Santos

João Rafael Lucio dos Santos

PhD, Federal University of Campina Grande

LinkedInWebsiteResearch Gate

Joao is a physicist, researcher, and professor in Brazil. He earned his Ph.D. in Physics at the University of Rochester, NY in 2013. He has written several papers in international journals, mainly in field theory and cosmology. Joao is also a researcher and the outreach leader for the BINGO telescope. This state-of-the-art radio telescope will be operating in the Northeast of Brazil in a few years. He believes in the importance of spreading knowledge and high-quality information among society and the public in general. He also believes that people can enjoy the learning process if it is funny and if they can see it as a path to change their life, even in daily activities. In his free time, he enjoys running, playing tennis, cooking, traveling, and having pleasant moments with his relatives and friends. See full profile

Check our editorial policy

Novo

Índice

Como usar a calculadora de volume do tanque Fórmula do volume do tanque cilíndrico Calculadora de volume de tanque retangular (prisma retangular)Fórmula para o volume de uma cápsula Volume do tanque elíptico Volume do tronco de cone: tanque em forma de funil Volume do tanque de fundo e topo cônico Perguntas frequentes

Com essa calculadora de volume do tanque da Omni, você pode facilmente estimar o volume do seu tanque. Você pode escolher entre dez formatos diferentes de tanque: desde tanques retangulares e cilíndricos padrão até tanques em formato de cápsula e elípticos. Você pode até mesmo encontrar o volume de tanques em formato de cone trucando ou de topo ou fundo cônico. Basta inserir as dimensões do seu tanque e essa ferramenta calculará o volume total do tanque para você. Você também pode fornecer a altura de preenchimento, que será usada para encontrar o volume do tanque preenchido.

Você quer saber como ela faz isso? Continue lendo e você encontrará todas as fórmulas de que precisa: o volume de um tanque de cápsula, tanque elíptico ou os amplamente utilizados tanques de fundo cônico (às vezes chamados de tanques cônicos), além de muitos outros!

Você está procurando outros tipos de tanques em diferentes formatos e para outras aplicações? Confira nossa calculadora de volume para que você encontre o volume dos sólidos tridimensionais mais comuns. Para algo mais específico, você também pode dar uma olhada na calculadora de aquários e na calculadora de piscina, ambas ferramentas da Omni, onde você poderá obter o volume de objetos usados na sua vida cotidiana.

Como usar a calculadora de volume do tanque

Essa calculadora de volume de tanque é uma ferramenta simples que ajuda você a encontrar o volume do tanque, bem como o volume da parte preenchida. Você pode escolher entre dez formatos de tanques diferentes:

Cilindro vertical;
Cilindro horizontal;
Prisma retangular (caixa);
Cápsula vertical;
Cápsula horizontal;
Elíptico vertical;
Elíptico horizontal;
Fundo cônico;
Topo cônico; e
Tronco de cone (em forma de funil).

"Mas como eu uso essa calculadora de volume de tanque?", você pode estar se perguntando. Vamos dar uma olhada em um exemplo simples:

Decida a forma. Vamos supor que você queira encontrar o volume de um tanque tipo cilindro vertical - escolha essa opção na lista suspensa. A imagem esquemática do tanque aparecerá abaixo; certifique-se de que é a que você deseja!
Digite as dimensões do tanque. No nosso caso, precisamos digitar o comprimento e o diâmetro. Em nosso exemplo, eles são iguais a $32\ \mathrm{cm}$ e $24\ \mathrm{cm}$ , respectivamente. Além disso, podemos digitar a altura de preenchimento: $28\ \mathrm{cm}$ .
A calculadora de volume do tanque já encontrou o volume total e o volume preenchido! O volume total do tanque é $14{,}48\ \mathrm{L}$ , e o volume do líquido no interior é $12{,}67\ \mathrm{L}$ . Como sempre, com as ferramentas Omni você pode alterar as unidades clicando nas próprias unidades de volume.

Fórmula do volume do tanque cilíndrico

Para calcular o volume total de um tanque cilíndrico, tudo o que precisamos saber é o diâmetro do cilindro (ou raio) e a altura do cilindro (que pode ser chamada de comprimento se ele estiver na horizontal).

Tanque cilíndrico vertical

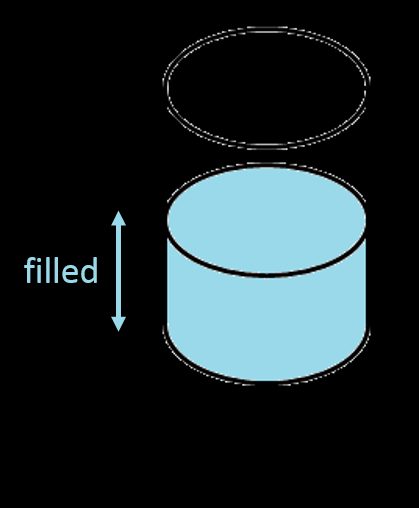
Tanque de cilindro vertical com dimensões.

Podemos encontrar o volume total de um tanque cilíndrico com a fórmula padrão de volume, ou seja, a área da base multiplicada pela altura. Um círculo é a forma da base, portanto sua área, de acordo com a conhecida equação, é igual a $\pi \cdot \mathrm{raio}^2$ . Deste modo, a fórmula para o volume de um tanque cilíndrico vertical é a seguinte:

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro \ vertical}}} &= \pi \cdot r^2 \cdot h\\[.6em] &=\pi\cdot\left(\frac{d}{2}\right)^2\cdot h, \end{split}

onde:

$r$ é o raio da base; e
$h$ é a altura do cilindro.

Se quisermos calcular o volume preenchido, precisaremos encontrar o volume de um cilindro "mais curto", que também é muito fácil!

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro\ vertical}}} &= \pi \cdot r^2 \cdot f\\[.6em] &=\pi\cdot\left(\frac{d}{2}\right)^2\cdot f, \end{split}

onde $f$ é a altura da parte preenchida do cilindro.

Tanque de cilindro horizontal

O volume total de um tanque cilíndrico horizontal pode ser encontrado de forma análoga, ou seja, é a área da extremidade circular vezes o comprimento do cilindro:

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro \ horizontal}}} &= \pi \cdot r^2 \cdot l\\[.6em] &=\pi\cdot\left(\frac{d}{2}\right)^2\cdot l, \end{split}

onde $l$ é o comprimento do cilindro.

Seção transversal de um tanque cilíndrico parcialmente cheio.

As coisas ficam mais complicadas quando queremos encontrar o volume do cilindro horizontal parcialmente preenchido. Primeiro, precisamos encontrar a área da base: a área do segmento circular preenchida pelo líquido:

A_{\mathrm{\tiny segmento}} = \frac{1}{2}\cdot r^2 \cdot (\theta-\sin(\theta)),

onde $r$ é o raio da base e $\theta$ é o ângulo central do segmento. O ângulo $\theta$ pode ser encontrado com a fórmula do cosseno:

\cos\left(\frac{\theta}{2}\right) = \frac{r-f}{f},

em que $f$ é a altura da seção preenchida da base.

Portanto:

\theta= 2\cdot \arccos\left(\frac{r-f}{f}\right)

E, finalmente, a fórmula para o volume de um cilindro horizontal parcialmente preenchido $V_{\scriptsize{\mathrm{chf}}}$ é:

\small V_{\scriptsize{\mathrm{chf}}} = 0{,}5\cdot r^2\cdot(\theta -\sin(\theta))\cdot l,

onde:

\theta = 2\cdot \arccos\left(\frac{r-f}{r}\right)

Se mais da metade do cilindro estiver preenchida, será mais fácil subtrair a parte vazia do tanque do volume total.

Calculadora de volume de tanque retangular (prisma retangular)

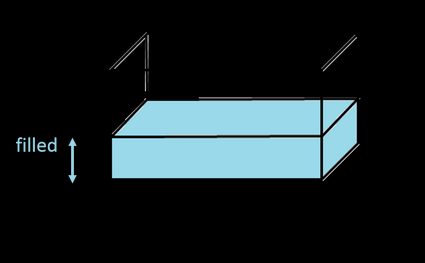
Tanque retangular com dimensões marcadas.

Se você está se perguntando como calcular o volume de um tanque retangular (também conhecido como prisma retangular, caixa ou hexaedro retangular), não precisa mais procurar! Talvez você conheça esse tanque como tanque retangular, mas esse não é o nome correto, pois um retângulo é uma forma 2D e, portanto, não tem volume.

Para encontrar o volume do prisma retangular, multiplique todas as dimensões do tanque:

V_{{\mathrm{prisma\ retangular}}} = h\cdot w\cdot l,

onde:

$h$ é a altura do tanque;
$w$ é a largura; e
$l$ é o comprimento do tanque.

Se você quiser saber qual é o volume do líquido neste tanque, basta alterar a variável altura para preenchido na fórmula do volume do tanque retangular. Assim, o volume de um prisma retangular preenchido, $V_{\scriptsize{\mathrm{prf}}}$ , é:

V_{{\mathrm{prf}}} = f\cdot w\cdot l,

onde $f$ é a altura da parte preenchida.

Para esta calculadora de volume de tanque, não importa se o tanque está em uma posição horizontal ou vertical. Apenas se certifique de que os parâmetros preenchido e altura estejam ao longo do mesmo eixo.

Fórmula para o volume de uma cápsula

Nossa ferramenta define uma cápsula como dois hemisférios separados por um cilindro. Para calcular o volume total de uma cápsula, tudo o que você precisa fazer é adicionar o volume da esfera à parte do cilindro:

V_{\scriptsize{\mathrm{cap}}} = \pi\!\cdot\!\! \left(\frac{d}{2}\right)^2\!\!\!\cdot\!\left(\frac{4}{3}\!\cdot\!\frac{d}{2}\!+\!l\right)

Dependendo da posição do tanque, os cálculos do volume preenchido serão um pouco diferentes:

1. Para tanque de cápsula horizontal

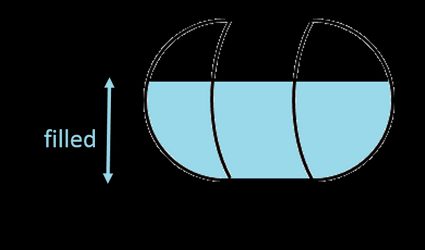
Tanque de cápsula horizontal com dimensões marcadas.

Como os hemisférios em cada extremidade do tanque são idênticos, eles formam uma tampa esférica: some essa parte $V_{\scriptsize{\mathrm{esf\ hf}}}$ à parte do cilindro horizontal $V_{\scriptsize{\mathrm{chf}}}$ (verifique o parágrafo acima) para calcular o volume do líquido em uma cápsula horizontal preenchida ( $V_{\scriptsize{\mathrm{cap\ hf}}}$ ):

\begin{split} &V_{\scriptsize{\mathrm{cap\ hf}}} = V_{\scriptsize{\mathrm{chf}}}+V_{\scriptsize{\mathrm{esf\ hf}}}\\[.6em] &= \frac{1}{2}\!\cdot\!\! \left(\frac{d}{2}\right)^2\!\!\! \cdot\! (\theta-\sin(\theta))\cdot l \\[1em] &\quad+\frac{\pi\cdot f^2}{3}\!\cdot\!\left(\frac{3}{2}\cdot d-f\right), \end{split}

onde:

$d$ é o diâmetro do tanque;
$f$ é a altura preenchida; e
$\theta$ é o ângulo correspondente ao setor preenchido no tanque do cilindro.

2. Para tanque de cápsula vertical

A fórmula é diferente para várias alturas de preenchimento. Em todas as próximas fórmulas, encontraremos estas quantidades:

$d$ é o diâmetro do tanque;
$f$ é a altura alcançada pelo líquido; e
$l$ é o comprimento da seção cilíndrica.

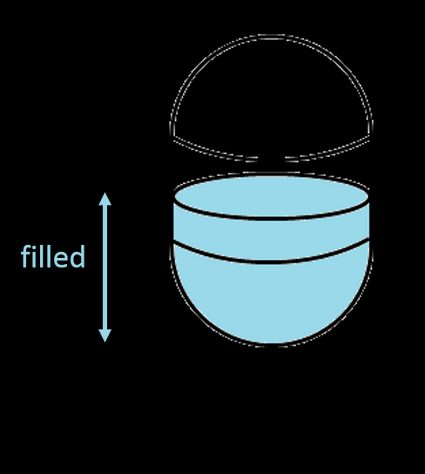
Tanque de cápsula vertical com dimensões marcadas.

Se $f < d/2$ , então, o líquido está apenas na parte inferior do hemisfério, portanto, precisamos apenas da fórmula do volume de uma tampa esférica:

\\[2em] V_{\scriptsize{\mathrm{cap\ f}}} = \frac{(\pi\!\times \!f)^2}{3}\!\times\!\left(\frac{3}{2}\!\times \!d - f\right) \\[2em]

Se $d/2 < f < d/2 +l$ , então, precisamos adicionar o volume do hemisfério e do cilindro "mais curto":

\quad\ \ \ \begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = \frac{2}{3}\cdot \pi\left(\frac{d}{2}\right)^3\\[1em] &\qquad+\pi\cdot\left(\frac{d}{2}\right)^2\cdot\frac{f-d}{2} \end{split}

Se $d/2 + l < f$ , isso significa que temos um hemisfério inferior preenchido e um cilindro, portanto, só precisamos subtrair a tampa esférica (parte vazia) do volume total:

\begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = V_{\scriptsize{\mathrm{cap}}}\! -\! \frac{\pi\cdot(l+d-f)^2}{3}\\ &\qquad\ \ \cdot\left(\frac{3}{2}\cdot d - (l+d-f)\right) \end{split}

Volume do tanque elíptico

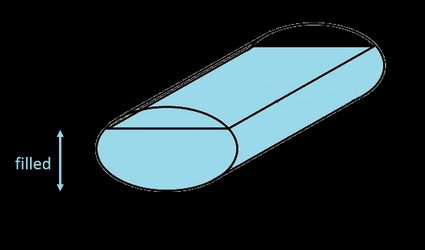
Tanque elíptico horizontal com dimensões marcadas.

Em nossa calculadora, definimos um tanque elíptico como um tanque cilíndrico com extremidades elípticas. Para encontrar o volume total de um tanque elíptico, você precisa multiplicar a área da elipse pelo comprimento do tanque:

V_{\scriptsize{\mathrm{elíptico}}} = \pi\!\cdot\!w\!\cdot\!l\!\cdot\!\frac{h}{4},

onde:

$w$ é a largura do tanque;
$h$ é a altura do tanque; e
$l$ é o comprimento do tanque.

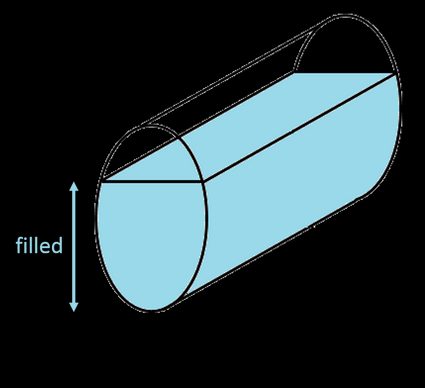
Tanque elíptico vertical com dimensões marcadas.

Finalmente, outra fórmula fácil! Infelizmente, encontrar o volume de um tanque elíptico parcialmente preenchido, tanto na posição horizontal quanto na vertical, não é tão simples. Você precisa usar a fórmula para a área do segmento da elipse e multiplicar o resultado pelo comprimento do tanque:

\begin{split} &V_{\scriptsize{\mathrm{el\ f}}} = l\!\cdot\!h\!\cdot\!\frac{w}{4}\\[1em] &\qquad\cdot\!\left[\arccos\left(1\!-\!\frac{2\!\cdot\!f}{h}\right)\right.\\[1.5em] &\!\!\left.-\!\left(\!1\!-\!\frac{2\!\cdot\!f}{h}\!\right)\!\cdot\!\sqrt{\frac{4\!\cdot\!f}{h}\!-\!\frac{4\!\cdot\!f^2}{h^2}}\right] \end{split}

Volume do tronco de cone: tanque em forma de funil

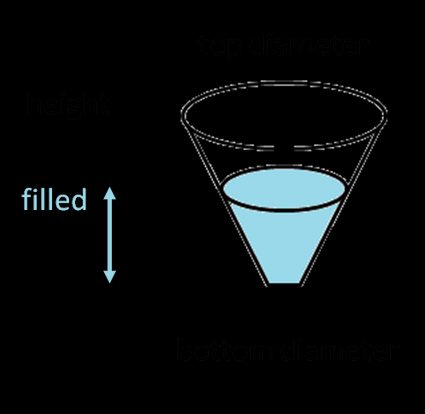
Tanque de tronco de cone com dimensões marcadas.

Para calcular o volume do cone em forma de funil (uma forma específica que conhecemos em nossa calculadora do tronco de um cone 🇺🇸), use a fórmula:

\begin{split} &V_{\scriptsize{\mathrm{tronco}}} = \frac{1}{3}\cdot\pi\cdot h_{\mathrm{cone}}\\[1em] &\qquad\cdot\left( \left(\frac{d_{\mathrm{sup}}}{2}\right)^2\!+\! \frac{d_{\mathrm{sup}}}{2}\!\cdot\!\frac{d_{\mathrm{inf}}}{2}\!\right.\\[1em] &\qquad\qquad \left.+\!\left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right), \end{split}

onde:

$d_{\mathrm{sup}}$ é o diâmetro superior do tronco de cone;
$d_{\mathrm{inf}}$ é o diâmetro inferior do tronco de cone;
$h_{\mathrm{cone}}$ é a altura do tanque.

Tanque cônico com dimensões marcadas e nível de líquido.

Se você quiser encontrar o volume do tronco cônico parcialmente preenchido para uma determinada altura de preenchimento, calcule primeiro o raio superior da parte preenchida:

R = \frac{1}{2} \cdot d_{\mathrm{sup}}\cdot \frac{f+z}{h_{\mathrm{cone}}+z},

onde:

z = h_\mathrm{cone} \cdot \frac{d_{\mathrm{inf}}}{d_{\mathrm{sup}}-d_{\mathrm{inf}}}

(Você pode derivar a fórmula a partir da similaridade dos triângulos)

Depois disso, basta encontrar o novo volume do tronco de cone:

\begin{split} &V_{\scriptsize{\mathrm{tf}}}=\frac{1}{3} \cdot \pi \cdot f \\ &\ \ \cdot \!\left(R^2 \!+ \!R\! \cdot \!\frac{d_{\mathrm{inf}}}{2} + \left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right) \end{split}

Volume do tanque de fundo e topo cônico

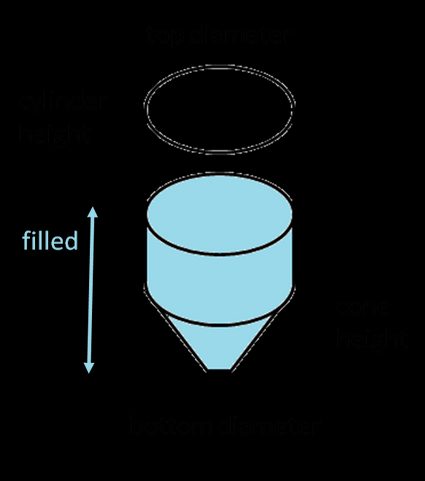
Tanque de fundo cônico com dimensões marcadas.

Encontrar o volume total de um tanque de fundo cônico não é tão difícil, basta somar o volume da parte do tronco de cone ao volume da parte cilíndrica:

\begin{split} &V_{\scriptsize{\mathrm{cone\ b}}} = V_{\scriptsize{\mathrm{tronco}}} + V_{\scriptsize{\mathrm{cilindro}}}\\[1em] & =\frac{1}{3}\times\pi\cdot h_{\mathrm{cone}} \cdot\left( \left(\frac{d_{\mathrm{sup}}}{2}\right)^2\right.\\[1.4em] &\qquad \left.+ \frac{d_{\mathrm{sup}}}{2}\!\cdot\!\frac{d_{\mathrm{inf}}}{2}\!+\!\left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right)\\[1.4em] &\qquad+\pi\cdot\left(\frac{d_{\mathrm{sup}}}{2}\right)^2\cdot h_{\mathrm{cilindro}}, \end{split}

onde:

$d_{\mathrm{sup}}$ é o diâmetro superior do tronco de cone;
$d_{\mathrm{inf}}$ é o diâmetro inferior do tronco de cone;
$h_{\mathrm{cone}}$ e $h_{\mathrm{cilindro}}$ são as alturas dos dois tanques.

Para calcular o tanque parcialmente preenchido, basta adicionar a parte do cilindro e a parte do tronco cônico, dependendo do nível do líquido preenchido, e utilizar as equações acima.

O cálculo do volume total do tanque de topo cônico é exatamente o mesmo que o do tanque de fundo cônico. A única diferença é quando você deseja encontrar a parte preenchida. É claro que, primeiro, a parte cilíndrica é preenchida e, só depois, a parte do tronco de cone.

🙋 Você calculou todos os seus volumes usando unidades métricas, mas precisa das imperiais? Não se preocupe, pois a Omni tem uma solução prática para todas as suas necessidades: use nossa ferramenta conversor de volume 🇺🇸 para converter rapidamente entre unidades de volume!

Perguntas frequentes

Como calcular o volume de um tanque de água?

Você pode usar a calculadora de volume de tanque da Omni ou fazer o seguinte:

Obtenha o raio interno e a altura do tanque.
Eleve o raio ao quadrado e, em seguida, multiplique por pi (3,14159...). Pronto, você obteve a área da base do tanque.
Multiplique o resultado pela altura e você obterá o volume do tanque.

Como calcular a capacidade do meu motor?

Os especialistas em automóveis chamam isso de deslocamento do motor, e você pode calculá-lo da seguinte forma:

Obtenha o volume de um dos cilindros do seu motor. Você pode usar a calculadora de volume do tanque da Omni ou obter o raio e a altura do cilindro (curso do pistão do motor).
Eleve o raio ao quadrado, multiplique por pi (3,14159...) e, em seguida, pelo curso do pistão.
Multiplique o volume de um cilindro pelo número de cilindros do motor e você obterá a capacidade do motor.

Quanto tempo a água armazenada pode durar em um tanque?

Isso dependerá da quantidade de água que você armazenou e da taxa de vazão.

Calcule o volume de seu tanque de água com a calculadora de volume de tanque da Omni. Você obterá o valor em litros.
Determine quantos litros você consome por dia.
Divida a quantidade de água que você tem pelo seu consumo diário. O resultado é a quantidade de dias de água que você tem.

Por que preferimos tanques de água cilíndricos ao invés de retangulares?

Há dois motivos principais pelos quais preferimos tanques cilíndricos a tanques retangulares:

Os tanques cilíndricos são melhores para resistir à tensão do que os retangulares. Assim, os fabricantes precisam de menos material para construí-los.
Os tanques retangulares são mais difíceis de limpar, especialmente nos cantos.

Qual é o volume de um barril de petróleo?

218,7 litros. Um barril de petróleo tem um diâmetro de 0,572 m e uma altura de 0,851 m. Coloque esses números na seguinte fórmula:

Volume = π⋅h⋅(d/2)² = 3,141⋅0,851(0,572/2)² = 0,2187 m² = 218,7 litros