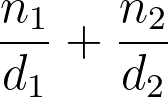Kalkulator ułamków

Witaj w naszym kalkulatorze ułamków, naprawdę wszechstronnym narzędziu. Potrafi ono:

• ➕ dodawać,
• ➖ odejmować,
• ✖️ mnożyć,
• ➗ dzielić dowolne dwa ułamki.

Co więcej, ma możliwość skracania ułamka (tzn. jego upraszczania, redukowania), a także powie ci, jak zamienić ułamek zwykły na ułamek dziesiętny i odwrotnie. Jeśli wciąż nie jesteś pod wrażeniem, to narzędzie działa nie tylko na standardowych ułamkach właściwych i niewłaściwych, ale także na ułamkach mieszanych — czego chcieć więcej? 😁

Jak zwykle, przygotowaliśmy kilka artykułów wprowadzających, które pozwolą ci zagłębić się w świat ułamków 🌎. Poniżej przeczytasz o definicji ułamka, rodzajach ułamków (właściwe, niewłaściwe, mieszane) i wszystkich podstawowych działaniach na ułamkach zwykłych i mieszanych. Czy jesteś gotowy/a?

Ułamek reprezentuje liczbę równych części całości.
Możesz rozpoznać ułamek zwykły, ponieważ zawiera dwie liczby oddzielone linią (lub ukośnikiem):

• Górną liczbę nazywamy licznikiem (ang. numerator) i zapisujemy ją nad kreską. Mówi nam ona:

  Ile mamy części.

• Dolną liczbę nazywamy mianownikiem (ang. denominator) i wyświetlamy ją poniżej linii. Oznacza ona:

  Całkowitą liczbę części.

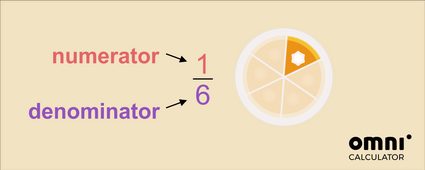
W powyższym przykładzie jest to jeden plasterek z potencjalnych sześciu, na które ciasto zostało pokrojone. Odczytujemy to jako jedną szóstą całego ciasta.

Ale oczywiście ciasto można pokroić inaczej!

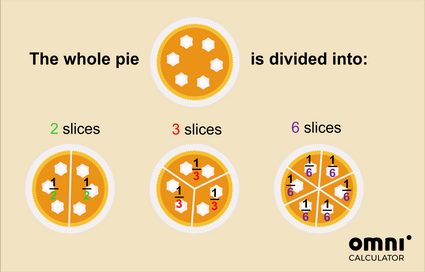
Tak więc, jeśli pokroisz ciasto na 2 części, to jeden kawałek stanowi połowę całości. Jeśli pokroisz ciasto na 3 części, wówczas jeden kawałek stanowi jedną trzecią całego ciasta itd.

Ułamki są używane wszędzie wokół nas:

• Za każdym razem, gdy chcesz wyrazić część całego przedmiotu, który można podzielić na równe kawałki: jak ciasto 🍰, tabliczka czekolady 🍫, arbuz 🍉, pizza 🍕, itd.

• Kiedy coś mierzymy 📏 lub ważymy, zwłaszcza w kilogramach.

• Rozmiar ekranu twojego komputera 🖥️ jest wyrażony jako stosunek, np. 16:9 — i jest to również ułamek, tylko zapisany w inny sposób. (Aby dowiedzieć się, jak uprościć proporcje, sprawdź nasz kalkulator proporcji 🇺🇸!)

Teraz gdy znasz już definicję ułamka, przyjrzyjmy się różnym typom ułamków. Ogólnie rzecz biorąc, mamy trzy rodzaje ułamków: ułamki właściwe, niewłaściwe i mieszane:

1. Ułamki właściwe

   W ułamkach właściwych liczba górna (licznik) jest mniejsza od liczby dolnej (mianownik). Oznacza to, że zawsze będzie mniejsza niż jedna całość, np.

   🍰 5 kawałków z ciasta, które zostało pokrojone na 6.

   🍫 2 rzędy z całej tabliczki czekolady, która ma 5 rzędów.

   🍊 7 części pomarańczy z całej pomarańczy pokrojonej na 8 części.

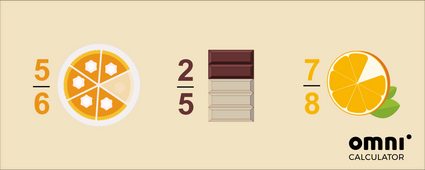
Ogólna zasada, która działa zarówno dla liczb dodatnich, jak i ujemnych, mówi, że wartość bezwzględna ułamka jest mniejsza niż jeden:

|^licznik/_mianownik| < 1

2. Ułamki niewłaściwe

   Czym jest ułamek niewłaściwy? Jest to ułamek, w którym licznik jest większy niż mianownik. Przykładami ułamków niewłaściwych są:

   🍰 10 kawałków ciasta, gdy każde ciasto ma 6 kawałków.

   🍫 8 rzędów tabliczki czekolady. Cała tabliczka czekolady ma 5 rzędów.

   🍊 21 części pomarańczy, jeśli każdą pomarańczę pokroimy na 8 równych części.

3. Ułamki mieszane

   Ułamki mieszane, znane również jako cyfry mieszane lub liczby mieszane, to inny sposób wyrażenia ułamka niewłaściwego. Są to liczby całkowite (liczba całości) i ułamek właściwy razem wzięte. Przyjrzyjmy się zatem przykładom z poprzedniego akapitu:

   🍰 10 kawałków ciasta, gdy każde ciasto ma 6 kawałków to to samo co → 1 całe ciasto i 4 kawałki z 6.

   🍫 8 rzędów czekolady, gdy cała tabliczka czekolady ma 5 rzędów → 1 cała tabliczka czekolady i 3 rzędy z 5.

   🍊 21 części pomarańczy, jeśli pomarańczę pokroimy na 8 plasterków → 2 całe pomarańcze i 5 plasterków z 8.

Jeśli chodzi o dodawanie ułamków, istnieją trzy scenariusze:

1. Mianownik (dolna liczba) jest taki sam w obu ułamkach — np. ³/₅ i ¹/₅

   Jest to najprostszy przypadek; wszystko, co musisz zrobić, to dodać do siebie liczniki (górne liczby) i pozostawić mianownik bez zmian, np.

   ➽ ³/₅ + ¹/₅ = ^{(3 + 1)}/₅ = ⁴/₅

2. Ułamki mają różne mianowniki — np. ²/₅ i ³/₁₀

   Jest to nieco bardziej skomplikowany przypadek — aby dodać te ułamki, musisz znaleźć ich wspólny mianownik.

   • Możesz użyć na przykład NWW — najmniejszej wspólnej wielokrotności, aby znaleźć wspólną liczbę dwóch mianowników: NWW(5,10) = 10. Inną opcją jest pomnożenie mianowników i późniejsze skrócenie (zredukowanie) ułamka.

   • Następnie musisz rozwinąć każdy ułamek, aby mieć ten wspólny mianownik jako dolną liczbę:

   Tak więc musisz pomnożyć ułamek o mianowniku równym 5 (nasze 1/5) przez 2, aby otrzymać 10 (pamiętaj, że musisz pomnożyć zarówno górną, jak i dolną liczbę):

   ➽ ²/₅ = ^{(2 ⋅ 2)}/_{(5 ⋅ 2)} = ⁴/₁₀

   Twój drugi ułamek ma już mianownik równy 10:

   ➽ ³/₁₀

   • Teraz gdy twoje ułamki mają ten sam mianownik, możesz je dodać:

     ➽ ⁴/₁₀ + ³/₁₀ = ^{(4 + 3)}/₁₀ = ⁷/₁₀

3. Chcesz dodać dwa ułamki mieszane — np. 2 ³/₅ i 1 ¹/₂

   Jednym z rozwiązań tego typu problemów jest przelicznik ułamka mieszanego na ułamek niewłaściwy i zsumowanie ich w zwykły sposób.

   Wykonajmy tę operację dla 2 ³/₅

   • Pomnóż liczbę całkowitą przez mianownik:

     2 ⋅ 5 = 10

   • Dodaj wynik do licznika:

     10 + 3 = 13

   • To twój nowy licznik — zapisz go nad mianownikiem:

     2 ³/₅ = ¹³/₅

   Analogicznie możesz sprawić, że 1 ¹/₂ = ³/₂.

   • Wykonaj standardowe dodawanie ułamków o różnych mianownikach:

     ➽ ¹³/₅ + ³/₂ = ²⁶/₁₀ + ¹⁵/₁₀ = ⁴¹/₁₀

   • Na koniec możesz przeliczyć wynik z powrotem na ułamek mieszany:

     Wykonaj dzielenie z resztą:

     ➽ ⁴¹/₁₀ = 4 R 1 = 4 ¹/₁₀

Oczywiście nasz kalkulator ułamków radzi sobie ze wszystkimi tymi scenariuszami. 😎

Jeśli nadal zastanawiasz się, jak działa dodawanie ułamków, może pomoże ci ta grafika?

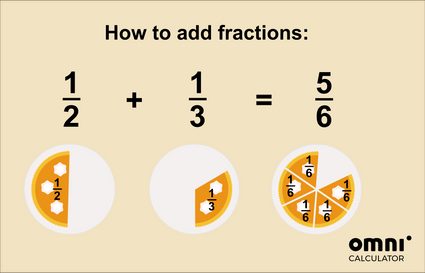
Aby uzyskać jeszcze dokładniejsze wyjaśnienie, sprawdź nasz kalkulator dodawania ułamków 🇺🇸.

Jeśli zastanawiasz się, jak odejmować ułamki i przeczytałeś/aś poprzednią sekcję Jak dodawać ułamki, mamy dla ciebie dobrą wiadomość: to prawie to samo!

1. Jeśli masz ułamki o tym samym mianowniku, odejmij ich liczniki:

   ➽ ³/₅ - ¹/₅ = ^{(3 - 1)}/₅ = ²/₅

2. Podczas odejmowania ułamków o różnych mianownikach — ²/₅ i ³/₁₀ — powtórz procedurę z poprzedniej sekcji, ale w ostatnim kroku odejmij zamiast dodawania:

   • Znajdź wspólny mianownik — to 10.

   • Rozwiń ułamki do ich odpowiedników o wspólnym mianowniku: ⁴/₁₀ i ³/₁₀.

   • Odejmij liczniki.

     ➽ ²/₅ - ³/₁₀ = ⁴/₁₀ - ³/₁₀ = ¹/₁₀

3. Dla ułamków mieszanych (2³/₅ i 1 ¹/₂):

   • Zamień ułamki mieszane na ułamki niewłaściwe tak jak poprzednio:

     2 ³/₅ = ¹³/₅ i 1 ¹/₂ = ³/₂

   • Odejmij dwa ułamki niewłaściwe o różnych mianownikach:

     ➽ ¹³/₅ - ³/₂ = ²⁶/₁₀ - ¹⁵/₁₀ = ¹¹/₁₀

   • Pozostaw ułamek niewłaściwy lub przelicz go z powrotem na ułamek mieszany:

     ➽ ¹¹/₁₀ = 1 R 1 = 1 ¹/₁₀

Możesz wyobrazić sobie odejmowanie jako zabranie lub zjedzenie części tortu:

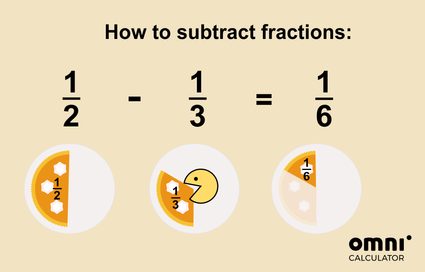
To nie było takie trudne, prawda?

Mnożenie ułamków jest — na szczęście — łatwą operacją. To po prostu działanie licznik razy licznik przez mianownik razy mianownik. Czasami musisz również uprościć ułamek. I to wszystko!

Spójrz na poniższy przykład:

➽ ²/₃ ⋅ ⁵/₆ = ^{(2 ⋅ 5)}/_{(3 ⋅ 6)} = ¹⁰/₁₈

co możesz następnie skrócić do ⁵/₉.

Ilekroć masz do czynienia z ułamkami mieszanymi, nie zapominaj, że zawsze musisz zapisać je jako liczbę niewłaściwą przed pomnożeniem:

➽ 2 ¹/₂ ⋅ 3 ¹/₄ = ⁵/₂ ⋅ ¹³/₄ = ^{(5 ⋅ 13)}/_{(2 ⋅ 4)} = ⁶⁵/₈ = 8 ¹/₈

A kiedy mnożysz ułamek przez liczbę całkowitą, pamiętaj, że możesz zapisać liczbę całkowitą jako samą siebie podzieloną przez 1:

➽ 3 ⋅ ⁵/₇ = ³/₁ ⋅ ⁵/₇ = ^{(3 ⋅ 5)}/_{(1 ⋅ 7)} = ¹⁵/₇

Jeśli nie wiesz, jak poradzić sobie z redukcją ułamków, przewiń w dół do sekcji Jak skracać ułamki.

Teraz gdy już wiesz, jak mnożyć ułamki, przejdźmy do następnego tematu, czyli dzielenia ułamków.

Zastanawiasz się, jak dzielić ułamki? Nie martw się! Dzielenie ułamków jest dość podobne do ich mnożenia. Jedyną różnicą jest to, że musisz pomnożyć pierwszą liczbę przez odwrotność drugiego ułamka. Może to brzmieć trochę dziwnie, ale to naprawdę proste! Spójrz na poniższy przykład:

(¹/₂) / (³/₅) = ¹/₂ ⋅ ⁵/₃ = ^{(1 ⋅ 5)}/_{(2 ⋅ 3)} = ⁵/₆

Wszystko, co musisz zrobić, to odwrócić drugi ułamek do góry nogami (czyli stworzyć jego odwrotność) i pomnożyć ułamki. Czasami możesz również potrzebować skrócenia ułamków. I to wszystko, tadaaa! 🎉

Zawsze lubimy upraszczać sobie życie — nawet w matematyce. Dlatego skracanie (upraszczanie) ułamków jest tak ważną rzeczą. Oznacza to, że zapisujemy ułamek w jego najprostszej możliwej formie. Skracanie ułamków nazywamy również redukcją ułamków.

Ale co to dokładnie oznacza? Spójrz na poniższe przykłady:

• Lepiej powiedzieć, że została jedna czwarta (ćwiartka) pizzy, zamiast dwie ósme, prawda?
• Albo że zjedzono połowę ciasta, a nie trzy szóste.

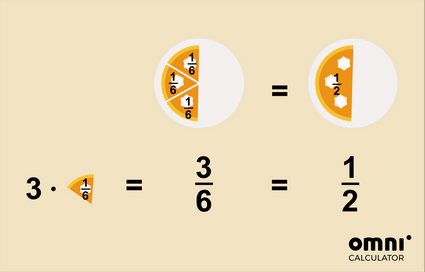
Aby uprościć ułamek, możesz użyć dwóch metod:

1. Zastosuj metodę brutalnej siły (brute force): podziel ułamek przez 2, 3, 5, 7, 11... aż do momentu, gdy dalsze dzielenie (bez reszty) będzie niemożliwe:

   ➽ ⁴²/₁₂₆ = /:2

   ➽ ²¹/₆₃ = /:3

   ➽ ⁷/₂₁ = /:7

   ➽ ¹/₃

2. Znajdź NWC — największy wspólny czynnik licznika i mianownika, a następnie podziel je przez tę liczbę: NWC(42,126) = 42, a więc:

   ➽ ⁴²/₁₂₆ = /:42

   ➽ ¹/₃

Przeczytaj więcej o skracaniu ułamków w naszym dedykowanym kalkulatorze skracania ułamków 🇺🇸. Zapoznaj się również z naszym niesamowitym kalkulator równoważników ułamków 🇺🇸, który może znaleźć wiele odpowiedników twojego ułamka.

Jeśli chcesz dowiedzieć się jak przeliczyć ułamek dziesiętny na ułamek zwykły, jesteś we właściwym miejscu. Tutaj znajdziesz przewodnik krok po kroku:

Załóżmy, że chcesz przeliczyć 0,32 na ułamek:

1. Potraktuj liczbę dziesiętną jako licznik. Wtedy mianownik będzie wynosił 1.

2. Przesuwaj przecinek w prawo, aż uzyskasz liczbę całkowitą:

   0,32 → 3,2 → 32

   Każde przesunięcie odpowiada mnożeniu przez 10

   0,32 ⋅ 10 → 3,2 ⋅ 10 → 32

3. Pomnożyłeś/aś licznik przez 10 ⋅ 10, a teraz musimy pomnożyć mianownik przez tę samą liczbę:

   1 ⋅ 10 ⋅ 10 = 100

4. Zamieniłeś/aś ułamek na liczbę dziesiętną! ✨ 0,32 → ³²/₁₀₀

5. Na koniec uprość wynik. Ponieważ największy wspólny czynnik dla 32 i 100 wynosi 4, podziel zarówno licznik, jak i mianownik przez tę wartość:

   ➽ ³²/₁₀₀ = ⁸/₂₅

I to wszystko, otrzymujesz ułamek w najprostszej postaci. ❤️

Cóż, najprostszym sposobem na zamianę ułamka na ułamek dziesiętny jest... użycie kalkulatora. Niezależnie od tego, czy jest to kalkulator ułamkowy, standardowy kalkulator kieszonkowy, czy nasze dedykowane narzędzie — przelicznik ułamków na ułamki dziesiętne 🇺🇸.

Czasami ułamek jest stosunkowo łatwy do zamiany na ułamek dziesiętny bez żadnych narzędzi — jak w przypadku 1/2, 3/4 (lub nawet 1/8). Wierzymy, że możesz dowiedzieć się, jak rozwinąć powyższe ułamki, aby mieć odpowiednio 10, 100, 1000 itd. w mianowniku:

• Pomnóż ¹/₂ przez 5, aby otrzymać 10 w mianowniku:

  ➽ ¹/₂ = ⁵/₁₀ = 0,5

• Pomnóż ³/₄ przez 25, aby otrzymać 100 w mianowniku:

  ➽ ³/₄ = ⁷⁵/₁₀₀ = 0,75

• Pomnóż ¹/₈ przez 125, aby otrzymać 1000 w mianowniku:

  ➽ ¹/₈ = ¹²⁵/₁₀₀₀ = 0,125

Ale co, jeśli nie masz przy sobie internetu ani kalkulatora, a jedynie długopis i papier? A twój ułamek nie wygląda na tak łatwy do rozwinięcia jak te powyżej? Wtedy prawdopodobnie będziesz musiał/a wykonać dzielenie do miejsc dziesiętnych ręcznie. Powodzenia! 🤞

Zanim to zrobisz, musisz znaleźć wspólny mianownik. Jako przykładu użyjemy ułamków 1/2 i 3/5. Wykonaj poniższe kroki, aby dodać ułamki o różnych mianownikach:

1. Znajdź najmniejszą wspólną wielokrotność (NWW) mianownika:

   10

2. Podziel NWW przez każdy mianownik i pomnóż liczniki przez wynik:

   • 10/2 = 5
     5 ⋅ 1 = 5

   • 10/5 = 2
     2 ⋅ 3 = 6

3. Dodaj liczby znalezione w kroku 2 i umieść odpowiedź nad NWW:

   • 6 + 5 = 11

   • 11/10 = 1 ¹/₁₀

4. Voila! Właśnie dodałeś/aś swoje ułamki.

Tak, każdy ułamek jest liczbą wymierną, ale nie wszystkie liczby wymierne są ułamkami. Liczba wymierna jest ułamkiem tylko wtedy, gdy licznik i mianownik są liczbami całkowitymi.

0,3333 zapisane jako ułamek to ³³³³/₁₀₀₀₀.

Aby znaleźć tę odpowiedź:

1. Zapisz liczbę dziesiętną jako licznik i 1 jako mianownik:

   0,3333/1

2. Przesuń kropkę dziesiętną w prawo na końcu liczby, aby pojawiła się jako liczba całkowita:

   3333

3. Dodaj taką samą liczbę zer do mianownika, jak liczba miejsc, o które przesunąłeś przecinek dziesiętny. W tym przypadku jest to cztery:

   10000

4. Umieść liczbę z kroku 2 jako licznik, a liczbę z kroku 3 jako mianownik:

   3333/10000

Iloczyn 1/2 i 5/3 wynosi 5/6.

Aby uzyskać tę odpowiedź, pomnóż liczniki i mianowniki w następujących krokach:

• 1 ⋅ 5 = 5

• 2 ⋅ 3 = 6

• 1/2 ⋅ 5/3 = 5/6