Kalkulator kątów w trójkącie

Kalkulator kąta trójkąta jest sprawdzonym rozwiązaniem, jeśli chcesz dowiedzieć się, jak wyznaczyć kąty trójkąta. Niezależnie od tego, czy masz podane trzy boki trójkąta, dwa boki i kąt, czy też dwa kąty, nasze narzędzie jest rozwiązaniem twoich problemów z geometrią.

Poniżej znajdziesz również wyjaśnienie podstawowych praw dotyczących kątów trójkąta: twierdzenie o sumie kątów trójkąta, twierdzenie o kącie zewnętrznym i twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie. Czytaj dalej, aby zrozumieć, jak działa kalkulator i wypróbuj go — wyliczanie brakujących kątów w trójkątach nigdy nie było łatwiejsze!

Istnieje kilka sposobów na wyliczenie kątów w trójkącie, w zależności od tego, co jest podane:

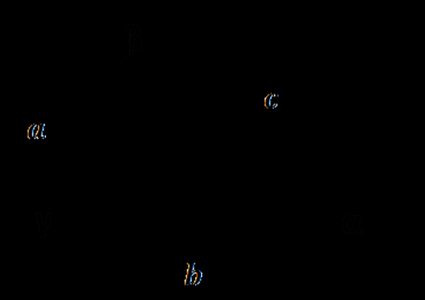
1. Dane trzy boki trójkąta

Użyj wzorów przekształconych z twierdzenia cosinusów:

Zatem:

Dla drugiego kąta mamy:

Zatem:

I trzeci kąt:

Zatem:

2. Dane są dwa boki trójkąta i jeden kąt

Jeśli kąt znajduje się pomiędzy podanymi bokami, możesz użyć twierdzenia cosinusów, aby znaleźć nieznany trzeci bok, a następnie użyć powyższych wzorów, aby znaleźć brakujące kąty, np. znając $a$,$b$,$γ$:

• oblicz $c = \sqrt{a^2 + b^2 - 2ab \cos(\gamma)}$;
• podstaw $c$ w $\alpha = \mathrm{arccos}\left(\frac{b^2 + c^2- a^2}{2bc}\right)$;
• następnie znajdź $\beta$ z twierdzenia o sumie kątów trójkąta: $\beta = 180\degree- \alpha - \gamma$

Jeśli kąt nie znajduje się pomiędzy podanymi bokami, możesz skorzystać z twierdzenia sinusów. Na przykład, załóżmy, że znamy $a$, $b$ i $\alpha$:

Zatem:

Jak wiesz, suma kątów w trójkącie jest równa $180\degree$. Na podstawie tego twierdzenia możemy znaleźć brakujący kąt: $\gamma = 180\degree- \alpha - \beta$

3. Dane dwa kąty

To najłatwiejsza opcja. Po prostu użyj twierdzenia o sumie kątów trójkąta, aby znaleźć brakujący kąt:

• $\alpha = 180\degree- \beta - \gamma$;
• $\beta= 180\degree- \alpha - \gamma$; oraz
• $\gamma = 180\degree- \alpha- \beta$.

We wszystkich trzech przypadkach możesz skorzystać z naszego kalkulatora kątów trójkąta — nie zawiedziesz się.

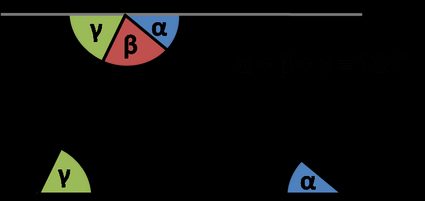
Twierdzenie to mówi, że kąty wewnętrzne trójkąta sumują się do $180\degree$:

Skąd to wiemy? Spójrz na rysunek: kąty oznaczone tymi samymi greckimi literami są przystające, ponieważ są kątami naprzemianległymi. Suma trzech kątów $\alpha$ $\beta$ , $\gamma$ jest równa $180\degree$, ponieważ pozwalają nam one uzyskać linię prostą. Ale to są przecież dokładnie trzy kąty wewnętrzne naszego trójkąta! Dlatego $\alpha + \beta+ \gamma = 180\degree$.

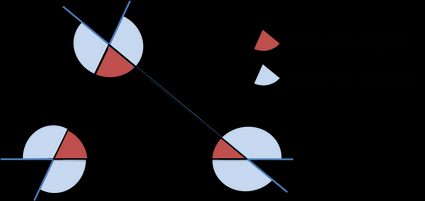
Kąt zewnętrzny trójkąta jest równy sumie przeciwległych kątów wewnętrznych.

• Każdy trójkąt ma sześć kątów zewnętrznych (dwa przy każdym wierzchołku są równej miary).
• Kąty zewnętrzne, wzięte po jednym w każdym wierzchołku, sumują się do $360\degree$.
• Kąt zewnętrzny jest uzupełnieniem sąsiedniego kąta wewnętrznego do kąta półpełnego.

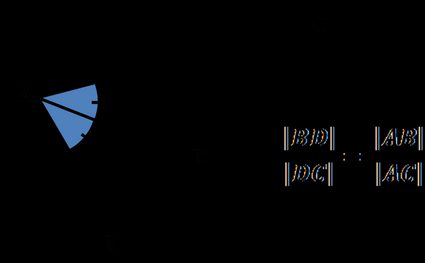
Twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie mówi, że

Dwusieczna kąta wewnętrznego trójkąta dzieli przeciwległy bok na dwa odcinki proporcjonalne do dwóch pozostałych boków trójkąta.

Lub, innymi słowy:

Stosunek długości $\overline{BD}$ do długości $\overline{DC}$ jest równy stosunkowi długości boku $\overline{AB}$ do długości boku $\overline{AC}$:

OK, przećwiczmy to, czego się właśnie nauczyliśmy. Załóżmy, że chcemy znaleźć brakujące kąty w naszym trójkącie. Jak to zrobić?

1. Znajdź wzory, których musisz użyć. W naszym przykładzie mamy podane dwa boki i jeden kąt. Wybierz opcję kąt i 2 boki.
2. Wpisz podane wartości. Na przykład wiemy, że $a = 9\ \mathrm{cm}$, $b = 14\ \mathrm{cm}$ i $\alpha = 30\degree$. Jeśli chcesz obliczyć to ręcznie, użyj twierdzenia sinusów:

Zatem:

• Z twierdzenia o sumie kątów w trójkącie wynika, że $\gamma = 180\degree- \alpha - \beta = 180\degree- 30\degree - 51,\!06\degree= 98,\!94\degree$

3. Kalkulator kątów trójkąta znajduje brakujące kąty w trójkącie. Są one równe tym, które obliczyliśmy ręcznie: $\beta = 51,\!06\degree$, $\gamma = 98,\!94\degree$; dodatkowo narzędzie wyznaczyło brakującą długość boku: $c = 17,\!78\ \mathrm{cm}$.

Rozumowanie podobne do tego, które zastosowaliśmy w tym kalkulatorze, pojawia się w innych obliczeniach trójkątów, na przykład w Kalkulatorze trójkątów kbk 🇺🇸 i kalkulatorze trójkątów bbk 🇺🇸!