Kalkulator kąta między wektorami

Z naszym kalkulatorem kąta między wektorami dowiesz się, jak wyznaczyć kąt między dwoma wektorami. Nie ma znaczenia, czy twoje wektory są na płaszczyźnie czy w przestrzeni trójwymiarowej, ani czy znasz ich współrzędne czy punkty końcowe — nasze narzędzie poradzi sobie w każdym przypadku. Poeksperymentuj z kalkulatorem i zajrzyj na wyjaśnienia poniżej: jeśli szukasz wzorów na kąt między dwoma wektorami, na pewno je tam znajdziesz.

W tej sekcji znajdziesz wzory na kąt między dwoma wektorami — i tylko wzory. Jeśli chcesz zrozumieć skąd one się biorą i jak je wyprowadzamy, przejdź bezpośrednio do następnego akapitu Jak znaleźć kąt między dwoma wektorami.

Kąt pomiędzy dwoma wektorami na płaszczyźnie

1. Wektory zadane przez współrzędne:

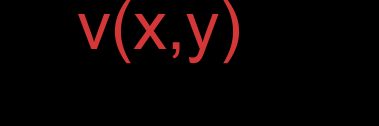
Mamy dany wektor $\boldsymbol a$:

oraz wektor $\boldsymbol b$:

Kąt $\alpha$ między nimi wynosi:

2. Wektory zadane punktem początkowym i końcowym:

Dla wektora $\boldsymbol a$ mamy punkt początkowy:

oraz punkt końcowy:

Zatem wektor $a$ ma współrzędne:

Wektor $b$ ma punkt początkowy:

oraz punkt końcowy:

więc $\boldsymbol b$ ma współrzędne:

Zatem kąt $\alpha$ między tymi wektorami wyliczymy następująco:

Kąt pomiędzy dwoma wektorami w 3D.

1. Wektory reprezentowane przez współrzędne:

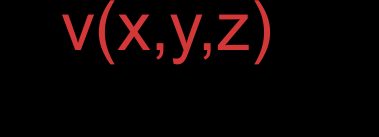
oraz

Wówczas wzór na kąt $\alpha$ między wektorami ma postać:

2. Wektory zadane punktem początkowym i końcowym:

Punkt początkowy wektora $\boldsymbol{a}$:

oraz jego punkt końcowy:

Zatem $\boldsymbol{a}$ ma współrzędne:

Punkt początkowy wektora $\boldsymbol{b}$:

oraz jego punkt końcowy:

Zatem $\boldsymbol{b}$ ma współrzędne:

Znajdujemy wzór końcowy na kąt $\alpha$ analogicznie jak w przypadku dwuwymiarowym:

Możliwe jest również, aby jeden kąt był zdefiniowany przez współrzędne, a drugi przez punkt początkowy i końcowy, ale nie pozwolimy, aby to jeszcze bardziej zaciemniło ten rozdział. Ważne jest tylko to, że nasz kalkulator kąta między dwoma wektorami ma wszystkie możliwe kombinacje, które są dostępne dla ciebie na wyciągnięcie ręki.

OK, powyższy akapit był trochę skrótowy (TL;DR). Aby lepiej zrozumieć wzory na kąt między wektorami, zobaczmy teraz jak je wyprowadzić:

1. Zaczynamy od podstawowego wzoru na obliczenie iloczynu skalarnego 🇺🇸:

   Iloczyn skalarny definiujemy jako iloczyn długości (modułów) wektorów pomnożony przez cosinus kąta między nimi (tutaj oznaczany przez $\alpha$):

2. Przekształcamy równanie, dzieląc obie strony przez iloczyn długości wektorów:

Znajdujemy $\alpha$, obliczając arc cos obu stron:

3. Teraz musimy zapoznać się z definicją długości wektora:

   Ponieważ długość wektora jest pierwiastkiem kwadratowym z sumy kwadratów jego składowych, otrzymujemy:

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2}$ na płaszczyźnie; oraz.

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2+z^2}$ w przestrzeni trójwymiarowej.

Zauważ, że ten sam wzór pojawia się w kalkulatorze odległości. Pochodzi on bezpośrednio z geometrii — możesz go wyprowadzić za pomocą kalkulatora twierdzenia Pitagorasa.

4. Skorzystamy następnie ze wzoru iloczyn skalarny (mówiącego, że jest on sumą iloczynów składowych wektorów) i podstawimy długości:

Na płaszczyźnie:

Przyjmijmy, że wektory $\boldsymbol{a}$ i $\boldsymbol{b}$ mają współrzędne:

oraz

W przestrzeni 3D:

Jeśli wektory $\boldsymbol{a}$ i $\boldsymbol{b}$ mają współrzędne:

oraz

to

I to wszystko!

Jeśli twoje wektory mają inną postać (znasz ich punkty początkowe i końcowe), musisz wcześniej wykonać pewne obliczenia. Celem jest sprowadzenie ich do standardowej postaci.

Na przykład, jeśli twój wektor jest opisany przez punkt początkowy $A=(x_1, y_1)$ i punkt końcowy $B=(x_2, y_2)$, to wektor może być wyrażony jako:

Rozwiążemy teraz kilka przykładowych zadań, aby rozwiać twoje ostatnie wątpliwości.

Załóżmy, że chcemy znaleźć kąt między dwoma wektorami:

oraz $\boldsymbol{b}$, który jest wektorem z punktem początkowym $A = (1, 1, 2)$ i punktem końcowym $B = (-4, -8, 6)$.

Co musimy zrobić?

1. Najpierw obliczamy współrzędne wektora $\boldsymbol{b}$, biorąc pod uwagę punkt początkowy i końcowy:

2. Następnie znajdujemy iloczyn skalarny wektorów $\boldsymbol{a}$ i $\boldsymbol{b}$:

3. Następnie wyznaczamy długości wektorów:

oraz

4. Na koniec wykorzystamy przekształcone równanie iloczynu skalarnego:

I już! Właśnie obliczyliśmy kąt pomiędzy dwoma wektorami w przestrzeni trójwymiarowej. Gratulacje!

Jeśli chcesz poznać więcej ciekawych pojęć, polecamy sprawdzić kalkulator średniej szybkości zmian 🇺🇸.

Jak działa nasz kalkulator kąta między dwoma wektorami? Postępuj zgodnie z poniższą instrukcją:

1. Wybierz przestrzeń: 2D lub 3D. Rozważmy ten sam przykład, co w poprzedniej sekcji. Nasze wektory i punkty mają trzy współrzędne, więc musimy wybrać opcję 3D.

2. Wybierz reprezentację pierwszego wektora. Dla pierwszego wektora mamy podane współrzędne, więc zostawiamy wartość domyślną: współrzędne.

3. Wprowadzamy pierwszy wektor. Wpisz $x = 3$, $y = 6$, $z = 1$.

4. Wybieramy reprezentację drugiego wektora. Tym razem musimy zmienić ją na punkty.

5. Wprowadzamy dane dotyczące drugiego wektora. Wpisz $\boldsymbol A = (1,1,2)$ oraz $\boldsymbol B = (-4,-8,6)$ w odpowiednie pola.

6. Nasz kalkulator znalazł kąt pomiędzy tymi wektorami w momencie, gdy ostatnie pole zostało uzupełnione. W naszym przykładzie otrzymaliśmy $150,\!2\degree$, co jest oczywiście tym samym wynikiem, który otrzymaliśmy z ręcznych obliczeń.

Wektor to obiekt geometryczny, który ma zarówno wielkość, jak i kierunek. Bardzo często używamy wektorów do reprezentowania wielkości fizycznych, takich jak siła, prędkość czy przemieszczenie.

Kąt między dwoma wektorami definiuje się jako arcus cosinus ze stosunku iloczynu skalarnego tych wektorów do iloczynu ich długości.

Aby obliczyć kąt między dwoma wektorami w przestrzeni dwuwymiarowej, musisz:

1. Obliczyć iloczyn skalarny tych wektorów.
2. Podzielić iloczyn skalarny przez długość pierwszego wektora.
3. Podzielić wynik przez długość drugiego wektora.

Matematycznie, kąt α między dwoma wektorami [x_a,y_a] i [x_b, y_b] można zapisać jako:

α = arccos[(x_a x_b + y_a y_b) / (√(x_a² + y_a²) × √(x_b² + y_b²))]

Aby obliczyć kąt między dwoma wektorami w przestrzeni 3D:

1. Oblicz iloczyn skalarny tych wektorów.
2. Podziel ten iloczyn skalarny przez długość pierwszego wektora.
3. Podziel wynik przez długość drugiego wektora.

Matematycznie, kąt α między wektorami [x_a,y_a,z_a] i [x_b, y_b,z_b] można zapisać jako:

α = arccos[(x_a x_b + y_a y_b + z_a z_b) / (√(x_a² + y_a² + z_a²) × √(x_b² + y_b² + z_b²) )]