Kalkulator symbolu Newtona

Witamy w kalkulatorze symbolu Newtona, gdzie będziesz mieć okazję obliczyć i dowiedzieć się wszystkiego o tajemniczej formule n po k. Wyrażenie to oznacza liczbę kombinacji wyboru k ze zbioru n elementów i odpowiada przyciskowi nCr na prawdziwym kalkulatorze.

Aby uzyskać odpowiedź na pytanie „Co to jest dwumian?”, dowiedzieć się czym są kombinacje, rozwiązać symbol Newtona „4 po 2” i wiele więcej, zapoznaj się z dalszą częścią artykułu.

W matematyce (a dokładniej w algebrze), dwumian to wielomian z dwoma wyrazami (stąd nazwa). Na przykład wyrażenia x + 1, xy - 2ab lub x³z - 0,5y⁵ są dwumianami, ale x⁵, a + b - cd lub x² - 4x² już nie (ostatnie ma dwa wyrazy, ale możemy uprościć to wyrażenie do -3x², które ma tylko jeden).

Teraz gdy wiemy już, czym jest dwumian, przyjrzyjmy się bliżej podnoszeniu go do pewnej potęgi:

(x² - 3)³

Istnieją odmiany tego wyrażenia — wzory skróconego mnożenia, które możesz znać ze szkoły:

(a + b)² = a² + 2ab + b²

(a - b)² = a² - 2ab + b²

Wielomian, który otrzymamy po prawej stronie, nazywany jest wzorem dwumianowym tego, co mieliśmy w nawiasach. Możesz wierzyć lub nie, ale możemy znaleźć te wyrażenia dla dowolnej dodatniej potęgi będącej liczbą całkowitą. Poniższy wzór przedstawia rozwinięcie tego wyrażenia:

gdzie:

• $C_k$ jest liczbą wszystkich możliwych kombinacji $k$ ze zbioru liczącego $n$ elementów.

Ponadto, dla danego n, liczby te są zgrabnie przedstawione dla kolejnych wartości n w wierszach tak zwanego trójkąta Pascala, gdzie pojedynczy wiersz jako całość zlicza wszystkie możliwe kombinacje. Odwiedź nasz kalkulator trójkąta Pascala 🇺🇸, aby wygenerować trójkąt Pascala o wybranym rozmiarze.

To dobry moment, abyśmy dowiedzieli się, czym właściwie są kombinacje w ujęciu matematycznym.

Wyobraź sobie, że jesteś studentem i ucinasz sobie drzemkę podczas wykładu. Nagle nauczyciel sprowadza cię z powrotem na ziemię, mówiąc: „A teraz rozlosujemy członków grup, w których wykonają państwo projekty zaliczeniowe.” Wygląda na to, że jednak będziesz musiał trochę popracować.

Problem polega na tym, że jest tylko jeden kolega, z którym chciałbyś pracować nad projektem. Jeśli w grupie jest dwadzieścia osób, a nauczyciel podzieli wszystkich na czteroosobowe grupy, to jakie jest prawdopodobieństwo, że będziesz w drużynie ze swoim przyjacielem?

Każda możliwa grupa jest przykładem kombinacji. W tym przypadku jest to kombinacja czterech elementów ze zbioru dwudziestu elementów, czyli czterech uczniów z dwudziestoosobowej grupy. Najważniejsze jest to, że kolejność wybranych elementów nie ma znaczenia. W końcu wszyscy członkowie zespołu projektowego są równi (z wyjątkiem tych, którzy nie wykonują żadnej pracy).

Liczba kombinacji k elementów ze zbioru n elementów prezentuje się następująco:

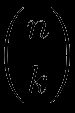
(jak ułamek n przez k, ale bez poziomej kreski), który czytamy jako „n po k”. Jest to również symbol, który pojawia się gdy wybieramy nCr na kalkulatorze (nie na naszym kalkulatorze symbolu Newtona, lecz na zwykłym, prawdziwym kalkulatorze). Na przykład,

czytamy jako „4 po 2”, oraz

czytamy jako „6 po 2”. W niektórych podręcznikach dwumian Newtona jest również oznaczany jako C(n,k), co czyni go funkcją n i k. „A jak to obliczyć?” Cóż, dość łatwo. Wzór na n po k to

n! / (k! ⋅ (n - k)!)

gdzie wykrzyknik oznacza silnię liczby naturalnej n.

n! = 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ n

Oznacza to, że, na przykład, 4 po 2 to:

4! / (2! ⋅ (4 - 2)!) = (1 ⋅ 2 ⋅ 3 ⋅ 4) / (1 ⋅ 2 ⋅ 1 ⋅ 2) = 6

a 6 po 2 to

6! / (2! ⋅ (6 - 2)!) = (1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6) / (1 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 3 ⋅ 4) = 15

Aby dowiedzieć się więcej na ten temat, odwiedź nasz kalkulator silni 🇺🇸!

Możemy więc wybrać dwa elementy ze zbioru czterech na sześć różnych sposobów, a ze zbioru sześciu na piętnaście sposobów.

Zanim przejdziemy dalej, spójrzmy jeszcze raz na formułę n po k. Możemy uzyskać z niej całkiem interesującą własność symetryczną.

Jeśli weźmiemy n po n - k, to otrzymamy:

n! / ((n - k)! ⋅ (n - (n - k))!) = n! / ((n - k)! ⋅ k!)

co jest tym samym, co n po k (ponieważ mnożenie jest przemienne). Innymi słowy, mamy:

lub C(n,k) = C(n,n-k) w innej notacji.

W poprzednim rozdziale opisaliśmy czym jest silnia. W kombinatoryce oznacza liczbę permutacji. Permutacja n oznacza ułożenie n elementów w pewnej kolejności. Na przykład, jeśli mamy trzy słodkie buźki kotka; 😹, 😻 i 🙀, to możemy je uporządkować na sześć różnych sposobów:

(😹, 😻, 🙀)

(😹, 🙀, 😻)

(😻, 😹, 🙀)

(😻, 🙀, 😹)

(🙀, 😹, 😻)

(🙀, 😻, 😹)

Zauważ, że zgadza się to z tym, co mówi nam silnia:

3! = 3 ⋅ 2 ⋅ 1 = 6

Odwiedź nasz kalkulator permutacji 🇺🇸, aby dowiedzieć się więcej na ten temat.

Zauważ, że możemy również zrozumieć ten wzór w następujący sposób: wybieramy pierwszy element z trzech (3 opcje), drugi z dwóch pozostałych (ponieważ już wybraliśmy jedną), a trzeci z jednego, który pozostał (ponieważ już wybraliśmy dwie). Mnożymy liczbę wyborów: 3 ⋅ 2 ⋅ 1 = 6 i otrzymujemy czynnik.

Kiedy porównujemy permutację z kombinacją, słowem kluczowym jest kolejność. Jak powiedzieliśmy w poprzedniej sekcji, znaczenie kombinacji to wybranie kilku elementów z większego zbioru. Zasadniczo mówimy, które z nich wybieramy, ale nie który jest pierwszy, drugi itd. Tworzą one zbiór jako całość.

Permutacja jednak umieszcza elementy w ustalonej kolejności, powstaje swego rodzaju sekwencja. Co więcej, permutacja używa wszystkich elementów ze zbioru, który mamy, podczas gdy kombinacja wybiera tylko niektóre z nich.

Jako przykład, ponownie postaw się w sytuacji studenta. Kiedy nauczyciel wybrał grupę za niego. Nauczyciel wybrał kombinację wybranych uczniów. A kiedy przychodzi czas na prezentację twojego projektu i zadają każdemu z was po jednym pytaniu, wówczas mamy do czynienia z permutacją (określając kolejność, w jakiej zadają wam pytania). A wszyscy wiemy, jak ważna może być kolejność odpytywanie, dla twojej oceny końcowej.

Dwumian Newtona, czyli współczynniki dwumianowe, to jeden z najważniejszych ciągów liczbowych w matematyce i kombinatoryce. Pojawia się bardzo często w statystyce i obliczeniach prawdopodobieństwa, oraz w rozkładzie dwumianowym (również w ujemnym rozkładzie dwumianowym 🇺🇸). Czy to oznacza, że tylko maniacy matematyki mają z nich prawdziwy pożytek?

Wcale nie! Każda gra hazardowa opiera się na przypadku, a współczynniki dwumianowe są ich istotnym elementem. Prosty rzut monetą jest najprostszym przykładem, który możesz obliczyć za pomocą naszego kalkulatora prawdopodobieństwa rzutu monetą. Pójdźmy jednak o krok dalej i przyjrzyjmy się pokerowi.

Czy kiedykolwiek pojawiło się w twojej głowie pytanie, dlaczego niektóre układy w pokerze są bardziej wartościowe niż inne? Po prostu dlatego, że ich wystąpienie jest mniej prawdopodobne (chyba że ktoś oszukuje, ale widzieliśmy wystarczająco dużo gangsterskich seriali telewizyjnych, aby wiedzieć, że to zazwyczaj zły pomysł).

W zwykłej talii znajdują się 52 karty, a w Texas Hold'em gracz otrzymuje pięć kart. Nasz kalkulator współczynnika dwumianowego i formuła n po k (w naszym przypadku z n = 52 i k = 5) mówi nam, że przekłada się to na 2 598 960 możliwych rozdań w grze w pokera. Całkiem sporo, nie sądzisz? A teraz rozważ prawdopodobieństwo wystąpienia najlepszego możliwego układu — pokera królewskiego w kierach (as, król, dama, walet i 10). Ten układ może się zdarzyć tylko w jednym przypadku — gdy otrzymamy dokładnie te karty. Oznacza to, że jest to szansa 1 na 2 598 960. Nie zalecamy stawiania wszystkich swoich oszczędności na takie szanse.

Weźmy inny przykład — full (trójka i para). Tym razem jest znacznie bardziej prawdopodobne. W końcu każda z 13 kart w kolorze może być trójką, a para znajduje się w jednej z pozostałych 12 kart (nie może mieć tej samej wartości co trójka). Co więcej, trójka występuje tylko w trzech z czterech symboli kart, a para tylko w dwóch.

I to jest moment, w którym przypominamy sobie znaczenie kombinacji! Musimy wybrać trzy z czterech symboli dla trójki i kombinację dwóch z czterech dla pary. Formuła n po k przekłada to na 4 po 3 i 4 po 2, a kalkulator symbolu Newtona liczy je odpowiednio jako 4 i 6. Podsumowując, jeśli teraz pomnożymy otrzymane liczby, okaże się, że jest

13 ⋅ 12 ⋅ 4 ⋅ 6 = 3744

możliwych układów, które dają fulla. Cóż, nie jest to zbyt wiele w porównaniu do wszystkich możliwości, ale przynajmniej jest to 3744 razy bardziej prawdopodobne niż poker królewski w kierach.

Mimo to sugerujemy regularne oszczędzanie pieniędzy jako lepszą technikę inwestycyjną niż hazard.