Kalkulator rozkładu na czynniki

Za pomocą tego kalkulatora czynników wyznaczysz czynniki dowolnej dodatniej liczby naturalnej. Czynnik to dzielnik (liczba całkowita), który dzieli daną liczbę do postaci całkowitej.

Wprowadź dowolną dodatnią liczbę całkowitą, a w mgnieniu oka znajdziesz wszystkie dodatnie czynniki tej liczby. Jeśli nie wiesz, czym jest czynnik, przewiń w dół, aby znaleźć definicję czynnika. Znajdziesz tu także zasady podzielności z osobnym akapitem poświęconym mało znanej zasadzie podzielności przez 7.

Czynnik, zwany również dzielnikiem (ang. factor), to dowolna liczba, która dzieli się równo na inną liczbę. Innymi słowy, czynnikami są liczby, które możemy pomnożyć razem, aby otrzymać określony iloczyn:

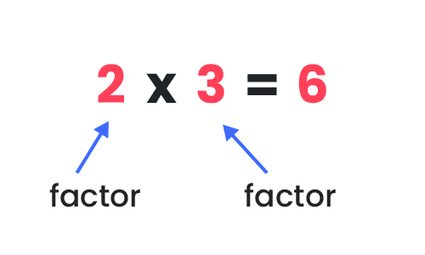
Możemy zauważyć, że dzielenie iloczynu przez jego czynnik nie pozostawia reszty.

Definicja czynnika nie jest ujednolicona: niektóre wersje twierdzą, że czynnik może być zarówno ujemny, jak i dodatni, ale w innych przypadkach termin ten jest ograniczony tylko do czynników dodatnich.
Na przykład, czynnikami liczby 8 są liczby 1, 2, 4 i 8. Ale z drugiej strony, jeśli pomnożysz -2 razy -4, otrzymasz również 8; dlatego -2 i -4 są czynnikami 8 zgodnie z pierwszą definicją.

Technicznie rzecz biorąc, możesz mieć ujemne czynniki, choć ich używanie nie jest tak popularne. Dla celów praktycznych nasz kalkulator rozkładu na czynniki znajduje tylko czynniki dodatnie. Jeśli z jakiegoś powodu potrzebujesz ujemnych, po prostu dodaj minus przed każdą uzyskaną wartością:

Czynniki liczby 8 to: 1, 2, 4, 8

oraz -1, -2, -4, -8.

Istnieje wiele reguł podzielności, które znacznie ułatwiają ręczne znajdowanie czynników. Najczęściej używane z nich to:

• 2: Każda liczba parzysta jest podzielna przez 2.

• 3: Liczba jest podzielna przez 3, jeśli suma cyfr w liczbie jest podzielna przez 3.

• 4: Liczba jest podzielna przez 4, jeśli dwie ostatnie cyfry tworzą liczbę podzielną przez 4.

• 5: Każda liczba kończąca się na 5 lub 0 jest podzielna przez 5.

• 6: Liczba jest podzielna przez 6, jeśli jest podzielna przez 2 i 3.

• 7: Reguła podzielności przez 7 również istnieje, ale jest nieco bardziej skomplikowana. Sprawdź nasz krótki paragraf poniżej.

• 8: Jeśli ostatnie trzy cyfry tworzą liczbę, która jest podzielna przez 8, to cała liczba jest podzielna przez 8.

• 9: Jeśli suma cyfr tworzących liczbę jest podzielna przez 9, to cała liczba jest podzielna przez 9.

• 10: Każda liczba kończąca się na 0 jest podzielna przez 10.

Istnieje wiele aspektów matematyki, w których ważna jest umiejętność znajdowania czynników. Kalkulator czynników pomaga znaleźć największy wspólny dzielnik, najmniejszą wspólną wielokrotność i czynniki pierwsze.

Chcesz sprawdzić, czy 7 jest czynnikiem naszej liczby? Istnieją dwie podstawowe metody sprawdzenia tego. Pokażemy to na przykładzie liczby 13 468.

1. Metoda 1
   1. Weź ostatnią cyfrę. W naszym przypadku jest to 8.
   2. Podwój ostatnią cyfrę. 2 ⋅ 8 = 16.
   3. Weź pozostałe cyfry (obcięta liczba). Dla nas jest to 1346.
   4. Znajdź różnicę między liczbą z pozostałych cyfr a podwojoną ostatnią cyfrą. To oznacza, że musimy odjąć 16 od 1346. 1346 - 16 = 1330.
   5. Kontynuuj tę procedurę, aż uzyskasz liczbę, o której wiadomo, że jest podzielna przez 7 (lub nie). Nie wiemy od razu, czy 1330 jest podzielne przez 7, więc powtarzamy kroki od nowa:

   • 0;

   • 2 ⋅ 0 = 0;

   • 133;

   • 133 - 0 = 133.

     Czy liczba 133 jest podzielna przez 7? Nie jest to jeszcze widoczne, więc powtarzamy procedurę jeszcze raz:

   • 3;

   • 2 ⋅ 3 = 6;

   • 13;

   • 13 - 6 = 7.

Świetnie! Uzyskaliśmy liczbę podzielną przez 7, więc to oznacza, że nasza oryginalna liczba, 13 468 jest również podzielna przez 7.

2. Metoda 2

   1. Weź cyfry liczby w odwrotnej kolejności. Tak więc dla naszej oryginalnej liczby 13 468, mamy 8 6 4 3 1.

   2. Pomnóż je kolejno przez cyfry 1, 3, 2, 6, 4, 5. Powtórz lub skróć ten ciąg do potrzebnej długości. W naszym przypadku otrzymamy:

      8 ⋅ 1, 6 ⋅ 3, 4 ⋅ 2, 3 ⋅ 6 i 1 ⋅ 4.

   3. Dodaj otrzymane iloczyny. Jeśli otrzymany wynik jest podzielny przez 7, to oryginalna liczba również jest podzielna:

      (8 × 1) + (6 × 3) + (4 × 2) + (3 × 6) + (1 × 4) = 8 + 18 + 8 + 18 + 4 = 56, co jest liczbą podzielną przez 7.

Rozkład na czynniki pierwsze jest rozszerzeniem rozkładu na czynniki, w którym wszystkie czynniki są liczbami pierwszymi. Na przykład, załóżmy, że chcemy uzyskać czynniki pierwsze liczby 48. Czynniki 48 to 1, 2, 3, 4, 6, 8, 12, 16, 24, 48. Zauważ, że nie są to wszystkie liczby pierwsze, więc musimy rozłożyć je na czynniki pierwsze. Po zakończeniu procesu otrzymujemy 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3. Chociaż 1 jest czynnikiem, wielu matematyków nie uważa 1 za liczbę pierwszą. Kalkulator rozkładu na czynniki pierwsze 🇺🇸 jest przydatnym narzędziem do uzyskiwania tych wartości.

Innym polem zainteresowania jest obliczanie największego wspólnego dzielnika (NWD) zbioru liczb. Aby to zrobić, otrzymujemy czynnik pierwszy wszystkich liczb. Następnie mnożymy wszystkie czynniki, które są takie same w każdym zbiorze. Na przykład, załóżmy, że chcemy uzyskać NWD liczb 24, 44 i 68. Czynniki pierwsze to 24 = 2 ⋅ 2 ⋅ 2 ⋅ 3, 44 = 2 ⋅ 2 ⋅ 11 i 68 = 2 ⋅ 2 ⋅ 17. Zauważ, że jedyną liczbą występującą we wszystkich zbiorach czynników jest 2, która występuje dwukrotnie, więc NWD wynosi 2 ⋅ 2 = 4. Kalkulator największego wspólnego dzielnika w prosty i szybki sposób obliczy ten wynik.

Ściśle związana z NWD jest najmniejsza wspólna wielokrotność, w skrócie NWW. Proces wygląda następująco: otrzymujemy czynniki pierwsze i mnożymy najwyższą potęgę wszystkich obecnych czynników. W powyższym przykładzie, NWW wynosiłoby 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 11 ⋅ 17 = 4488. Korzystanie z kalkulatora najmniejszej wspólnej wielokrotności 🇺🇸 znacznie ułatwi ten żmudny proces.

Podczas gdy uczymy się arytmetyki, sprawdź nasz kalkulator rozdzielności działań 🇺🇸, aby dowiedzieć się, jak radzić sobie ze złożonymi wyrażeniami matematycznymi.

Możesz użyć kalkulatora czynników, aby uzyskać poniższą listę czynników:

• Czynniki 1: 1;

• Czynniki 2: 1, 2;

• Czynniki 3: 1, 3;

• Czynniki 4: 1, 2, 4;

• Czynniki 5: 1, 5;

• Czynniki z 6: 1, 2, 3, 6;

• Czynniki z 7: 1, 7;

• Czynniki z 8: 1, 2, 4, 8;

• Czynniki z 9: 1, 3, 9;

• Czynniki 10: 1, 2, 5, 10;

• Czynniki 11: 1, 11;

• Czynniki 12: 1, 2, 3, 4, 6, 12;

• Czynniki z 13: 1, 13;

• Czynniki z 14: 1, 2, 7, 14;

• Czynniki z 15: 1, 3, 5, 15;

• Czynniki z 16: 1, 2, 4, 8, 16;

• Czynniki 17: 1, 17;

• Czynniki z 18: 1, 2, 3, 6, 9, 18;

• Czynniki z 19: 1, 19;

• Czynniki z 20: 1, 2, 4, 5, 10, 20;

• Czynniki 21: 1, 3, 7, 21;

• Czynniki z 22: 1, 2, 11, 22;

• Czynniki 23: 1, 23;

• Czynniki z 24: 1, 2, 3, 4, 6, 8, 12, 24;

• Czynniki 25: 1, 5, 25;

• Czynniki z 26: 1, 2, 13, 26;

• Czynniki z 27: 1, 3, 9, 27;

• Czynniki z 28: 1, 2, 4, 7, 14, 28;

• Czynniki z 29: 1, 29;

• Czynniki z 30: 1, 2, 3, 5, 6, 10, 15, 30;

• Czynniki 31: 1, 31;

• Czynniki z 32: 1, 2, 4, 8, 16, 32;

• Czynniki 33: 1, 3, 11, 33;

• Czynniki 34: 1, 2, 17, 34;

• Czynniki z 35: 1, 5, 7, 35;

• Czynniki z 36: 1, 2, 3, 4, 6, 9, 12, 18, 36;

• Czynniki 37: 1, 37;

• Czynniki 38: 1, 2, 19, 38;

• Czynniki 39: 1, 3, 13, 39;

• Czynniki z 40: 1, 2, 4, 5, 8, 10, 20, 40;

• Czynniki 41: 1, 41;

• Czynniki z 42: 1, 2, 3, 6, 7, 14, 21, 42;

• Czynniki 43: 1, 43;

• Czynniki 44: 1, 2, 4, 11, 22, 44;

• Czynniki 45: 1, 3, 5, 9, 15, 45;

• Czynniki 46: 1, 2, 23, 46;

• Czynniki 47: 1, 47;

• Czynniki z 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48;

• Czynniki 49: 1, 7, 49;

• Czynniki z 50: 1, 2, 5, 10, 25, 50;

• Czynniki 51: 1, 3, 17, 51;

• Czynniki z 52: 1, 2, 4, 13, 26, 52;

• Czynniki 53: 1, 53;

• Czynniki z 54: 1, 2, 3, 6, 9, 18, 27, 54;

• Czynniki z 55: 1, 5, 11, 55;

• Czynniki z 56: 1, 2, 4, 7, 8, 14, 28, 56;

• Czynniki z 57: 1, 3, 19, 57;

• Czynniki 58: 1, 2, 29, 58;

• Czynniki z 59: 1, 59;

• Czynniki z 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60;

• Czynniki 61: 1, 61;

• Czynniki z 62: 1, 2, 31, 62;

• Czynniki z 63: 1, 3, 7, 9, 21, 63;

• Czynniki z 64: 1, 2, 4, 8, 16, 32, 64;

• Czynniki z 65: 1, 5, 13, 65;

• Czynniki z 66: 1, 2, 3, 6, 11, 22, 33, 66;

• Czynniki z 67: 1, 67;

• Czynniki z 68: 1, 2, 4, 17, 34, 68;

• Czynniki z 69: 1, 3, 23, 69;

• Czynniki z 70: 1, 2, 5, 7, 10, 14, 35, 70;

• Czynniki z 71: 1, 71;

• Czynniki z 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72;

• Czynniki z 73: 1, 73;

• Czynniki z 74: 1, 2, 37, 74;

• Czynniki z 75: 1, 3, 5, 15, 25, 75;

• Czynniki z 76: 1, 2, 4, 19, 38, 76;

• Czynniki z 77: 1, 7, 11, 77;

• Czynniki z 78: 1, 2, 3, 6, 13, 26, 39, 78;

• Czynniki z 79: 1, 79;

• Czynniki z 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80;

• Czynniki z 81: 1, 3, 9, 27, 81;

• Czynniki z 82: 1, 2, 41, 82;

• Czynniki z 83: 1, 83;

• Czynniki z 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84;

• Czynniki z 85: 1, 5, 17, 85;

• Czynniki 86: 1, 2, 43, 86;

• Czynniki z 87: 1, 3, 29, 87;

• Czynniki z 88: 1, 2, 4, 8, 11, 22, 44, 88;

• Czynniki z 89: 1, 89;

• Czynniki z 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90;

• Czynniki 91: 1, 7, 13, 91;

• Czynniki z 92: 1, 2, 4, 23, 46, 92;

• Czynniki z 93: 1, 3, 31, 93;

• Czynniki z 94: 1, 2, 47, 94;

• Czynniki z 95: 1, 5, 19, 95;

• Czynniki z 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96;

• Czynniki z 97: 1, 97;

• Czynniki z 98: 1, 2, 7, 14, 49, 98;

• Czynniki z 99: 1, 3, 9, 11, 33, 99;

• Czynniki z 100: 1, 2, 4, 5, 10, 20, 25, 50, 100;

• Czynniki 104: 1, 2, 4, 8, 13, 26, 52, 104;

• Czynniki z 105: 1, 3, 5, 7, 15, 21, 35, 105;

• Czynniki z 108: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108;

• Czynniki 110: 1, 2, 5, 10, 11, 22, 55, 110;

• Czynniki 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, 112;

• Czynniki z 117: 1, 3, 9, 13, 39, 117;

• Czynniki 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120;

• Czynniki 121: 1, 11, 121;

• Czynniki 125: 1, 5, 25, 125;

• Czynniki z 126: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126;

• Czynniki 130: 1, 2, 5, 10, 13, 26, 65, 130;

• Czynniki z 132: 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132;

• Czynniki 135: 1, 3, 5, 9, 15, 27, 45, 135;

• Czynniki 140: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140;

• Czynniki 144: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144;

• Czynniki 147: 1, 3, 7, 21, 49, 147;

• Czynniki 150: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150;

• Czynniki 162: 1, 2, 3, 6, 9, 18, 27, 54, 81, 162;

• Czynniki 169: 1, 13, 169;

• Czynniki 175: 1, 5, 7, 25, 35, 175;

• Czynniki z 180: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180;

• Czynniki 189: 1, 3, 7, 9, 21, 27, 63, 189;

• Czynniki z 192: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192;

• Czynniki 196: 1, 2, 4, 7, 14, 28, 49, 98, 196;

• Czynniki 200: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200;

• Czynniki 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210;

• Czynniki 216: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216;

• Czynniki 225: 1, 3, 5, 9, 15, 25, 45, 75, 225;

• Czynniki 240: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240;

• Czynniki 245: 1, 5, 7, 35, 49, 245;

• Czynniki 250: 1, 2, 5, 10, 25, 50, 125, 250;

• Czynniki z 256: 1, 2, 4, 8, 16, 32, 64, 128, 256;

• Czynniki 270: 1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270;

• Czynniki 288: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288;

• Czynniki 294: 1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, 294;

• Czynniki 300: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300;

• Czynniki 343: 1, 7, 49, 343;

• Czynniki 360: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360;

• Czynniki 375: 1, 3, 5, 15, 25, 75, 125, 375;

• Czynniki 400: 1, 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 200, 400;

• Czynniki 500: 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, 500; oraz

• Czynniki 625: 1, 5, 25, 125, 625.

1. Rozłóż wielomian na jego czynniki pierwsze. Dotyczy to również symboli algebraicznych.
2. Znajdź czynniki występujące w każdym wyrażeniu, zarówno w liczbach, jak i symbolach.
3. Przenieś te czynniki poza nawiasy.
4. Uprość, aby ostatecznie otrzymać czynnik wielomianu.

Rozkład na czynniki pierwsze to po prostu rozkład na czynniki, w którym ograniczamy się do zawarcia w zbiorze jedynie liczb pierwszych. Pamiętaj, że 1 nie jest uważana za liczbę pierwszą.

Wspólny czynnik to czynnik, który dzielą dwie liczby. Na przykład, 4 i 6 mają wspólny czynnik równy 2. Liczby mogą mieć wiele wspólnych czynników, a ich znalezienie jest ważnym krokiem w znalezieniu największego wspólnego dzielnika.

Pary czynników to dwie liczby, które po pomnożeniu dają w wyniku określoną liczbę. Zazwyczaj są one podawane jako zbiór par czynników dla danej liczby, czyli wszystkich par liczb, które po pomnożeniu razem dają tę samą liczbę.