Kalkulator kąta środkowego

Czy kiedykolwiek zastanawiałeś/aś się, jak znaleźć kąt środkowy koła? Nasz kalkulator kąta środkowego ci w tym pomoże; jedyne zmienne, których potrzebujesz, to długość łuku i promień.

Czytaj dalej, aby poznać definicję kąta środkowego i dowiedzieć się, jak używać wzoru na kąt środkowy.

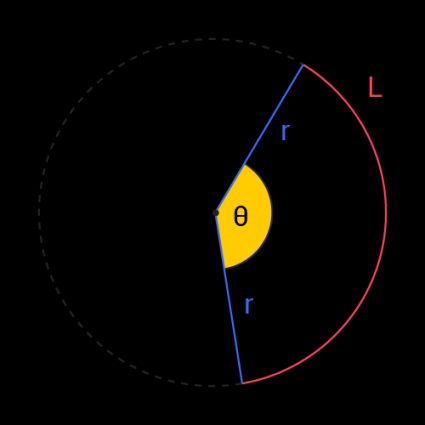
Kąt środkowy to kąt, którego wierzchołek znajduje się w środku koła, a jego ramiona rozciągają się do obwodu. Wyobraź sobie kąt środkowy jako kąt na czubku kawałka pizzy.

Możesz znaleźć kąt środkowy koła, używając wzoru:

θ = L / r

gdzie θ to kąt środkowy w radianach, L to długość łuku, a r to promień.

Prostota wzoru na kąt środkowy wynika z definicji radiana. Radian to jednostka miary kąta, gdzie 1 radian jest zdefiniowany jako kąt środkowy (θ), którego długość łuku jest równa promieniowi (L = r).

Ponieważ matematyka może sprawić, że ludzie robią się głodni, lepiej możemy zrozumieć kąt środkowy w kategoriach pizzy. Uwierz lub nie, pizze są świetnym przykładem do wyjaśniania parametrów koła, co możesz zobaczyć w naszym kalkulatorze rozmiaru pizzy 🇺🇸. Jaki byłby kąt środkowy kawałka pizzy, gdyby długość brzegu ($L$) była równa promieniowi ($r$)?

Ponieważ wiemy, że $L = r$, oraz że $1$ radian jest zdefiniowany jako kąt środkowy, gdy $L = r$, widzimy, że kąt środkowy to $1$ radian. Możemy również użyć wzoru na kąt środkowy w następujący sposób:

W przypadku pełnej okrągłej pizzy wiemy, że kąty środkowe wszystkich plasterków sumują się do 2π radianów = 360°. Ponieważ każdy kawałek ma kąt środkowy równy $1$ radianów, będziemy potrzebować $2\pi / 1 = 2\pi$ plasterków lub $6,28$ plasterków, aby wypełnić cały okrąg.

Otrzymamy tę samą odpowiedź, jeśli pomyślimy o tym problemie w kategoriach brzegu pizzy: oblicz obwód okręgu $2\pi r$. Ponieważ długość brzegu = promień, to $2\pi r / r = 2\pi$ brzegu zmieści się wzdłuż obwodu pizzy.

Teraz, jeśli nadal jesteś głodny/a, spójrz na kalkulator wycinka kołowego, aby obliczyć pole każdego kawałka pizzy!

Spróbuj użyć kalkulatora kąta środkowego odwrotnie, aby rozwiązać ten problem. Ziemia znajduje się w odległości około 149,6 mln km od Słońca. Jeśli Ziemia pokonuje około jednej czwartej swojej orbity w każdym sezonie, to ile kilometrów pokonuje Ziemia w każdym sezonie (np. od wiosny do lata)?

Rozwiążmy ten problem krok po kroku:

1. Uprośćmy problem zakładając, że orbita Ziemi jest kołowa (W rzeczywistości orbita Ziemi jest eliptyczna i ciągle się zmienia). W tym modelu Słońce znajduje się w środku okręgu, a orbita Ziemi jest jego obwodem.

2. Promień to odległość Ziemi od Słońca: $149,6$ mln km.

3. Kąt środkowy to ćwiartka okręgu: $360\degree / 4 = 90\degree$.

4. Użyjmy kalkulatora kąta środkowego, aby znaleźć długość łuku.

Możesz przeprowadzić obliczenia samodzielnie, zmieniając wzór na:

Następnie przekonwertuj kąt środkowy na radiany $90\degree = 1,57\ \mathrm{rad}$ (użyj naszego przelicznika kątów 🇺🇸, jeśli nie pamiętasz, jak to zrobić) i rozwiąż równanie:

Zakładając, że orbita jest idealnym kołem, Ziemia pokonuje około 234,9 mln km w każdym sezonie!