Calcolatore per il Valore p

Eccoci nel nostro calcolatore per il valore p! Non dovrai più chiederti come trovare il valore p o il p-value, perché qui potrai determinare i valore p unilaterali e bilaterali dei test statistici, seguendo tutte le distribuzioni più diffuse; normale, t di Student, chi-quadrato e F di Snedecor.

I valore p sono presenti in tutti i campi scientifici, ma molti trovano il concetto un po' intimidatorio. Non preoccuparti — in questo articolo ti spiegheremo non solo cos'è il valore p, ma anche come interpretare correttamente i valore p. Ti interessa sapere come calcolare il valore p a mano? Ti forniamo anche tutte le formule necessarie!

Formalmente, il valore p è la probabilità che la statistica del test produca valori almeno altrettanto estremi di quelli che ha prodotto per il tuo campione. È fondamentale ricordare che questa probabilità è è calcolata supponendo che l’ipotesi nulla H₀ sia vera!

Più intuitivamente, il valore p risponde alla domanda:

Supponendo di vivere in un mondo in cui l'ipotesi nulla è vera, qual è la probabilità che, per un altro campione, il test che sto eseguendo generi un valore almeno altrettanto estremo di quello che ho osservato per il campione che già possiedo?

È l'ipotesi alternativa che determina il significato di "estremo", quindi il valore p dipende dall'ipotesi alternativa dichiarata; unilaterale sinistra, unilaterale destra o bilaterale. Nelle formule seguenti, S sta per una statistica di prova, x per il valore che ha prodotto per un dato campione e Pr(evento | H₀) è la probabilità di un evento, calcolata sotto l'ipotesi che H₀ sia vera:

1. Test unilaterale sinistro: valore p = Pr(S ≤ x | H₀);

2. Test unilaterale destro: valore p = Pr(S ≥ x | H₀); e

3. Test bilaterale:

   valore p = 2 × min{Pr(S ≤ x | H₀), Pr(S ≥ x | H₀)}

   (Con min{a,b} indichiamo il numero minore tra a e b)

   Se la distribuzione della statistica del test sotto H₀ è simmetrica rispetto a 0, allora:
   valore p = 2 × Pr(S ≥ |x| | H₀)

   o, equivalentemente:
   valore p = 2 × Pr(S ≤ -|x| | H₀)

Poiché un'immagine vale più di mille parole, illustriamo queste definizioni. In questo caso, utilizziamo il fatto che la probabilità può essere ordinatamente rappresentata come l'area sotto la curva di densità per una data distribuzione. Forniamo due serie di immagini — una per una distribuzione simmetrica e l'altra per una distribuzione asimmetrica (non simmetrica).

• Caso simmetrico — distribuzione normale:

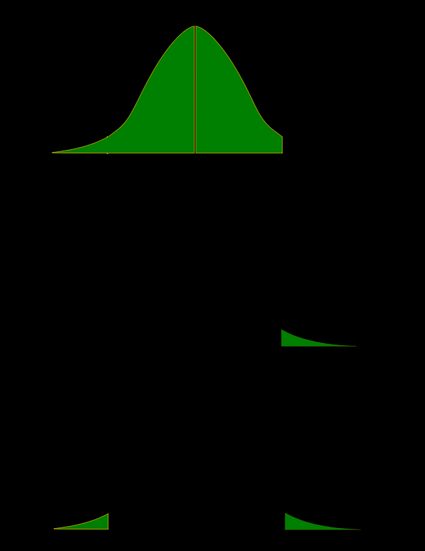
• Caso asimmetrico — distribuzione di chi-quadrato:

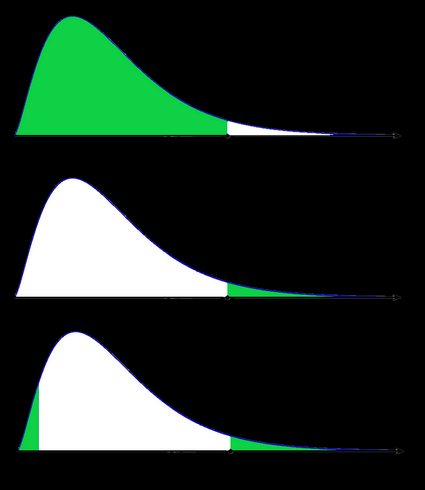
Nell'ultima immagine (il valore p bilaterale per una distribuzione asimmetrica), l'area del lato sinistro è uguale all'area del lato destro.

Per determinare il valore p, devi conoscere la distribuzione della tua statistica di test nell'ipotesi che l'ipotesi nulla sia vera. Quindi, con l'aiuto della funzione di distribuzione cumulativa (cdf) di questa distribuzione, possiamo esprimere la probabilità che la statistica del test sia almeno pari al suo valore x per il campione:

1. Test unilaterale sinistro:

   valore p = cdf(x);

2. Test unilaterale destro:

   valore p = 1 - cdf(x); e

3. Test bilaterale:

   valore p = 2 × min{cdf(x) , 1 - cdf(x)}.

   Se la distribuzione della statistica del test sotto H₀ è simmetrica rispetto a 0, allora il valore p della distribuzione bilaterale può essere semplificato in valore p = 2 × cdf(-|x|) o, equivalentemente, in valore p = 2 - 2 × cdf(|x|).

Le distribuzioni di probabilità più diffuse nei test di ipotesi tendono ad avere formule cdf complicate e trovare il valore p a mano potrebbe non essere possibile. Probabilmente dovrai ricorrere al computer o a una tabella statistica, dove sono stati raccolti i valori approssimativi della cdf.

Bene, ora sai come calcolare il valore p, ma...come mai devi calcolare questo numero? Nei test di ipotesi, l'approccio del valore p è un'alternativa all'approccio del valore critico. Ricordiamo che quest'ultimo richiede ai ricercatori di impostare in anticipo il livello di significatività, α, che è la probabilità di scartare l'ipotesi nulla quando è vera (quindi di errore di tipo I). Una volta ottenuto il valore p, basta confrontarlo con un dato α per decidere rapidamente se scartare o meno l'ipotesi nulla a quel livello di significatività α. Per maggiori dettagli, consulta la prossima sezione, dove spiegheremo come interpretare i valore p.

Come abbiamo detto sopra, il valore p è la risposta alla seguente domanda:

Supponendo di vivere in un mondo in cui l'ipotesi nulla è valida, qual è la probabilità che, per un altro campione, il test che sto eseguendo generi un valore almeno altrettanto estremo di quello osservato per il campione che ho già?

Cosa significa questo per te? Beh, hai due opzioni:

• Un valore p elevato significa che i tuoi dati sono altamente compatibili con l'ipotesi nulla; e
• Un valore p ridotto fornisce prove contro l'ipotesi nulla, in quanto significa che il tuo risultato sarebbe molto improbabile se l'ipotesi nulla fosse vera.

Tuttavia, può accadere che l'ipotesi nulla sia vera, ma che il tuo campione sia estremamente insolito! Ad esempio, immaginiamo di aver studiato l'effetto di un nuovo farmaco e di aver ottenuto un valore p di 0,03. Ciò significa che nel 3% degli studi simili, il caso sarebbe ancora in grado di produrre il valore della statistica del test che abbiamo ottenuto, o un valore ancora più estremo, anche nel caso in cui il farmaco non dovesse avere alcun effetto!

Alla domanda "cos'è il valore p" si può rispondere anche come segue — il valore p ha il minimo livello di significatività nel caso in cui l'ipotesi nulla è stata scartata. Quindi, se vuoi prendere una decisione sull'ipotesi nulla a un certo livello di significatività α, confronta il tuo valore p con α:

• Se il valore p è ≤ α, allora scarta l'ipotesi nulla e accetta l'ipotesi alternativa; o
• Se valore p ≥ α, allora non hai prove sufficienti per scartare l'ipotesi nulla.

Ovviamente, il destino dell'ipotesi nulla dipende da α. Ad esempio, se il valore p fosse 0,03, scarteremmo l'ipotesi nulla a un livello di significatività di 0,05, ma non a un livello di 0,01. Ecco perché il livello di significatività deve essere indicato in anticipo e non adattato opportunamente dopo che il valore p è stato stabilito! Un livello di significatività di 0,05 è il valore più comune, ma non ha nulla di magico. Qui puoi vedere a cosa può portare una fede troppo forte nella soglia di 0,05. È sempre meglio riportare il valore p e lasciare che il lettore tragga le proprie conclusioni.

Inoltre, tieni presente che la competenza nell'area tematica (e la buon senso) è fondamentale. Altrimenti, applicando senza criterio i principi statistici, puoi facilmente arrivare al valore statisticamente significativo, nonostante la conclusione sia falsa al 100%.

Con il nostro calcolatore per il valore p non dovrai più chiederti come trovare il valore p di tutti quei complicati test statistici! Ecco i passi da seguire:

1. Scegli l'ipotesi alternativa — bilaterale, unilaterale destr0 o unilaterale sinistro;

2. Indica la distribuzione della tua statistica di test sotto l'ipotesi nulla — è N(0,1), t si Student, chi-quadrato o F di Snedecor? Se non ti convince, consulta le sezioni seguenti, che sono dedicate a queste distribuzioni;

3. Se necessario, specifica i gradi di libertà della distribuzione della statistica del test;

4. Inserisci il valore della statistica del test calcolata per il tuo campione di dati; e

5. Il nostro calcolatore determina il valore p della statistica del test e fornisce la decisione da prendere sull'ipotesi nulla. Il livello di significatività standard è 0,05 per impostazione predefinita.

Passa alla modalità avanzata se vuoi aumentare la precisione con cui vengono eseguiti i calcoli o cambiare il livello di significatività.

In termini di funzione di distribuzione cumulativa (cdf) della distribuzione normale standard, tradizionalmente indicata con Φ, il valore p è dato dalle seguenti formule:

1. Z-test unilaterale sinistro:

   valore p = Φ(Z_punteggio);

2. Z-test unilaterale destro:

   valore p = 1 - Φ(Z_punteggio); o

3. Z-test bilaterale:

   valore p = 2 × Φ(-|Z_punteggio|)

   oppure

   valore p = 2 - 2 × Φ(|Z_punteggio|).

Utilizziamo il punteggio Z o Z-score se la statistica del test segue approssimativamente la distribuzione normale N(0,1). Grazie al teorema del limite centrale, puoi contare su questa approssimazione se disponi di un campione ampio (ad esempio almeno 50 punti dati) e se consideri la distribuzione normale.

Un test Z si riferisce più spesso alla verifica della media della popolazione o alla differenza tra due medie della popolazione, in particolare tra due proporzioni. I test Z si trovano anche nelle stime di massima verosimiglianza.

Il valore p del T-score o il punteggio T è dato dalle seguenti formule, in cui cdf_t,d indica la funzione di distribuzione cumulativa della distribuzione t di Student con d gradi di libertà:

1. Test t unilaterale sinistro:

   valore p = cdf_t,d(t_punteggio);

2. Test t unilaterale destro:

   valore p = 1 - cdf_t,d(t_punteggio); o

3. Test t bilaterale:

   valore p = 2 × cdf_t,d(-|t_punteggio|)

   oppure

   valore p = 2 - 2 × cdf_t,d(|t_punteggio|).

Usa l'opzione punteggio T se la statistica del test segue la distribuzione t di Student. Questa distribuzione ha una forma simile a quella di N(0,1) (a campana e simmetrica) ma ha code più pesanti — la forma esatta dipende dal parametro chiamato gradi di libertà. Se il numero di gradi di libertà è elevato (>30), cosa che generalmente accade per i campioni di grandi dimensioni, la distribuzione t di Student è praticamente indistinguibile dalla distribuzione normale N(0,1).

I test t più comuni sono quelli per le medie di una popolazione con una deviazione standard sconosciuta, oppure per la differenza tra le medie di due popolazioni, con deviazioni standard uguali o disuguali, ma sconosciute. Esiste anche un test t per campioni accoppiati (dipendenti).

Usa l'opzione χ²-score quando esegui un test in cui la statistica del test segue la distribuzione di χ².

Questa distribuzione si verifica se, ad esempio, prendi la somma di variabili al quadrato, ognuna delle quali segue la distribuzione normale N(0,1). Ricordati di controllare il numero di gradi di libertà della distribuzione χ² della tua statistica di prova!

Come trovare il valore p dal punteggio chi-quadrato? Puoi farlo con l'aiuto delle seguenti formule, in cui cdf_χ²,d indica la funzione di distribuzione cumulativa della distribuzione χ² con d gradi di libertà:

1. Test del χ² unilaterale sinistro:

   valore p = cdf_χ²,d(χ²_punteggio);

2. Test del χ² unilaterale destro:

   valore p = 1 - cdf_χ²,d(χ²_punteggio)

   Ricorda che i test χ² per la bontà dell'adattamento e l'indipendenza sono test unilaterale destro! (vedi sotto); o

3. Test χ² a bilaterale:

   valore p = 2 × min{cdf_χ²,d(χ²_punteggio), 1 - cdf_χ²,d(χ²_punteggio)}

   (Con min{a,b} indichiamo il più piccolo dei numeri a e b).

I test più diffusi che portano a un punteggio di χ² sono i seguenti:

• Verifica se la varianza dei dati normalmente distribuiti ha un valore predeterminato. In questo caso, la statistica del test ha una distribuzione χ² con n - 1 gradi di libertà, dove n è la dimensione del campione. Può trattarsi di un test unilaterale o bilaterale.

• Il test di idoneità verifica se la distribuzione empirica (del campione) concorda con una distribuzione di probabilità prevista. In questo caso, la statistica del test segue la distribuzione χ² con k - 1 gradi di libertà, dove k è il numero di classi in cui è suddiviso il campione. Si tratta di un test unilaterale destro.

• Il test di indipendenza viene utilizzato per determinare se esiste una relazione statisticamente significativa tra due variabili. In questo caso, la statistica del test si basa sulla tabella di contingenza e segue la distribuzione χ² con (r - 1)(c - 1) gradi di libertà, dove r è il numero di righe e c è il numero di colonne della tabella di contingenza. Anche questo è un test unilaterale destro.

Infine, l'opzione misura F deve essere utilizzata quando si esegue un test in cui la statistica del test segue la distribuzione F, nota anche come distribuzione di Fisher-Snedecor. La forma esatta di una distribuzione F dipende da due gradi di libertà.

Per capire da dove provengono questi gradi di libertà, considera le variabili casuali indipendenti X e Y, che seguono entrambe la distribuzione χ² con d₁ e d₂ gradi di libertà, rispettivamente. In questo caso, il rapporto (X/d₁)/(Y/d₂) segue la distribuzione F, con (d₁, d₂) gradi di libertà. Per questo motivo, i due parametri d₁ e d₂ sono chiamati anche gradi di libertà del numeratore e del denominatore.

Il valore p della misura F o il punteggio F è dato dalle seguenti formule, dove lasciamo che cdf_F,d1,d2 indichi la funzione di distribuzione cumulativa della distribuzione F, con (d₁, d₂) gradi di libertà:

1. Test F unilaterale sinistro:

   valore p = cdf_F,d1,d2(F_punteggio);

2. Test F unilaterale destro:

   valore p = 1 - cdf_F,d1,d2(F_punteggio); o

3. Test F bilaterale:

   valore p = 2 × min{cdf_F,d1,d2(F_punteggio), 1 - cdf_F,d1,d2(F_punteggio)}

   (Con min{a,b} indichiamo il più piccolo dei numeri a e b).

Di seguito elenchiamo i test più importanti che producono gli misura F. Tutti i test sono unilaterali destri.

• Un test per la disparità delle varianze in due popolazioni normalmente distribuite. La sua statistica segue la distribuzione F con (n - 1, m - 1) gradi di libertà, dove n e m sono le rispettive dimensioni del campione.

• L'analisi della varianza, ANOVA, viene utilizzata per testare l'uguaglianza delle medie in tre o più gruppi che provengono da popolazioni normalmente distribuite con varianze uguali. Si ottiene la distribuzione F con (k - 1, n - k) gradi di libertà, dove k è il numero di gruppi e n è la dimensione totale del campione (in tutti i gruppi).

• Un test per la significatività complessiva dell'analisi di regressione. La statistica del test ha una distribuzione F con (k - 1, n - k) gradi di libertà, dove n è la dimensione del campione e k è il numero di variabili (inclusa l'intercetta).

  Una volta stabilita la presenza della relazione lineare nel tuo campione di dati con il test di cui sopra, puoi calcolare il coefficiente di determinazione, R², che indica la forza di questa relazione. Puoi farlo a mano o utilizzare il nostro calcolatore del coefficiente di determinazione 🇺🇸.

• Un test per confrontare due modelli di regressione annidati. La statistica del test segue la distribuzione F con (k₂ - k₁, n - k₂) gradi di libertà, dove k₁ e k₂ sono rispettivamente il numero di variabili nel modello più piccolo e in quello più grande e n è la dimensione del campione.

  Potrai notare che il test F di significatività globale è una forma particolare del test F per il confronto di due modelli annidati: verifica se il nostro modello è significativamente migliore del modello senza predittori (cioè il modello lineare).

No, il valore p non può essere negativo. Perché le probabilità non possono essere negative e il valore p è la probabilità che la statistica del test soddisfi determinate condizioni.

Un valore p elevato significa che, in base all'ipotesi nulla, c'è un'alta probabilità che per un altro campione la statistica di prova generi un valore almeno altrettanto estremo di quello osservato nel campione già in tuo possesso. Un valore p elevato non consente di scartare l'ipotesi nulla.

Un valore p basso significa che, in base all'ipotesi nulla, c'è poca probabilità che per un altro campione la statistica di prova generi un valore almeno altrettanto estremo di quello osservato per il campione di cui si dispone. Un valore p basso è una prova a favore dell'ipotesi alternativa — ti permette di scartare l'ipotesi nulla.