Calcolatore della Distribuzione Normale

Questo calcolatore della distribuzione normale (anche calcolatore della curva a campana) calcola l'area sotto una curva a campana e stabilisce la probabilità che un valore sia superiore o inferiore a qualsiasi valore arbitrario X. Puoi anche usare questo calcolatore della distribuzione di probabilità per trovare la probabilità che la tua variabile si trovi in un intervallo arbitrario, da X a X₂, semplicemente usando i valori della distribuzione normale della media e della deviazione standard. Questo articolo spiega alcuni termini di base relativi alla distribuzione normale standardizzata, fornisce la formula della funzione di ripartizione, (anche detta CDF o funzione di ripartizione), e fornisce esempi di distribuzione normale di probabilità.

La distribuzione normale (nota anche come distribuzione gaussiana) è una distribuzione di probabilità continua. La maggior parte dei dati si avvicina a un valore centrale, senza alcuna distorsione verso destra o verso sinistra. Molte osservazioni in natura, come l'altezza delle persone o la pressione sanguigna, seguono questa distribuzione.

In una distribuzione normale, il valore medio è anche la mediana (il numero "centrale" di un elenco ordinato di dati) e la moda (il valore con la maggiore frequenza di occorrenza). Poiché questa distribuzione è simmetrica rispetto al centro, il 50% dei valori è inferiore alla media e il 50% dei valori è superiore alla media.

Un altro parametro che caratterizza la distribuzione normale standardizzata è la deviazione standard 🇺🇸. Descrive l'ampiezza dei numeri. In generale, il 68% dei valori dovrebbe rientrare in una deviazione standard dalla media, il 95% in 2 deviazioni standard e il 99,7% in 3 deviazioni standard. Il numero di deviazioni standard dalla media è chiamato punteggio Z. Può capitare di conoscere la varianza ma non la deviazione standard della distribuzione. Tuttavia, è facile calcolare quest'ultima semplicemente prendendo la radice quadrata della varianza.

Si può dire che un aumento del valore medio sposta l'intera curva a campana verso destra. Le variazioni della deviazione standard restringono o allargano la distribuzione intorno alla media. Nelle distribuzioni fortemente disperse, c'è una maggiore probabilità che un punto di dati casuale si allontani dalla media. La forma della curva a campana è determinata solo da questi due parametri.

È possibile standardizzare qualsiasi distribuzione normale attraverso un processo noto come punteggio standard. Si tratta di sottrarre la media della popolazione dal punteggio dei dati e dividere la differenza per la deviazione standard della popolazione. Una distribuzione normale standardizzata ha le seguenti proprietà:

• Il valore medio è uguale a 0;
• La deviazione standard è uguale a 1;
• L'area totale sotto la curva è uguale a 1; e
• Ogni valore della variabile x viene convertito nel corrispondente punteggio Z.

Puoi verificare questo strumento anche utilizzando il calcolatore della distribuzione normale standardizzata. Se inserisci la media, μ, come 0 e la deviazione standard, σ, come 1, il punteggio Z sarà uguale a X.

L'area totale sotto la curva della distribuzione normale standardizzata è uguale a 1. Ciò significa che corrisponde alla probabilità. Puoi calcolare la probabilità che il tuo valore sia inferiore a qualsiasi valore arbitrario X (indicato come P(x < X)) come area sotto il grafico a sinistra del punteggio Z di X.

Diamo un'altra occhiata al grafico precedente e consideriamo i valori della distribuzione entro una deviazione standard. Si può notare che la probabilità rimanente (0,32) è composta da due regioni. La coda di destra e la coda di sinistra della distribuzione normale sono simmetriche, ciascuna con un'area di 0,16. Questa bellezza matematica è il motivo per cui i data scientist amano la distribuzione gaussiana!

Calcolare l'area sotto il grafico non è un compito facile. Puoi utilizzare la tabella di distribuzione normale o provare a integrare la funzione cumulativa normale:

Ad esempio, supponiamo che tu voglia trovare la probabilità che una variabile sia inferiore a $x$. In questo caso, devi integrare questa funzione da meno infinito a $x$. Allo stesso modo, se vuoi trovare la probabilità che la variabile sia superiore a $x$, devi integrare questa funzione da $x$ a infinito. Per maggiori informazioni su questo argomento, consulta il calcolatore per il valore p.

Puoi anche usare questo calcolatore come un calcolatore della funzione di ripartizione!

Nota, tuttavia, che la funzione di ripartizione non deve essere confusa con la sua funzione di densità (la curva a campana), che assegna semplicemente il valore di probabilità a tutti gli argomenti:

Per definizione, la funzione di densità è la derivata prima, cioè il tasso di variazione della funzione di ripartizione.

1. Decidi la media della tua distribuzione normale. Ad esempio, possiamo provare ad analizzare la distribuzione dell'altezza di donne italiane di 20 anni. L'altezza media di una donna 20enne è 168 cm;

2. Scegli la deviazione standard della tua serie di dati. Diciamo che è pari a 12 cm;

3. Supponiamo che tu voglia utilizzare questo calcolatore per la curva a campana per determinare la probabilità di una donna di essere più alta di 180 cm. Allora, il tuo $X$ sarà uguale a 180 cm;

4. Il nostro calcolatore della distribuzione normale mostrerà due valori: la probabilità che una persona sia più alta di 180 cm ($P(x > X)$) e più bassa di 180 cm ($P(x < X)$). In questo caso, la prima è pari al 15,86% e la seconda all'84,13%; e

5. Puoi anche aprire la Modalità avanzata del calcolatore per calcolare la probabilità che una variabile $x$ sia compresa in un determinato intervallo (da X a X₂). Ad esempio, la probabilità che l'altezza di una donna italiana 20enne sia compresa tra 180 e 190 cm è pari al 12,52%.

La distribuzione normale descrive molti fenomeni naturali: processi che avvengono continuamente e su larga scala. Secondo la legge dei grandi numeri, il valore medio di un campione di dimensioni sufficientemente grandi, se estratto da una distribuzione, sarà vicino alla media della distribuzione sottostante. Più misure si effettuano, più ci si avvicina al valore effettivo della media della popolazione.

Tuttavia, tieni presente che una delle tendenze statistiche più solide è la regressione verso la media. Coniato da un famoso scienziato britannico Francis Galton, questo termine ci ricorda che le cose tendono ad uniformarsi nel tempo. I genitori più alti tendono ad avere, in media, figli con un'altezza più vicina alla media. Dopo un periodo di crescita elevata del PIL (prodotto interno lordo), un paese tende a vivere un paio di anni di produzione totale più moderata.

Spesso può accadere che la variazione naturale, nei dati ripetuti, assomigli molto a un cambiamento reale. Tuttavia, è solo un fatto statistico che osservazioni relativamente alte (o basse) sono spesso seguite da altre con valori più vicini alla media. La regressione verso la media è spesso fonte di prove aneddotiche che non possiamo confermare su basi statistiche.

La distribuzione normale è nota per le sue probabilità matematiche. Varie probabilità, sia discrete che continue, tendono a convergere verso la distribuzione normale. Questo si chiama teorema del limite centrale ed è chiaramente uno dei teoremi più importanti della statistica. Grazie a questo teorema, puoi usare il calcolatore della distribuzione normale della media e della deviazione standard per simulare la distribuzione anche dei più grandi insiemi di dati.

Quando la dimensione del campione diventa sempre più grande, il valore medio si avvicina alla normalità, indipendentemente dalla forma iniziale della distribuzione della popolazione. Ad esempio, con un numero sufficientemente grande di osservazioni, la distribuzione normale può essere utilizzata per approssimare la distribuzione di Poisson o la distribuzione di probabilità binomiale. Di conseguenza, spesso consideriamo la distribuzione normale come la distribuzione limite di una sequenza di variabili aleatorie.

Ecco perché le migliori pratiche dicono che molti test e procedure statistiche necessitano di un campione di più di 30 punti dati per garantire il raggiungimento di una distribuzione normale. Nel linguaggio statistico, tali proprietà sono spesso chiamate asintotiche.

Se non sai di quale sia la distribuzione di base dei tuoi dati, ma puoi ottenere un gran numero di osservazioni, puoi fidarti del fatto che seguano la distribuzione normale. Questo vale anche per i fenomeni di passeggiata aleatoria, ovvero processi che si evolvono senza un modello o una tendenza riconoscibile.

Una tabella di distribuzione normale standardizzata, come quella qui sotto, è un ottimo punto di partenza per controllare i valori di riferimento quando si costruiscono gli intervalli di confidenza. Puoi utilizzare il nostro calcolatore della distribuzione normale di probabilità per verificare che il valore utilizzato per costruire gli intervalli di confidenza sia corretto. Ad esempio, se X = 1,96, allora X è il 97,5° percentile della distribuzione normale standardizzata. (Imposta la media = 0, la deviazione standard = 1 e X = 1,96). Osserva che il 97,5% dei valori è inferiore alla X)

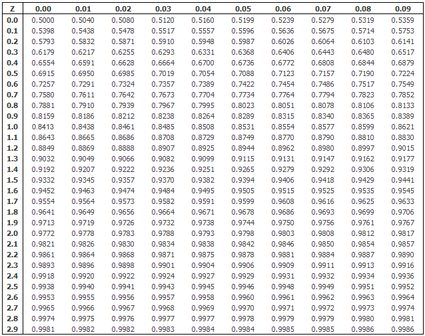
Inoltre, se l'osservazione utilizzata è casuale e indipendente, anche i valori della media e della varianza della popolazione stimati dal campione sono indipendenti. La distribuzione gaussiana univariata (calcolata per una singola variabile) può anche essere generalizzata per un insieme di variabili. Una "somma" specifica chiamata distribuzione normale multivariata mostra la distribuzione congiunta di un particolare numero di variabili. Si può utilizzare per modellare dati di dimensioni più elevate, come ad esempio una valutazione completa dei pazienti.

Gli statistici basano molti tipi di test statistici sul presupposto che le osservazioni utilizzate nella procedura di test seguano la distribuzione gaussiana. È valida per quasi tutte le statistiche inferenziali quando si utilizzano le informazioni del campione per fare generalizzazioni sull'intera popolazione.

Ad esempio, puoi verificare formalmente se il valore stimato di un parametro è statisticamente diverso da zero o se il valore medio di una popolazione è uguale all'altra. La maggior parte dei semplici test che ti aiutano a rispondere a queste domande (i cosiddetti test parametrici) si basano sulla presunzione di normalità. Non è possibile utilizzarla quando una distribuzione empirica ha proprietà diverse da quella normale.

Dovresti verificare questa ipotesi prima di applicare questi test. Esistono un paio di test di normalità molto diffusi per determinare se la distribuzione dei dati è normale. Il test di Shapiro-Wilk basa la sua analisi sulla varianza del campione. Il test di Jarque-Bera, invece, si basa sull'asimmetria e sull'eccesso di curtosi della distribuzione empirica. Entrambi i test consentono un'interpretazione precisa e mantengono il potere esplicativo dei modelli statistici.

Il test di normalità ti aiuta anche a verificare se puoi aspettarti tassi di rendimento in eccesso su attività finanziarie, come le azioni, o quanto il tuo portfolio sia performante rispetto al mercato. Possiamo utilizzare la media della distribuzione empirica per approssimare l'efficacia del tuo investimento. D'altro canto, è possibile utilizzare la varianza per valutare il rischio che caratterizza un portfolio.

Una delle ipotesi di normalità più comunemente utilizzate riguarda i modelli di regressione lineare (o anche non lineare). In genere, si suppone che i residui dello stimatore dei minimi quadrati seguano una distribuzione normale standardizzata con un valore medio pari a zero e una deviazione standard fissa (variabile nel tempo). Puoi pensare a questi residui come a una distanza dalla retta di regressione dai punti dati effettivi. Puoi valutare l'efficacia dell'adattamento del modello dei minimi quadrati utilizzando il test chi quadrato. Tuttavia, se la distribuzione degli errori non è normale, potrebbe significare che le stime sono distorte o inefficaci.

Un altro esempio importante in quest'area è l'ANOVA (analisi della varianza), utilizzata per verificare se i valori medi di due campioni sono uguali. L'ANOVA può essere eseguita con successo anche nella forma canonica quando la distribuzione dei residui del modello è normale.

Ci sono diversi modi in cui la distribuzione dei dati può discostarsi dalla distribuzione a campana, ma i due più importanti sono:

• Code grasse — I valori estremi possono verificarsi con una probabilità maggiore (ad esempio, c'è una probabilità relativamente alta di ottenere risultati anomali);
• Asimmetria — La distribuzione è asimmetrica. I valori medi e mediani della distribuzione sono diversi (ad esempio, la dispersione dei salari nel mercato del lavoro).

Le distribuzioni non normali sono comuni in finanza, ma puoi aspettarti che lo stesso tipo di problemi compaia anche in psicologia o negli studi sociali. Uno dei tanti esempi di queste distribuzioni è la distribuzione geometrica, adatta a modellare una serie di eventi indipendenti, ad esempio il risultato del lancio di un dado.

La distribuzione normale (o distribuzione gaussiana) è una distribuzione di probabilità a forma di "campana" per variabili aleatorie indipendenti. È fondamentale per la statistica perché descrive in modo preciso la distribuzione dei valori di molti fenomeni naturali. La curva di distribuzione è simmetrica intorno alla sua media, con la maggior parte delle osservazioni raggruppate intorno a un picco centrale e con una diminuzione delle probabilità per i valori più lontani dalla media in entrambe le direzioni.

Sì, una distribuzione normale può avere una grande deviazione standard rispetto alla media. Ad esempio, una distribuzione normale standardizzata può avere una media di 6, ma una deviazione standard di 20. In generale, più larga è la distribuzione normale rispetto alla media, più grande è la sua deviazione standard.

Per determinare se un insieme di dati è distribuito normalmente:

1. Disegna un grafico della distribuzione dei dati;
2. Verifica che la curva abbia la forma di una campana simmetrica centrata intorno alla media; e
3. Verifica la regola empirica: il 68% dei valori deve rientrare in una deviazione standard dalla media, il 95% in 2 deviazioni standard e il 99,7% in 3 deviazioni standard.

I due parametri principali della distribuzione normale sono: la media (μ) e la deviazione standard (σ). μ determina la posizione del picco della distribuzione normale sull'asse numerico. σ è un parametro di scala che fa sì che la distribuzione normale si distribuisca maggiormente con valori più grandi di σ.

2,5%, supponendo che per una quercia la distribuzione normale della circonferenza abbia μ = 150 cm e σ = 30 cm.

1. Segna la distribuzione normale con il picco a μ = 150 cm e σ = 30 cm;
2. Nota che la circonferenza di 210 cm è 2σ = 60 cm sopra la media;
3. Utilizza la regola empirica secondo cui il 95% dei dati è compreso tra ±2σ; e
4. Dividi per 2 per prendere gli alberi con una circonferenza superiore a +2σ.