Calcolatore di Probabilità

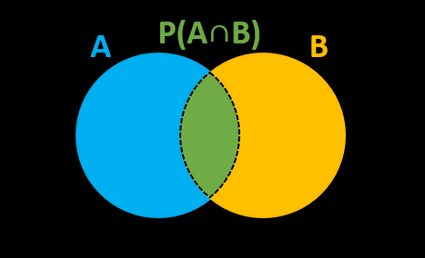
Con il calcolatore di probabilità, puoi investigare le relazioni di probabilità tra due eventi distinti. Ad esempio, se la probabilità che un evento A se ne verifichi è del 50% e lo stesso vale per B, quali sono le probabilità che se ne verifichino entrambi, che se ne verifichi solo uno, che se ne verifichi almeno uno o che non se ne verifichi nessuno e così via.

Il nostro calcolatore di probabilità ti offre sei scenari, più altri 6 se inserisci quante volte il "dado è tratto", per così dire. Se sai come calcolare la probabilità dei singoli eventi con esempi e esercizi pratici, ti farà risparmiare molto tempo.

Continuando a leggere qui di seguito, potrai:

• Scoprire come utilizzare correttamente il calcolatore di probabilità;
• Scoprire come si calcola la probabilità di singoli eventi;
• Leggere diversi esempi di utilizzo della probabilità, comprese le formule di probabilità condizionata;
• Studiare la differenza tra probabilità teorica ed empirica; e
• Aumentare le tue conoscenze sulla relazione tra probabilità e statistica.

Sei qui apposta per verificare le tue probabilità di vincere una scommessa o di vincere il jackpot? Risolvi i problemi di probabilità online con i nostri calcolatore per la probabilità di successo e calcolatore per la lotteria 🇺🇸!

La definizione di base di probabilità è il rapporto tra tutti i risultati favorevoli e il numero di tutti i risultati possibili.

I valori ammessi di una singola probabilità variano da 0 a 1, quindi è conveniente scrivere le probabilità anche come percentuali. La probabilità di un singolo evento può essere espressa come segue:

• La probabilità di A: P(A);
• La probabilità di B: P(B);
• La probabilità di +: P(+);
• La probabilità di ♥: P(♥) ecc.

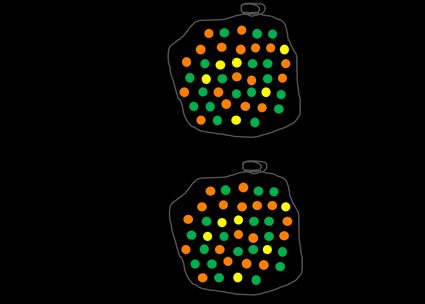
Vediamo un esempio con biglie multicolore. Abbiamo un sacchetto pieno di biglie arancioni, verdi e gialle. Il nostro evento A è prendere una biglia a caso dal sacchetto. Possiamo definire Ω come un insieme completo di biglie. La probabilità dell'evento Ω, che significa scegliere una biglia qualsiasi, è naturalmente 1. Infatti, la somma di tutti gli eventi possibili in un dato insieme è sempre uguale a 1.

Ora vediamo qualcosa di più impegnativo — qual è la probabilità di scegliere una biglia arancione? Per rispondere a questa domanda, devi trovare il numero di tutte le biglie arancioni e dividerlo per il numero di tutte le biglie presenti nel sacchetto. Puoi farlo per qualsiasi colore, ad esempio il giallo, e noterai senza dubbio che più sono le biglie di un determinato colore, più alta è la probabilità di sceglierlo dal sacchetto se il processo è totalmente casuale.

Dai un'occhiata al nostro calcolatore di probabilità con 3 eventi 🇺🇸 e il calcolatore di probabilità condizionata 🇺🇸 per determinare le probabilità di eventi multipli online.

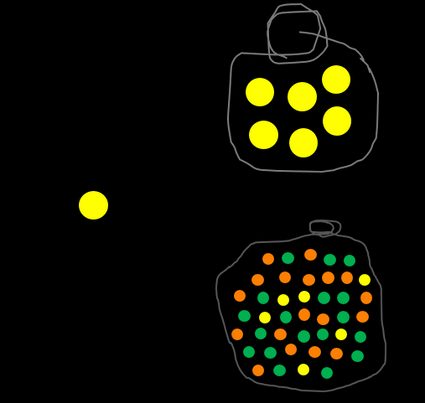
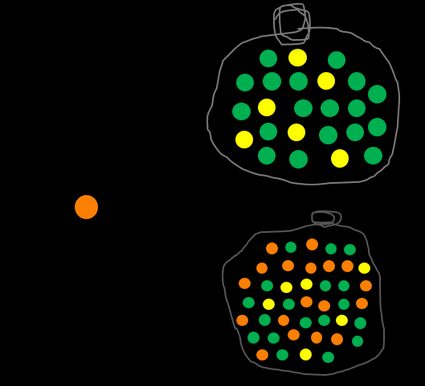
Possiamo definire un evento complementare, scritto come Ā o A', che significa non A. Nel nostro esempio, la probabilità di NON scegliere una biglia arancione è valutata come il numero di tutte quelle non arancioni diviso per tutte le biglie. Il calcolo della probabilità P(A) + P(Ā) è sempre 1 perché non ci sono altre opzioni come la metà di una biglia o una biglia semi-arancione.

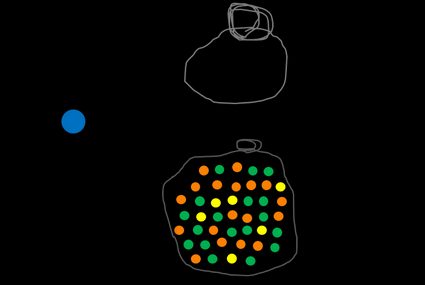
Ora cerca di fare il calcolo della probabilità di ottenere una biglia blu. Non importa quanto ci provi, fallirai perché non ce n'è nemmeno una nel sacchetto, quindi il risultato è uguale a 0.

Utilizziamo sempre calcoli intuitivi di probabilità. Sapere come quantificare la probabilità è essenziale per l'analisi statistica. Ti permette di misurare questo concetto altrimenti oscuro chiamato "probabilità". Inoltre, dato un insieme di dati discreti, la frequenza relativa per ogni valore è sinonimo di probabilità di accadimento.

Stai cercando qualcosa di un po' diverso? Dai un'occhiata al nostro calcolatore di probabilità post-test 🇺🇸. 🎲

Per sfruttare al meglio il nostro calcolatore, dovrai seguire i seguenti passi:

1. Definisci il problema di probabilità che vuoi risolvere.
Il tuo problema deve essere condensato in due eventi indipendenti.

2. Trova la probabilità di ogni evento.
Ora che sai come stimare la probabilità di un singolo evento, devi solo eseguire il compito e ottenere tutti i valori necessari.

3. Inserisci la percentuale di probabilità di ogni evento nei campi corrispondenti.
Una volta inseriti, il calcolatore di probabilità si popolerà immediatamente con l'esatta probabilità di 6 diversi scenari:

• Entrambi gli eventi si verificheranno;
• Almeno uno degli eventi si verificherà;
• Si verificherà esattamente uno degli eventi;
• Nessuno dei due eventi si verificherà;
• Solo il primo evento non si verificherà; e
• Solo il secondo evento non si verificherà.

Puoi anche scegliere di visualizzare tutti i casi precedenti. Inoltre, il calcolatore può anche mostrare la probabilità di altri 6 scenari, dato un certo numero di prove:

• A si verifica sempre;
• A non si verifica mai;
• A si verifica almeno una volta;
• B si verifica sempre;
• B non si verifica mai; e
• B si verifica almeno una volta.

Puoi modificare il numero di prove e qualsiasi altro campo del calcolatore, siccome gli altri campi si adatteranno automaticamente. Questa funzione ti fa risparmiare un sacco di tempo se vuoi scoprire, ad esempio, quale dovrebbe essere la probabilità dell'evento B per far sì che la probabilità che entrambi si verifichino sia del 50%.

Se l'insieme delle scelte possibili è estremamente ampio e solo pochi risultati vanno a buon fine, la probabilità risultante è minima, come P(A) = 0,0001. È conveniente utilizzare la notazione scientifica per non confondere il numero di zeri.

Una delle considerazioni più importanti nel mondo delle probabilità è la dipendenza o l'indipendenza degli eventi. Due eventi sono indipendenti se il verificarsi del primo non influisce sulla probabilità che si verifichi il secondo. Ad esempio, se lanciamo un dado cubico standard perfettamente bilanciato, la probabilità di ottenere un due ⚁ è pari a 1/6 (la stessa di ottenere un quattro ⚃ o qualsiasi altro numero).

Supponiamo di avere due lanci di dadi e di ottenere un cinque ⚄ nel primo. Se ti chiedi qual è la probabilità di ottenere un due ⚁ nel secondo lancio del dado, la risposta è 1/6 ancora una volta a causa dell'indipendenza degli eventi.

Il modo di pensare, così come i calcoli, cambiano se uno degli eventi interrompe l'intero sistema. Questa volta parliamo di probabilità condizionata.

Supponiamo di avere 10 diverse palle da biliardo numerate, da ➀ a ➉. Scegli una palla a caso, quindi la probabilità di ottenere la ➆ è esattamente 1/10. Supponiamo che tu abbia scelto i tre ➂ e che li abbia rimossi dal gioco. Poi ti chiedi, ancora una volta, qual è la probabilità di ottenere il sette ➆. La situazione è cambiata perché c'è una sola pallina con ➆ su nove possibilità, il che significa che la probabilità è ora 1/9. In altre parole, la domanda può essere posta: "Qual è la probabilità di scegliere ➆, SE la prima pallina era ➂?"

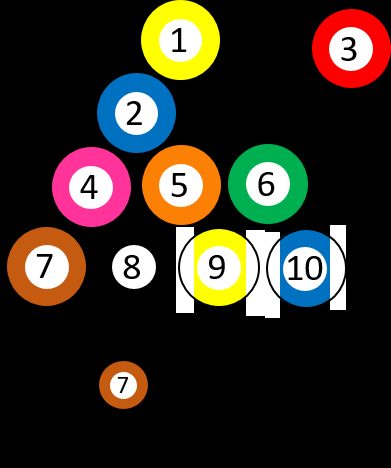
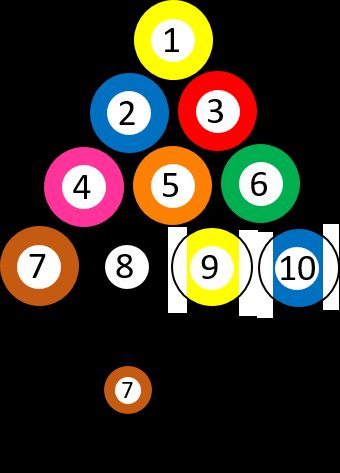
Facciamo un altro esempio — immagina di dover sostenere un esame di statistica. Sai dai tuoi colleghi più anziani che si tratta di un esame impegnativo e che la probabilità che tu lo superi al primo trimestre è di 0,5 (l'anno scorso sono passati 18 su 36 studenti). Allora poniti una domanda: "Qual è la probabilità di passare se hai già studiato l'argomento?" — 20 persone hanno ammesso di aver rivisto i loro appunti almeno una volta prima dell'esame e 16 di queste hanno avuto successo, il che significa che la risposta all'ultima domanda è 0,8. Questo risultato indica che questa condizione aggiuntiva è davvero importante se vogliamo scoprire se studiare cambia qualcosa o meno.

Se il concetto di probabilità condizionata ancora non ti è chiaro alla domanda "Come si calcola la probabilità?", proviamo con un altro esempio — devi andare in auto dalla città X alla città Y. La distanza tra le due città è di circa 150 chilometri. La distanza che li separa è di circa 150 chilometri. Con il serbatoio pieno, di solito puoi percorrere fino a 400 chilometri. Se non conosci il livello di carburante, puoi stimare la probabilità di raggiungere la destinazione senza fare rifornimento. E se qualcuno ha già fatto il pieno? Ora sei quasi sicuro di farcela, a meno che altri problemi non lo impediscano.

L'espressione formale della probabilità condizionata, che può essere indicata come P(A|B), P(A/B) o P_B(A), può essere calcolata per:

P(A|B) = P(A∩B) / P(B),

dove P(B) è la probabilità di un evento B e P(A∩B) è la probabilità congiunta di entrambi gli eventi. D'altra parte, possiamo stimare l'intersezione di due eventi se conosciamo una delle probabilità condizionali con il calcolo:

• P(A∩B) = P(A|B) × P(B); oppure
• P(A∩B) = P(B|A) × P(A).

È meglio comprendere il concetto di formula della probabilità condizionata con i diagrammi ad albero. Chiediamo agli studenti di una classe se amano la matematica e la fisica. L'evento M indica la percentuale di studenti a cui piace la matematica e P lo stesso per la fisica:

Esiste un famoso teorema che mette in relazione le probabilità condizionate di due eventi. Si chiama teorema di Bayes e la formula è la seguente:

P(A|B) = P(B|A) × P(A) / P(B)

Puoi fare una domanda — "Qual è la probabilità di A data B se conosco la probabilità di B data A?". Questo teorema a volte fornisce risultati sorprendenti e poco intuitivi. Gli esempi più comuni sono i test antidroga e l'individuazione delle malattie, che hanno molto in comune con il rischio relativo di malattia nella popolazione. Soffermiamoci sul secondo. In un gruppo di 1000 persone, 10 di loro hanno una malattia rara. Tutti hanno fatto un test, che mostra il risultato effettivo nel 95% dei casi. Ora vogliamo trovare la probabilità che una persona si ammali se il risultato del test è positivo.

Senza pensarci, potresti prevedere, per intuizione, che il risultato dovrebbe essere intorno al 90%, giusto? Facciamo qualche calcolo di probabilità per stimare la risposta corretta.

1. Utilizzeremo una notazione: S — sano, M — malato, + — test positivo, - — test negativo;

2. Riscrivi le informazioni del testo precedente in termini di probabilità: P(S) = 0,99, P(M) = 0,01, P(+|M) = 0,95, P(-|M) = 0,05, P(+|S) = 0,05, P(-|S) = 0,95;

3. Calcola la probabilità totale di un test positivo: P(+) = P(+|M) × P(M) + P(+|S) × P(S) = 0,95 × 0,01 + 0,05 × 0,99 = 0,059; e

4. Usa il teorema di Bayes per trovare la probabilità condizionata P(M|+) = P(+|M) × P(M) / P(+) = 0,95 × 0,01 / 0,059 = 0,161.

Hmm... non è così alto, vero? Si scopre che questo tipo di paradosso si verifica se c'è un significativo squilibrio tra il numero di persone sane e malate o, in generale, tra due gruppi distinti. Se il risultato è positivo, vale sempre la pena ripetere il test per fare una diagnosi appropriata.

Possiamo distinguere due tipi di distribuzioni di probabilità, a seconda che le variabili casuali siano discrete o continue.

• Una distribuzione di probabilità discreta descrive la probabilità che si verifichino eventi contati e distinti. Uno degli esempi è la probabilità binomiale, che tiene conto della probabilità di successo in più turni, ad esempio nel lancio di una moneta. Al contrario, nella distribuzione di Pascal (nota anche come binomiale negativa) viene dato un numero fisso di successi e si vuole stimare il numero totale di prove.

  La distribuzione di Poisson è un'altra distribuzione di probabilità discreta ed è in realtà un caso particolare di quella binomiale, che puoi calcolare con il nostro calcolatore per la distribuzione di Poisson 🇺🇸. La funzione di massa di probabilità può essere interpretata come un'altra definizione di distribuzione di probabilità discreta — assegna un determinato valore a qualsiasi numero separato. La distribuzione geometrica 🇺🇸 è un ottimo esempio di utilizzo della funzione di massa di probabilità.

• Una distribuzione di probabilità continua contiene informazioni su eventi non numerabili. Non è possibile prevedere la probabilità di un singolo evento (come in una distribuzione discreta), ma piuttosto di trovare l'evento in un certo intervallo di variabili. La distribuzione normale è una delle distribuzioni continue più conosciute. Descrive una serie di proprietà all'interno di qualsiasi popolazione, ad esempio l'altezza delle persone adulte o la distribuzione del QI. La funzione che descrive la probabilità di vedere un risultato in un determinato intervallo di valori è chiamata funzione di densità di probabilità.

Se già conosci bene la teoria delle probabilità e di calcoli, dovrai sicuramente confrontarti con la distribuzione SMp(x) 🇺🇸, che tiene conto della combinazione di diverse funzioni di probabilità discrete e continue.

Per ogni distribuzione di probabilità, possiamo costruire la funzione di distribuzione cumulativa. Essa indica la probabilità che una certa variabile assuma un valore inferiore o uguale a un determinato numero.

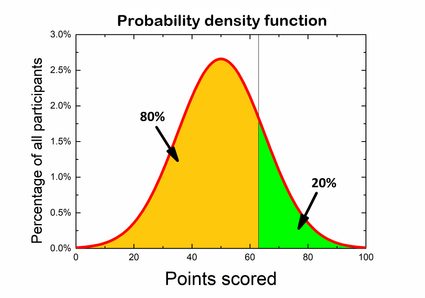
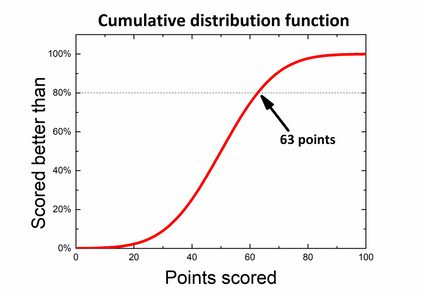
Supponiamo che tu partecipi a un quiz di cultura generale. Il concorso consiste in 100 domande e si guadagna 1 punto per una risposta corretta, mentre per quella sbagliata non ci sono punti. Molte persone hanno già terminato il concorso e dai risultati possiamo ottenere una distribuzione di probabilità. Il regolamento prevede che solo il 20% dei migliori partecipanti venga premiato, quindi ti chiedi quanto dovresti ottenere per essere uno dei vincitori. Se osservi il grafico, puoi dividerlo in modo che l'80% dell'area sottostante si trovi sul lato sinistro e il 20% dei risultati si trovi a destra del punteggio desiderato. Quello che stai cercando è un valore p all'unilaterale sinistro.

Tuttavia, c'è anche un altro modo per trovarlo se utilizziamo una funzione di distribuzione cumulativa — basta trovare il valore 80% sull'asse delle ascisse e il numero di punti corrispondente senza calcolare nulla!

Quasi tutti gli esempi sopra descritti tengono conto della probabilità teorica. Sorge quindi una domanda — qual è la differenza tra probabilità teorica e empirica (nota anche come sperimentale)? La definizione formale di probabilità teorica è il rapporto tra il numero di risultati favorevoli e il numero di tutti i risultati possibili. Si basa sulle informazioni fornite, sul ragionamento logico e ci dice cosa dovremmo aspettarci da un esperimento.

Guarda ancora una volta i sacchetti con le biglie colorate. Ci sono 42 biglie in totale e 18 di queste sono arancioni. Il gioco consiste nel prendere una biglia a caso dal sacchetto e rimetterla a posto, quindi ci sono sempre 42 biglie all'interno. Applicando la definizione di probabilità, possiamo stimare rapidamente 18/42, o semplificando la frazione, 3/7. Ciò significa che se raccogliamo 14 biglie, dovrebbero essercene 6 arancioni.

D'altra parte, la probabilità empirica ci dice esattamente cosa è successo quando abbiamo eseguito un esperimento invece di cosa dovrebbe succedere. Si basa sul rapporto tra il numero di prove riuscite e il numero di tutte le prove. Rimaniamo sullo stesso esempio — prendi una biglia a caso dal sacchetto e ripeti la procedura altre 13 volte. Supponiamo di ottenere 8 biglie arancioni in 14 prove. Questo risultato significa che la probabilità empirica è di 8/14 o 4/7.

Come puoi vedere, il tuo risultato differisce da quello teorico. Non c'è nulla di strano perché se provi a ripetere questo gioco più volte, a volte otterrai un numero maggiore di biglie, a volte un numero minore e a volte otterrai esattamente il numero previsto teoricamente. Se sommi tutti i risultati, dovresti notare che la probabilità complessiva si avvicina sempre di più alla probabilità teorica. In caso contrario, possiamo sospettare che la scelta di una biglia dal sacchetto non sia del tutto casuale — ad esempio, le biglie di colore diverso hanno dimensioni diverse, quindi puoi distinguerle senza doverle guardare.

📚​​ Praticare con tanti esempi e esercizi di probabilità ti aiuteranno a sviluppare le competenze con questi calcoli! 💯

Sia la statistica sia la probabilità sono rami della matematica e si occupano della relazione tra il verificarsi di eventi. Tuttavia, tutti dovrebbero essere consapevoli delle differenze che le rendono due aree distinte.

• La probabilità è generalmente un campo teorico della matematica e indaga le conseguenze delle definizioni e dei teoremi matematici. Al contrario, la statistica è generalmente un'applicazione pratica della matematica nelle situazioni quotidiane e cerca di attribuire senso e comprensione alle osservazioni nel mondo reale.

• La probabilità prevede la possibilità che gli eventi si verifichino, mentre la statistica è fondamentalmente l'analisi della frequenza con cui si sono verificati in passato e crea un modello basato sulle conoscenze acquisite.

• Immagina un probabilista che gioca una partita a carte, che si basa sulla scelta di una carta casuale dall'intero mazzo, sapendo che solo le picche vincono con un rapporto di probabilità predefinito. Supponendo che il mazzo sia completo e che la scelta sia del tutto casuale ed equa, deduce che la probabilità è uguale a ¼ e può fare una scommessa.

• Uno statistico osserverà prima il gioco per un po' di tempo per verificare se, effettivamente, il gioco è equo. Dopo aver verificato (con un'approssimazione accettabile) che vale la pena giocare, chiederà al probabilista cosa dovrebbe fare per vincere di più.

Avrai sicuramente visto alcuni sondaggi sulle preferenze elettorali e ti sarai chiesto come possano essere così precisi rispetto ai punteggi finali, anche se il numero di persone interpellate è di gran lunga inferiore alla popolazione totale — questo è il momento in cui si effettua un campionamento per probabilità.

L'ipotesi di fondo, che è l'idea di base del campionamento, è che i volontari vengano scelti in modo casuale con una probabilità definita in precedenza. Possiamo distinguere tra diversi tipi di metodi di campionamento:

• Campionamento casuale semplice;
• Campionamento casuale a grappoli;
• Campionamento sistematico;
• Campionamento proporzionale alla probabilità;
• Campionamento casuale stratificato;
• Campionamento Minimax;
• Campionamento accidentale;
• Campionamento per quote;
• Campionamento volontario;
• Campionamento panel;
• Campionamento a valanga;
• Campionamento ad intercettazioni lineari; e
• Campionamento teorico.

Ciascuno di questi metodi presenta vantaggi e svantaggi, ma la maggior parte di esse è esaustivo. I vantaggi significativi del campionamento probabilistico sono il risparmio di tempo e l'efficacia dei costi, dato che è necessario intervistare un numero limitato di persone. La semplicità di questa procedura non richiede alcuna competenza e può essere eseguita senza una preparazione approfondita.

Come avrai già capito, ci sono molte aree in cui la teoria della probabilità è applicabile. La maggior parte di essi sono giochi con un elevato fattore di casualità, come la probabilità del lancio di dadi o la scelta di una pallina colorata tra 10 colori diversi, o molti giochi di carte. Le lotterie e il gioco d'azzardo sono i tipi di giochi che sfruttano ampiamente il concetto di probabilità e la generale mancanza di conoscenza in materia. Ovviamente, di tanto in tanto qualcuno vince, ma la probabilità che si tratti di te è estremamente bassa.

La teoria delle probabilità viene utilizzata anche in molti tipi di problemi. Soprattutto quando si parla di investimenti, vale la pena considerare anche il rischio per scegliere l'opzione più appropriata.

Il nostro calcolatore per il bianco natale 🇺🇸 utilizza i dati storici e la conoscenza delle probabilità per prevedere la presenza di neve in varie città durante il periodo natalizio.