Calcolatore per il Test t

Eccoti nel nostro calcolatore per il test t!
Qui non solo puoi eseguire facilmente test a campione unico, ma anche test a due campioni e test a campioni accoppiati.
Preferisci trovare il valore p del test t o preferisci trovare i valori critici del test t? Questo calcolatore per il test t è in grado di fare entrambe le cose! 😊

Cosa ti dice il test t? Dai un'occhiata al testo qui sotto, dove ti spieghiamo cosa viene effettivamente testato quando vengono eseguiti vari tipi di test t. Inoltre, ti spieghiamo quando usare i test t (in particolare se usare il test z o il test t) e quali sono i presupposti che i tuoi dati devono soddisfare affinché i risultati di un test t siano validi. Se hai sempre voluto sapere come fare un test t a mano, ti forniamo la formula del test t necessaria e ti spieghiamo come determinare il numero di gradi di libertà in un test t.

Il test t è uno dei più diffusi test statistici di localizzazione, ovvero si occupa del valore medio della popolazione.
Esistono diversi tipi di test t che si possono eseguire:

• Il test t a campione unico;
• Il test t a due campioni; e
• Il test t a campioni accoppiati.

Nella sezione successiva spiegheremo quando utilizzare un test t specifico.
Ricorda che un test t può essere utilizzato solo per uno o due gruppi. Se devi confrontare tre (o più) medie, usa il metodo dell'analisi della varianza (ANOVA).

Il test t è un test parametrico, il che significa che i tuoi dati devono soddisfare alcuni presupposti:

• I punti dati sono indipendenti; e
• I dati, almeno approssimativamente, seguono una distribuzione normale.

Se il tuo campione non soddisfa questi presupposti, puoi ricorrere ad alternative non parametriche. Visita il nostro calcolatore per il test U di Mann-Whitney 🇺🇸 o il calcolatore per il test di Wilcoxon rank-sum 🇺🇸 per saperne di più. Altre possibilità sono il test di Wilcoxon signed-rank o il test del segno.

La scelta del test t dipende se stai studiando uno o due gruppi:

• Test a campione unico

  Scegli il test t a campione unico per verificare se la media di una popolazione è uguale a un valore ipotizzato in precedenza.

  Esempi:

  • Il volume medio di una bevanda venduta in lattine da 0,33 l — è davvero uguale a 330 ml?
  • Il peso medio delle persone di una determinata città — è diverso dalla media nazionale?

• Test a due campioni

  Scegli il test t a due campioni per verificare se la differenza tra le medie di due popolazioni è uguale a un valore predeterminato, quando i due campioni sono stati scelti indipendentemente l'uno dall'altro.

  In particolare, puoi usare questo test per verificare se i due gruppi sono diversi tra loro.

  Esempi:

  • La differenza media nell'aumento di peso di due gruppi di persone — un gruppo seguiva una dieta ricca di carboidrati e l'altro una dieta ricca di grassi.
  • La differenza media nei risultati di un test di matematica di studenti di due università diverse.

  Questo test viene talvolta definito come test a campioni indipendenti o test a campioni non accoppiati.

• Test a campioni accoppiati

  Il test t a campioni accoppiati viene utilizzato per studiare la variazione della media di una popolazione prima e dopo un intervento sperimentale, sulla base di uno dei campioni, cioè quando ogni soggetto è stato misurato due volte — prima e dopo il trattamento.

  In particolare, puoi usare questo test per verificare se, in media, il trattamento ha avuto effetto sulla popolazione.

  Esempi:

  • Il cambiamento nel rendimento degli studenti prima e dopo aver seguito un corso.
  • La variazione della pressione sanguigna nei pazienti prima e dopo la somministrazione di un farmaco.

Quindi, hai deciso quale test t eseguire. I prossimi passi ti spiegheranno come calcolare il valore p del test t o i suoi valori critici e poi quale decisione prendere riguardo all'ipotesi nulla.

1. Decidi l'ipotesi alternativa:

   • Usa un test t bilaterale se ti interessa solo sapere se la media della popolazione (o, nel caso di due popolazioni, la differenza tra le medie delle popolazioni) è in accordo o in disaccordo con il valore prestabilito.

   • Usa un test t unilaterale se vuoi verificare se la media (o la differenza tra le medie) è maggiore o minore del valore prestabilito.

2. Calcola il valore del punteggio T:

   Le formule per la statistica di prova nei test t includono la dimensione del campione, così come la media e la deviazione standard. La formula esatta dipende dal tipo di test t — per maggiori dettagli, consulta le sezioni dedicate a ciascun test.

3. Determina i gradi di libertà del test t:

   I gradi di libertà sono il numero di osservazioni di campione unico che sono libere di variare durante la stima dei parametri statistici. Nel caso più semplice, il numero di gradi di libertà è uguale alla dimensione del campione meno il numero di parametri da stimare. Anche in questo caso, la formula esatta dipende dal test t che vuoi eseguire — consulta le sezioni seguenti per maggiori dettagli.

I gradi di libertà sono essenziali, in quanto determinano la distribuzione seguita dal punteggio T (sotto l'ipotesi nulla). Se ci sono d gradi di libertà, la distribuzione delle statistiche del test è la distribuzione di Student con d gradi di libertà. Questa distribuzione ha una forma simile a N(0,1) (a campana e simmetrica) ma ha laterali più pesanti. Se il numero di gradi di libertà è elevato (>30), cosa che generalmente accade per i campioni di grandi dimensioni, la distribuzione t di Student è praticamente indistinguibile da N(0,1).

Ricordiamo che il valore p è la probabilità (calcolata sotto l'ipotesi nulla) che la statistica del test produca valori almeno altrettanto estremi del punteggio T prodotto per il tuo campione. Poiché le probabilità corrispondono ad aree sotto la funzione di densità, il valore p del test t può essere illustrato con l'aiuto delle seguenti immagini:

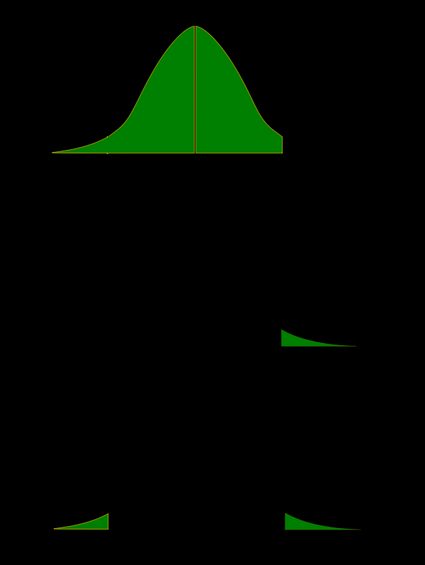
Le seguenti formule indicano come calcolare il valore p del test t. Con cdf_t,d indichiamo la funzione di distribuzione cumulativa della distribuzione t di Student con d gradi di libertà:

1. Valore p del test unilaterale sinistro:

   valore p = cdf_t,d(T_punteggio);

2. Valore p dal test unilaterale destro:

   valore p = 1 - cdf_t,d(T_punteggio); e

3. Valore p dal test bilaterale:

   valore p = 2 × cdf_t,d(-|T_punteggio|),

   o, equivalentemente: valore p = 2 - 2 × cdf_t,d(|T_punteggio|).

Tuttavia, la cdf della distribuzione t è data da una formula un po' complicata. Per trovare il valore p a mano, dovresti ricorrere a tabelle statistiche, dove sono raccolti i valori approssimativi della cdf, o a software statistici specializzati. Fortunatamente, il nostro calcolatore per il test t determina il valore p del test t in un batter d'occhio!

Ricordiamo che nell'approccio ai valori critici dei test di ipotesi, è necessario impostare un livello di significatività, α, prima di calcolare i valori critici, che a loro volta danno origine a regioni critiche (ovvero regioni di rifiuto).

Le formule per i valori critici utilizzano la funzione quadratile della distribuzione t, ovvero l'inverso della cdf:

1. Valore critico per il test t unilaterale sinistro:
   cdf_t,d^-1(α)

   regione critica:

   (-∞, cdf_t,d^-1(α)];

2. Valore critico per il test t unilaterale destro:
   cdf_t,d^-1(1-α)

   regione critica:

   [cdf_t,d^-1(1-α), ∞); e

3. Valori critici per il test t bilaterale:
   ±cdf_t,d^-1(1-α/2)

   regione critica:

   (-∞, -cdf_t,d^-1(1-α/2)] ∪ [cdf_t,d^-1(1-α/2), ∞).

Per decidere il destino dell'ipotesi nulla, basta verificare se il punteggio T rientra nella regione critica:

• Se il tuo punteggio T rientra nella regione critica, rifiuta l'ipotesi nulla e accetta l'ipotesi alternativa.

• Se il tuo punteggio T è al di fuori della regione critica, allora non hai prove sufficienti per rifiutare l'ipotesi nulla.

1. Scegli il tipo di test t che vuoi eseguire:

   • Un test t a campione unico (per verificare la media di un singolo gruppo rispetto a una media ipotizzata);
   • Un test t a due campioni (per confrontare le medie di due gruppi); oppure
   • Un test t a campioni accoppiati (per verificare come cambia la media di uno stesso gruppo dopo un intervento).

2. Decidi l'ipotesi alternativa:

   • Bilaterale;
   • Unilaterale sinistra; o
   • Unilaterale destra;

3. Questo calcolatore per test t ti permette di utilizzare l'approccio del valore p o l'approccio delle regioni critiche ai test di ipotesi!

4. Inserisci il punteggio T e il numero di gradi di libertà. Se non li conosci, fornisci alcuni dati relativi al tuo campione (o ai tuoi campioni) — dimensione del campione, media e deviazione standard e il nostro calcolatore per il test t calcolerà il punteggio T e i gradi di libertà per te.

5. Una volta che tutti i parametri sono presenti, il valore p, o regione critica, apparirà immediatamente sotto il calcolatore per il test t, insieme a un'interpretazione!

1. L'ipotesi nulla è che la media della popolazione sia uguale a un valore $\mu_0$; e

2. L'ipotesi alternativa è che la media della popolazione sia:

   • Diversa da $\mu_0$;
   • Inferiore a $\mu_0$; o
   • Maggiore di $\mu_0$.

Formula del test t a campione unico:

dove:

• $\mu_0$ — Media postulata nell'ipotesi nulla;
• $n$ — Dimensione del campione;
• $\bar{x}$ — Media del campione; e
• $s$ — Deviazione standard del campione.

Numero di gradi di libertà nel test t (campione unico) = $n-1$.

1. L'ipotesi nulla è che la differenza effettiva tra le medie di questi gruppi, $\mu_1$ e $\mu_2$, sia uguale a un valore prestabilito, $\Delta$; e

2. L'ipotesi alternativa è che la differenza $\mu_1 - \mu_2$ sia:

   • Diversa da $\Delta$;
   • Inferiore a $\Delta$; o
   • Maggiore di $\Delta$.

In particolare, se questa differenza predeterminata è pari a zero ($\Delta = 0$):

1. L'ipotesi nulla è che le medie della popolazione siano uguali; e

2. L'ipotesi alternativa è che le medie della popolazione siano uguali:

   • $\mu_1$ e $\mu_2$ sono diverse tra loro;
   • $\mu_1$ è inferiore a $\mu_2$; e
   • $\mu_1$ è maggiore di $\mu_2$.

Formalmente, per eseguire un test t, dobbiamo assumere che le varianze delle due popolazioni siano uguali (questa assunzione è chiamata omogeneità della varianza).

Esiste una versione del test t che può essere applicata senza l'ipotesi di omogeneità della varianza — si tratta del test di Welch. Per comodità, descriviamo entrambe le versioni.

Test t a due campioni se le varianze sono uguali

Usa questo test se sai che le varianze delle due popolazioni sono uguali (o molto simili).

Formula del test t a due campioni (con varianze uguali):

dove $s_p$ è la cosiddetta deviazione standard comune, che calcoliamo come:

e

• $\Delta$ — Differenza media postulata nell'ipotesi nulla;
• $n_1$ — Dimensione del primo campione;
• $\bar{x}_1$ — Media del primo campione;
• $s_1$ — Deviazione standard del primo campione;
• $n_2$ — Dimensione del secondo campione;
• $\bar{x}_2$ — Media del secondo campione; e
• $s_2$ — Deviazione standard del secondo campione.

Numero di gradi di libertà nel test t (due campioni, varianze uguali) = $n_1 + n_2 - 2$.

Test t a due campioni se le varianze sono disuguali (test t di Welch)

Usa questo test se le varianze delle tue popolazioni sono diverse.

Formula del test t di Welch a due campioni se le varianze sono disuguali:

dove:

• $\Delta$ — Differenza media postulata nell'ipotesi nulla;
• $n_1$ — Dimensione del primo campione;
• $\bar{x}_1$ — Media del primo campione
• $s_1$ — Deviazione standard del primo campione;
• $n_2$ — Dimensione del secondo campione;
• $\bar{x}_2$ — Media del secondo campione; e
• $s_2$ — Deviazione standard del secondo campione.

Il numero di gradi di libertà in un test t di Welch (test t a due campioni con varianze disuguali) è molto difficile da calcolare. Possiamo approssimarlo con l'aiuto della seguente formula di Satterthwaite:

In alternativa, puoi prendere il minore tra $n_1 - 1$ e $n_2 - 1$ come stima conservativa del numero di gradi di libertà.

Poiché di solito eseguiamo un test t a campioni accoppiati quando abbiamo dati sugli stessi soggetti misurati due volte (prima e dopo un trattamento), adottiamo la convenzione di riferirci ai campioni come pre-gruppo e post-gruppo.

1. L'ipotesi nulla è che la vera differenza tra le medie delle popolazioni pre e post sia uguale a un valore prestabilito, $\Delta$; e

2. L'ipotesi alternativa è che la differenza reale tra queste medie sia:

   • Diversa da $\Delta$;
   • Inferiore a $\Delta$; o
   • Maggiore di $\Delta$.

In genere, questa differenza predeterminata è pari a zero. Possiamo quindi riformulare le ipotesi come segue:

1. L'ipotesi nulla è che le medie pre e post siano uguali, ovvero che il trattamento non abbia alcun impatto sulla popolazione; e

2. L'ipotesi alternativa:

   • Le medie pre e post sono diverse tra loro (il trattamento ha un qualche effetto);
   • La media pre è inferiore alla media post (il trattamento aumenta il risultato); oppure
   • La media pre è maggiore della media post (il trattamento diminuisce il risultato).

Formula del test t a campioni accoppiati

In effetti, un test t a campioni accoppiati è tecnicamente uguale a un test t a campione unico! Vediamo la spiegazione. Che $x_1, ... , x_n$ sia l'osservazione precedente e che $y_1, ... , y_n$ sia l'osservazione successiva. Cioè, $x_i, y_i$ sono le misurazioni prima e dopo del soggetto i-esimo.

Per ogni soggetto, calcola la differenza, $d_i := x_i - y_i$. Tutto ciò che segue è un semplice test t a campione unico eseguito sul campione di differenze $d_1, ... , d_n$. Dai un'occhiata alla formula del punteggio T:

dove:

• $\Delta$ — Differenza media postulata nell'ipotesi nulla;

• $n$ — Dimensione del campione di differenze, cioè il numero di coppie;

• $\bar{x}$ — Media del campione di differenze; e

• $s$ — Deviazione standard del campione di differenze.

Numero di gradi di libertà nel test t (a campioni accoppiati): $n - 1$.

Utilizziamo il test z quando vogliamo verificare la media della popolazione di un insieme di dati normalmente distribuiti, che hanno una varianza della popolazione nota. Se il numero di gradi di libertà è elevato, la distribuzione t di Student è molto vicina a N(0,1).

Quindi, se ci sono molti punti dati (almeno 30), puoi sostituire il test t con il test z e i risultati saranno quasi identici. Tuttavia, per campioni piccoli con varianza sconosciuta, ricordati di usare il test t perché, in questo caso, la distribuzione t di Student differisce significativamente da quella N(0,1)!