Calcolatore per il Test Z

Questo calcolatore per il test Z è uno strumento che ti aiuta a eseguire un test Z sulla media di una popolazione. Esistono due forme di questo test, il test Z bilaterale e il test Z unilaterale, che possono essere utilizzati a seconda delle tue esigenze. Puoi anche scegliere se il calcolatore deve determinare il valore p dal test Z o se preferisci utilizzare l'approccio del valore critico!

Continua a leggere per saperne di più sui test Z in statistica e, in particolar modo, quando ricorrere al test Z, qual è la formula del test Z e se dovresti usare il test Z o il test t. Come bonus, ti forniamo alcuni esempi con spiegazioni passo a passo su come eseguire il test Z!

In alternativa, puoi anche consultare il nostro calcolatore per la statistica t, dove potrai imparare il concetto di un altro test statistico essenziale. Se ti interessa anche il test F, consulta il nostro calcolatore per il test F 🇺🇸.

Il test Z fatto su un campione è uno dei test di localizzazione più diffusi. L'ipotesi nulla è che il valore medio della popolazione sia uguale a un dato numero, $\mu_0$:

Eseguiamo un test Z bilaterale se vogliamo verificare se la media della popolazione non è $\mu_0$:

E un test Z unilaterale se vogliamo verificare se la media della popolazione è minore o maggiore di $\mu_0$:

Discutiamo ora i presupposti di un test Z su un campione.

Puoi utilizzare il test Z se il tuo campione è composto da punti di dati indipendenti e se:

• I dati sono distribuiti normalmente e conosci la variazione della popolazione;

  oppure se

• Il campione è ampio e i dati seguono una distribuzione che ha una media e una variazione finite. In questo caso, non è necessario conoscere la variazione della popolazione.

Il motivo per cui esistono queste due possibilità è che vogliamo che le statistiche del test seguano la distribuzione normale standard $\mathrm N(0, 1)$. Nel primo caso, si tratta di una distribuzione normale standardizzata esatta, mentre nel secondo caso lo è approssimativamente, grazie al teorema del limite centrale.

Rimane la domanda: "Quando il mio campione può essere considerato grande?" Beh, non esiste un criterio universale. In generale, più punti dati si hanno, meglio funziona l'approssimazione. I libri di statistica consigliano di avere non meno di 50 punti dati, mentre 30 sono considerati il minimo indispensabile.

Sia $x_1, ..., x_n$ un campione indipendente che segue la distribuzione normale $\mathrm N(\mu, \sigma^2)$, cioè con una media pari a $\mu$ e una variazione pari a $\sigma ^2$.

Poniamo l'ipotesi nulla, $\mathrm H_0 \!\!:\!\! \mu = \mu_0$.

Definiamo il test Z:

dove:

• $\bar x$ — Media del campione, cioè $\bar x = (x_1 + ... + x_n) / n$;
• $\mu_0$ — Media postulata in $\mathrm H_0$;
• $n$ — Dimensione del campione; e
• $\sigma$ — Deviazione standard della popolazione.

Nel seguito, il carattere maiuscolo $Z$ significa $\text{test Z}$ (trattato come una variabile aleatoria), mentre il carattere minuscolo $z$ indicherà il valore effettivo di $Z$, calcolato per un dato campione estratto da N(μ,σ²).

Se $\mathrm H_0$ è valido, allora la somma $S_n = x_1 + ... + x_n$ segue la distribuzione normale, con media $n \mu_0$ e variazione $n^2 \sigma$. Poiché $Z$ è la standardizzazione (test Z) di $S_n/n$, possiamo concludere che il test $Z$ segue la distribuzione normale standard $\mathrm N(0, 1)$, a condizione che l'ipotesi $\mathrm H_0$ sia vera. A proposito, abbiamo il calcolatore per il punteggio Z se vuoi concentrarti solo su questo valore.

Se i dati non seguono una distribuzione normale o se la deviazione standard della popolazione non è nota (e quindi nella formula per $Z$ sostituiamo la deviazione standard della popolazione $\sigma$ con la deviazione standard del campione), allora il test statistico $Z$ non è necessariamente normale. Tuttavia, se il campione è sufficientemente grande, il teorema del limite centrale garantisce che $Z$ è approssimativamente $\mathrm N(0, 1)$.

Nelle sezioni seguenti, ti spiegheremo come utilizzare il valore del test statistico, $z$, per decidere se rifiutare o meno l'ipotesi nulla. Per arrivare a questa decisione si possono utilizzare due approcci: l'approccio del valore p e l'approccio del valore critico — e noi li trattiamo entrambi! Quale dei due dovresti usare? In passato, l'approccio del valore critico era più popolare perché era difficile calcolare il valore p dal test Z. Tuttavia, con l'aiuto dei computer moderni, possiamo farlo abbastanza facilmente e con una discreta precisione. In generale, ti consigliamo di riportare il valore p dei tuoi test!

Formalmente, il valore p è il più piccolo livello di significatività al quale l'ipotesi nulla può essere rifiutata. Più intuitivamente, il valore p risponde alla domanda:
Ammesso che io viva in un mondo in cui l'ipotesi nulla è valida, quanto è probabile che il valore del test statistico sia almeno altrettanto estremo del valore $z$ che ho ottenuto per il mio campione? Quindi, un valore p piccolo significa che il tuo risultato è molto improbabile in base all'ipotesi nulla e quindi c'è una forte prova contro l'ipotesi nulla — più piccolo è il valore p, più forte è la prova.

Per trovare il valore p, devi calcolare la probabilità che il test statistico, $Z$, sia almeno altrettanto estremo che il valore effettivamente osservato, $z$, a condizione che l'ipotesi nulla sia vera (la probabilità di un evento calcolata sotto l'ipotesi che $\mathrm H_0$ sia vera sarà indicata come $\small \mathrm{P}(\text{evento} | \mathrm{H_0})$). È l'ipotesi alternativa a determinare il significato di "più estremo":

1. Test Z bilaterale — I valori estremi sono quelli il cui valore assoluto supera $|z|$, quindi quelli inferiori a $-|z|$ o superiori a $|z|$. Pertanto, abbiamo:

La simmetria della distribuzione normale dà:

2. Test Z unilaterale sinistro — I valori estremi sono quelli più piccoli di $z$, quindi

3. Test Z unilaterale destro — I valori estremi sono quelli maggiori di $z$, quindi

Per calcolare queste probabilità, possiamo utilizzare la funzione di ripartizione, chiamata anche funzione cumulativa (CDF, dall'inglese cumulative distribution function, di $\mathrm N(0, 1)$, che per un numero reale, $x$, è definita come:

Inoltre, i valori p possono essere rappresentati come l'area sotto la funzione di densità di probabilità (PDF, dall'inglese probability density function) di $\mathrm N(0, 1)$ perché:

Con tutte le conoscenze acquisite nella sezione precedente, è ora di imparare tutto sui test Z.

1. Test Z bilaterale:

Dal fatto che $\Phi(-z) = 1 - \Phi(z)$, deduciamo che

Il valore p è l'area sotto la funzione di distribuzione di probabilità sia a sinistra di $-|z|$, sia a destra di $|z|$:

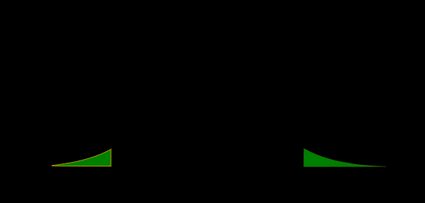
2. Test Z unilaterale sinistro:

Il valore p è l'area sotto la funzione di distribuzione di probabilità a sinistra del nostro valore $z$:

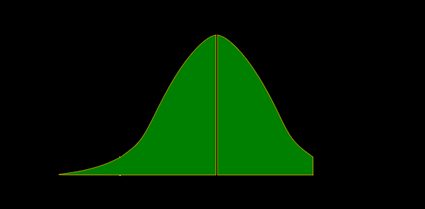
3. Test z unilaterale destro:

Il valore p è l'area sotto la funzione di distribuzione di probabilità a destra di $z$:

La decisione se rifiutare o meno l'ipotesi nulla può essere presa a qualunque livello di significatività, $\alpha$, tu desideri!

• Se il valore p è minore o uguale a $\alpha$, l'ipotesi nulla viene rifiutata a questo livello di significatività; e

• Se il valore p è maggiore di $\alpha$, allora non ci sono prove sufficienti per rifiutare l'ipotesi nulla a questo livello di significatività.

L'approccio del valore critico prevede il confronto del valore del test statistico ottenuto per il nostro campione, $z$, con i cosiddetti valori critici. Questi valori costituiscono i confini delle regioni in cui è altamente improbabile che il test statistico si trovi. Queste regioni vengono spesso chiamate regioni di rifiuto o regioni critiche. La decisione di rifiutare o meno l'ipotesi nulla si basa sul fatto che il nostro $z$ appartenga o meno alla regione critica.

Le regioni critiche dipendono dal livello di significatività, $\alpha$, del test e dall'ipotesi alternativa. La scelta di $\alpha$ è arbitraria; in pratica, i valori di $0,\!1$, $0,\!05$ o $0,\!01$ sono più comunemente utilizzati come $\alpha$.

Una volta concordato il valore di $\alpha$, possiamo facilmente determinare le regioni critiche del test Z:

1. Test Z bilaterale:

2. Test Z unilaterale sinistro:

3. Test Z unilaterale destro:

Per decidere il destino di $\mathrm H_0$, controlla se il tuo $z$ cade o meno nella regione di rifiuto:

• Se sì, allora rifiuta $\mathrm H_0$ e accetta $\mathrm H_1$; e

• Se no, allora non ci sono prove sufficienti per rifiutare $\mathrm H_0$.

Come vedi, le formule per i valori critici di test Z coinvolgono l'inverso, $\Phi^{-1}$, della funzione di ripartizione (CDF) di $\mathrm N(0, 1)$.

Il nostro calcolatore riduce tutti i passaggi complicati:

1. Scegli l'ipotesi alternativa (bilaterale, o unilaterale destro o sinistro);

2. Nel nostro calcolatore per il test Z, puoi decidere se utilizzare il valore p o l'approccio delle regioni di rifiuto. In quest'ultimo caso, imposta il livello di significatività, $\alpha$;

3. Inserisci il valore del test statistico, $z$. Se non lo conosci, puoi inserire alcuni dati che ci permetteranno di calcolare il valore di $z$ per te:

   • La media del campione $\bar x$ (se hai dei dati grezzi, vai al calcolatore per la media per determinare la media),
   • La media testata $\mu_0$,
   • La dimensione del campione $n$, e
   • La deviazione standard della popolazione $\sigma$ (o deviazione standard del campione se il campione è ampio); e infine

4. I risultati verranno visualizzati immediatamente sotto il calcolatore.

Se vuoi trovare $z$ in base al valore p, ricorda che nel caso del test bilaterale ci sono due possibili valori di $z$ — uno positivo e uno negativo, e sono numeri opposti. In questo caso, il calcolatore per il test Z restituisce il valore positivo. Per trovare l'altro possibile valore di $z$ per un dato valore p, basta prendere il numero opposto al valore di $z$ visualizzato dal calcolatore.

Per assicurarci che tu abbia compreso appieno l'essenza del test Z, vediamo alcuni esempi:

1. Una macchina per il riempimento di bottiglie segue una distribuzione normale. La sua deviazione standard, come dichiarato dal produttore, è pari a 30 mL. Un venditore di succhi di frutta afferma che il volume versato in ogni bottiglia è in media di un litro, cioè 1000 mL, ma sospettiamo che in realtà il volume medio sia inferiore al volume dato.

Formalmente, le ipotesi che abbiamo posto sono le seguenti:

• $\mathrm H_0 \! : \mu = 1000 \text{ mL}$

• $\mathrm H_1 \! : \mu \lt 1000 \text{ mL}$

Siamo andati in un negozio e abbiamo acquistato un campione di 9 bottiglie. Dopo aver misurato attentamente il volume di succo in ogni bottiglia, abbiamo ottenuto il seguente campione (in millilitri):

$\small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980$

• Dimensione del campione: $n = 9$;

• Media del campione: $\bar x = 980 \ \mathrm{mL}$; e

• Deviazione standard della popolazione: $\sigma = 30 \ \mathrm{mL}$.

• Quindi

• E dunque $\text{Valore p} = \Phi(-2) \approx 0,\!0228$.

  Come $0,\!0228 \lt 0,\!05$, concludiamo che i nostri sospetti non sono infondati; al livello di significatività più comune, $0,\!05$, rifiutiamo l'affermazione del produttore, $\mathrm H_0$, e accettiamo l'ipotesi alternativa, $\mathrm H_1$.

2. Abbiamo lanciato una moneta 50 volte. Abbiamo ottenuto croce 20 volte e testa 30 volte. Ci sono prove sufficienti per affermare che la probabilità di ottenere croce o testa è distorta?

   Chiaramente i nostri dati seguono la distribuzione di Bernoulli, con una certa probabilità di successo $p$ e una variazione $\sigma^2 = p (1-p)$. Tuttavia, il campione è ampio, quindi possiamo tranquillamente eseguire un test Z. Adottiamo la convenzione secondo cui otteniamo croce.

   Formuliamo l'ipotesi nulla e l'ipotesi alternativa:

   • $\mathrm H_0 \! : p = 0,\!5$. (La moneta è equa — la probabilità di ottenere croce è di $0,\!5$); e

   • $\mathrm H_1 \! : p \ne 0,\!5$. (La moneta è distorta — la probabilità di ottenere croce è diversa da $0,\!5$).

   Nel nostro campione abbiamo 20 successi (indicati con $1$) e 30 fallimenti (indicati con $0$), quindi:

• Dimensione del campione $n = 50$;

• Media del campione $\bar x = 20/50 = 0,\!4$; e

• La deviazione standard della popolazione è data da $\sigma = \sqrt{0,\!5 \times 0,\!5}$ (perché $0,\!5$ è la proporzione $p$ ipotizzata in $\mathrm H_0$). Quindi, $\sigma = 0,\!5$;

• Dunque:

• E pertanto:

Dal momento che $0,\!1573 \gt 0,\!1$, non abbiamo prove sufficienti per rifiutare l'affermazione che la probabilità di ottenere testa o croce è regolare, anche a un livello di significatività così alto — $0,11$. In questo caso, puoi tranquillamente donare un soldo al tuo Witcher o utilizzare il calcolatore per il lancio della moneta per trovare le probabilità di ottenere, ad esempio, 10 teste di fila (che sono estremamente basse!).