Calcolatore del Coefficiente Angolare

Il calcolatore del coefficiente angolare determina la pendenza o il gradiente tra due punti nel sistema di coordinate Cartesiane. Il coefficiente angolare esprime la quantità di inclinazione di una linea e può avere un valore positivo, negativo, nullo o indefinito. Prima di usare il calcolatore, probabilmente vale la pena imparare a trovare il coefficiente angolare usando la formula del coefficiente angolare. Per trovare l'equazione di una retta per due punti qualsiasi che la attraversano, usa il nostro calcolatore per la forma esplicita dell'equazione di una retta.

Qui di seguito ti spiegheremo come si usa questo calcolatore, con un esempio di calcolo, per renderti le cose più semplici. Per calcolare la pendenza di una retta, devi conoscere due punti qualsiasi su di essa:

1. Inserisci le coordinate x e y del primo punto della retta.

2. Inserisci le coordinate x e y del secondo punto della retta.

3. Otterremo immediatamente il coefficiente angolare. Ma la magia non si ferma qui, perché otterrai anche una serie di risultati extra:

   • L'equazione della funzione (uguale all'equazione della retta).
   • L'intersezione con l'asse y.
   • L'angolo che la retta forma rispetto all'asse x (antiorario).
   • La pendenza come percentuale (grado percentuale).
   • La distanza tra i due punti.

Per esempio, supponiamo di avere una linea che passa per i punti (1, 5) e (7, 6). Inserisci le coordinate x e y del primo punto, seguite dalle coordinate x e y del secondo. Immediatamente apprendiamo che la pendenza della retta è 0,166667. Se abbiamo bisogno dell'equazione della retta, ora l'abbiamo anche: y = 0,16667x + 4,83333.

Puoi usare questo calcolatore al contrario e trovare una coordinata x o y mancante! Ad esempio, considera la linea che passa per il punto (9, 12) e ha una pendenza del 12%. Per trovare il punto in cui la retta incrocia l'asse y (cioè x = 0), inserisci 12% in percentuale (9, 12) come coordinata del primo punto e x₂ = 0. Immediatamente, il calcolatore ci dice che y₂ = 10,92.

Il coefficiente angolare di una retta ha molti usi significativi in geometria e in calcolo. L'articolo che segue è un'eccellente introduzione ai fondamenti di questo argomento e ti invitiamo a leggerlo.

Nota che il coefficiente angolare di una retta è facilmente calcolabile a mano utilizzando coordinate piccole e con numeri interi. La formula diventa sempre più utile quando le coordinate assumono valori più grandi o decimali.

Se la retta che contiene i due punti è data un'equazione in forma

$y = m x + c$

allora il coefficiente angolare è uguale a $m$, mentre $c$ è la coordinata verticale dell'intercetta.

Vale la pena ricordare che qualsiasi retta orizzontale ha un coefficiente angolare pari a zero perché una retta orizzontale ha le stesse coordinate y. Questo si traduce in uno zero nel numeratore della formula del coefficiente angolare. D'altra parte, una linea verticale avrà un coefficiente angolare indefinito poiché le coordinate x saranno sempre le stesse. Questo comporterà un errore di divisione per zero quando si utilizza la formula.

1. Identifica le coordinate $(x_1, y_1)$ e $(x_2, y_2)$. Utilizzeremo la formula per calcolatore del coefficiente angolare della retta passante per i punti $(3, 8)$ e $(-2, 10)$;
2. Inserisci i valori nella formula. Otteniamo così $(10 - 8)/(-2 - 3)$;
3. Sottrai i valori tra parentesi per ottenere $2/(-5)$;
4. Semplifica la frazione per ottenere il coefficiente angolare di $-2/5$; e
5. Verifica il risultato utilizzando il calcolatore del coefficiente angolare.

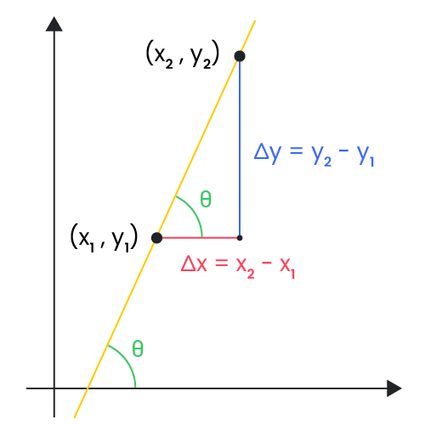
Per trovare il coefficiente angolare di una retta, abbiamo bisogno di due coordinate sulla retta. Saranno sufficienti due coordinate qualsiasi. In pratica stiamo misurando la variazione della coordinata y, spesso nota come ascissa, divisa per la variazione della coordinata x, nota come ordinata. I calcoli per trovare il coefficiente angolare sono semplici e non comportano altro che sottrazioni e divisioni di base.

Intuitivamente, la pendenza di una retta rappresenta il tasso di variazione della funzione. Uno degli esempi più semplici della pendenza di una retta nella vita reale è la velocità: la misura di come la posizione cambia nel tempo.

Supponiamo che un ciclista viaggi lungo una linea retta e che la sua posizione al tempo t rispetto al punto iniziale 0 sia data dalla formula x(t) = 5t + 3. (Attenzione: qui la posizione varia con il tempo, quindi x è una funzione di t, a differenza delle sezioni precedenti in cui abbiamo variato y rispetto a x) Quindi, la loro velocità è v = 5, che è esattamente la pendenza nella formula di x(t). La sua interpretazione fisica è che in un incremento di tempo Δt, il ciclista copre una distanza di 5(Δt).

Nell'esempio precedente, il ciclista viaggiava a velocità costante (v = 5). Ma cosa succede se invece rendiamo l'accelerazione costante? Supponiamo che il ciclista inizi la sua corsa nel punto x = 0 con velocità zero e accelerazione a = 10. Ciò significa che partendo da 0, il ciclista aumenta la sua velocità di 10 in ogni unità di tempo e quindi la sua velocità al tempo t è v(t) = 10t. Proprio come la velocità è il tasso di variazione della posizione, l'accelerazione è il tasso di variazione della velocità, quindi l'accelerazione deriva dalla formula di velocità.

E la posizione del ciclista in questo caso? Si scopre che la sua posizione è descritta dalla formula x(t) = 5t². Spiegheremo più avanti da dove deriva questa formula: per ora, il punto importante è che in un moto con accelerazione costante, la posizione è una funzione quadratica del tempo (anziché lineare, come nel caso del moto a velocità costante). Di conseguenza, la velocità non è più data da una singola formula. Questa è una conseguenza del fatto che la velocità non è più costante, dunque, il tasso di variazione dato da una funzione è un valore fisso solo se la funzione è lineare.

Come possiamo quindi calcolare la velocità v(t) = 10t dalla formula di posizione x(t) = 5t²? Dobbiamo differenziare x(t) (cioè prendere la sua derivata). La derivata di una funzione in un determinato momento è proprio il suo tasso di variazione in quel momento; pertanto, v(t) è la derivata di x(t), indicata come x'(t) o dx(t)/dt.

In termini geometrici, la derivata x'(t) è il coefficiente lineare della retta tangente alla funzione al tempo t; in generale, ad ogni tempo t, la retta tangente sarà diversa, e così anche la derivata. Quindi, la differenziazione perfeziona l'idea di calcolare il coefficiente angolare, in quanto ci permette di calcolare il coefficiente di funzioni il cui tasso di variazione varia anch'esso.

Il contrario della differenziazione è l'integrazione: il processo in cui si calcola una funzione a partire dalla sua derivata. È attraverso l'integrazione che otteniamo la funzione di posizione del ciclista x(t) = 5t² dalla sua velocità v(t) = 10t. Geometricamente, integrare una funzione equivale a calcolare l'area sotto la funzione. Il grafico della funzione velocità v(t) = 10t determina un triangolo con base t e altezza 10t, quindi l'area sotto il grafico è 0,5 × t × (10t) = 5t² — è esattamente la nostra funzione di posizione!

Così come il coefficiente angolare può essere calcolata utilizzando gli estremi di un segmento, anche il punto medio può essere calcolato. Il punto medio è un concetto importante in geometria, in particolare quando si inscrive un poligono all'interno di un altro poligono i cui vertici toccano il punto medio dei lati del poligono più grande. Il punto medio può essere ottenuto utilizzando il calcolatore per il punto medio o semplicemente prendendo la media di ogni ordinata e la media delle ascisse per formare una nuova coordinata.

Le pendenze delle linee sono importanti per determinare se un triangolo è un triangolo rettangolo o meno. Se due lati di un triangolo hanno pendenze che si moltiplicano fino a diventare uguali a -1, allora il triangolo è un triangolo rettangolo. I calcoli per questo possono essere fatti a mano o utilizzando il calcolatore per triangoli rettangoli. Puoi anche utilizzare il calcolatore per le distanze per calcolare quale lato di un triangolo è il più lungo, il che aiuta a determinare quali lati devono formare un angolo retto se il triangolo è retto.

Il segno davanti al coefficiente angolare fornito dal calcolatore del coefficiente angolare indica se la linea è crescente, decrescente, costante o indefinita. Se il grafico della retta si muove dal basso a sinistra all'alto a destra, è crescente e quindi positivo. Se diminuisce quando si sposta dall’alto a sinistra a basso a destra, allora il coefficiente angolare è negativo.

Il calcolatore del coefficiente angolare è uno dei più vecchi di Omni Calculator, costruito dai nostri veterani Mateusz e Julia, che fanno sembrare facile la creazione di precisi strumenti scientifici. L'idea di questo calcolatore è nata quando i due stavano calcolando dati analitici e tendenze e si sono resi conto di come una calcolatore del coefficiente angolare avrebbe facilitato il loro lavoro. Ancora oggi, puoi trovarli occasionalmente ad utilizzare questo strumento per effettuare calcoli affidabili.

Prestiamo molta attenzione alla qualità dei nostri contenuti, affinché siano il più precisi e affidabili possibile. Ogni strumento viene revisionato da un esperto e poi corretto da un madrelingua. Puoi scoprire di più sui nostri standard nella nostra pagina Politiche Editoriali.