Calcolatore per la Forma dell'Intercetta della Pendenza

Il calcolatore per le formule di intercetta della pendenza ti insegnerà come trovare l'equazione di una retta a partire da due punti qualsiasi per cui passa la retta. Ti aiuterà a trovare i coefficienti della pendenza e dell'intercetta y, così come l'intercetta x, utilizzando le formule dell'intercetta della pendenza. Continua a leggere per scoprire cos'è la forma dell'intercetta della pendenza di un'equazione lineare, come trovare l'equazione di una retta e l'importanza della forma dell'intercetta della pendenza nella vita reale.

Qualsiasi linea su un piano può essere descritta matematicamente come una relazione tra le posizioni verticali (asse y) e orizzontali (asse x) di ciascuno dei punti che contribuiscono alla linea. Questa relazione può essere scritta come y = [qualcosa con x]. La forma specifica di [qualcosa con x] determinerà il tipo di retta che abbiamo. Ad esempio, y = x² + x è una parabola, chiamata anche funzione quadratica. D'altra parte, y = mx + b (con m e b che rappresentano qualsiasi numero reale) è la relazione di una linea retta.

In questo calcolatore per la forma dell'intercetta della pendenza, ci concentreremo solo sulla linea retta. Puoi consultare il nostro calcolatore del tasso di variazione medio per trovare la relazione tra le variabili di funzioni non lineari.

Le equazioni lineari, o equazioni della retta, possono essere riconosciute rapidamente perché non hanno termini con esponenti. (Ad esempio, troverai una x o una y, ma mai una x²). Ogni equazione lineare descrive una linea retta, che può essere espressa utilizzando la forma di equazione intercetta-pendenza.

Come abbiamo visto in precedenza, è possibile scrivere l'equazione di qualsiasi retta nella forma y = mx + b. Questa è la cosiddetta forma pendenza-intercetta perché fornisce due importanti informazioni — la pendenza m e l'intercetta b della retta. Potrai utilizzare questi valori per l'interpolazione lineare in seguito.

Il termine pendenza è l'inclinazione, o pendenza, di una retta. Ci dice di quanto cambia y per una variazione fissa di x. Se è positiva, i valori di y aumentano quando x aumenta. Se è negativo, y diminuisce all'aumentare di x. Puoi trovare maggiori informazioni nella descrizione del nostro calcolatore per la pendenza.

L'intercetta y è il valore di y in corrispondenza del quale la retta incrocia l'asse delle y. Per trovarla, devi sostituire x = 0 all'equazione lineare. Vedrai più avanti perché l'intercetta y è un parametro importante nelle equazioni lineari e imparerai anche il significato fisico del suo valore in alcuni esempi reali.

Hai ancora bisogno di sapere come trovare l'intercetta della pendenza di un'equazione lineare? Supponiamo che si conoscano due punti attraversati dalla retta. Il primo avrà coordinate (x₁, y₁) e il secondo (x₂, y₂). Le incognite sono la pendenza m e l'intercetta b.

Per prima cosa, sostituisci le coordinate dei due punti nell'equazione dell'intercetta della pendenza:

(1) y₁ = mx₁ + b; e

(2) y₂ = mx₂ + b.

Quindi, sottrai la prima equazione dalla seconda:

y₂ - y₁ = m(x₂ - x₁).

Infine, dividi entrambi i lati dell'equazione per (x₂ - x₁) per trovare la pendenza:

m = (y₂ - y₁)/(x₂ - x₁).

Una volta trovata la pendenza, puoi sostituirla alla prima o alla seconda equazione per trovare l'intercetta y:

y₁ = x₁(y₂ - y₁)/(x₂ - x₁) + b; e

b = y₁ - x₁(y₂ - y₁)/(x₂ - x₁).

Questo calcolatore per la forma dell'intercetta della pendenza ti permette di trovare l'equazione di una retta nella forma dell'intercetta della pendenza. Tutto ciò che devi fare è indicare due punti attraversati dalla retta. Devi seguire la procedura descritta di seguito:

1. Scrivi le coordinate del primo punto. Supponiamo che sia un punto con x₁ = 1 e y₁ = 1;

2. Scrivi anche le coordinate del secondo punto. Prendiamo un punto con x₂ = 2 e y₂ = 3;

3. Usa la formula dell'intercetta della pendenza per trovare la pendenza:

   m = (y₂ - y₁)/(x₂ - x₁) = (3-1)/(2-1) = 2/1 = 2;

4. Calcola l'intercetta y. Puoi anche utilizzare x₂ e y₂ al posto di x₁ e y₁.

   b = y₁ - m × x₁ = 1 - 2×1 = -1;

5. Metti insieme tutti questi valori per costruire la forma dell'intercetta della pendenza di un'equazione lineare:

   y = 2x - 1; e

6. Puoi anche utilizzare il calcolatore per la distanza per trovare la distanza tra due punti.

È anche sempre possibile trovare l'intercetta x di una retta. Si tratta del valore di x in corrispondenza del quale la retta incrocia l'asse x (significa il valore di x per il quale y è uguale a 0). Puoi calcolarla nel seguente modo:

0 = mx + b;

x = -b/m.

Come possiamo vedere, l'unica condizione che deve essere soddisfatta è che il coefficiente m sia diverso da zero.

Il nostro calcolatore per la forma dell'intercetta della pendenza visualizzerà i valori dell'intercetta x e dell'intercetta y per te. Tuttavia, se vuoi saperne di più, ti consigliamo di visitare il nostro calcolatore per l'intercetta di x e y 🇺🇸.

Abbiamo già visto cos'è la forma dell'intercetta della pendenza, ma per capire perché l'equazione della forma dell'intercetta della pendenza è così utile, dovresti conoscere alcune applicazioni che ha nel mondo reale. Vediamo un paio di esempi. Inizieremo con dei semplici esempi tratti dalla fisica in modo che tu possa avere un'idea intuitiva di cosa significhino l'intercetta y e l'intercetta x.

Immagina un'auto che si muove a velocità costante verso di te. Il suo movimento può essere tracciato come tempo rispetto alla distanza dell'auto da te (come mostrato sopra). Ciò significa che l'asse delle ascisse rappresenterà il tempo trascorso e l'asse delle ordinate rappresenterà la distanza dall'auto. Puoi anche immaginare che l'auto abbia iniziato a muoversi prima che tu avviassi il timer (cioè prima di t = 0).

Ora, se guardi l'intercetta y (x = 0), il punto in cui hai iniziato a tenere traccia del tempo è t = 0. Quindi, il valore di y in questo punto indicherà la posizione (distanza) iniziale dell'auto rispetto a te. Questo valore è, come abbiamo già detto, lo stesso valore di b nella forma di intercetta della pendenza di un'equazione della retta.

Guardando ora l'intercetta x (y = 0), questo sarà il punto in cui la distanza dell'auto da te sarà 0. Quindi il valore di x in questo punto sarà il momento in cui tu e l'auto eravate nello stesso posto. Speriamo che questo significhi che eri all'interno dell'auto e non sotto.

L'esempio dell'auto qui sopra è molto semplice e dovrebbe aiutarti a capire perché la forma pendenza-intercetta è importante e, più in particolare, il significato delle intercette. In questo articolo parleremo principalmente di linee rette, ma i punti di intercetta possono essere calcolati per qualsiasi tipo di curva (se attraversa u'asse).

Infatti, l'esempio precedente non corrisponde a un'equazione lineare e presenta comunque entrambe le intercette. Lo stesso vale per qualsiasi altra parabola o altra forma.

Un'equazione che garantisce un'intercetta y ma non necessariamente un'intercetta x è la parabola. Questa equazione è mostrata nell'immagine qui sopra. Ha un massimo o un minimo (a seconda dell'orientamento). Se il massimo è sotto l'asse x o il minimo è sopra l'asse x, non ci sarà mai un'intercetta x.

Tuttavia, a differenza degli esseri umani, non tutte le equazioni sono uguali. Alcune formule descrivono curve che potrebbero non intercettare mai l'asse x, l'asse y o entrambi. Vediamo un po' più nel dettaglio come questo può accadere.

Possiamo distinguere 3 gruppi di equazioni a seconda che abbiano solo l'intercetta y, solo l'intercetta x o nessuna. Il primo gruppo (solo l'intercetta y) può avere quasi tutti i tipi di equazioni, comprese quelle lineari. Un buon esempio semplice è y = 3 (o qualsiasi altro valore costante di y ad eccezione di 0) poiché si tratta di una retta parallela all'asse x e quindi non la attraverserà né la intercetterà mai. Non cercare di calcolare questo tipo di intercettazioni con questo calcolatore per la forma dell'intercetta della pendenza perché questo tipo di equazioni può potenzialmente rompere l'Internet.

Il secondo e il terzo gruppo di equazioni sono un po' più complicati da immaginare e per capirli bene dobbiamo introdurre il concetto di asintoto. Un asintoto è una linea (che può essere espressa come un'equazione lineare) alla quale la funzione o la curva di cui stiamo parlando si avvicina sempre di più, senza però mai attraversarla o toccarla.

La definizione potrebbe non sembrare del tutto chiara, ma se osserviamo un esempio di equazione, avremo meno problemi di comprensione. Prendiamo l'equazione y = 1/x. Se proviamo a trovare l'intercetta y sostituendo x = 0, otterremo quella che viene definita un'espressione matematicamente indefinita poiché non ha senso dividere per 0.

Se prendiamo valori sempre più vicini a 0 (qualcosa come 0,1, poi 0,001, 0,000001...), possiamo vedere che il valore di y aumenta molto rapidamente. Quindi, intorno al punto x = 0, sappiamo che y avrebbe un valore enorme, ma a causa del funzionamento della matematica, non ha un valore definito per quel punto esatto. A volte si dice 1/0 = ∞, ma la realtà è che l'infinito non è un numero ma un concetto.

In questo caso, l'equazione lineare x = 0 rappresenta l'asintoto della funzione y = 1/x, il che significa che y = 1/x non intercetterà mai quella retta e, quindi, non avrà un'intercetta y. In generale, ogni volta che una funzione ha un asintoto che si trova su uno degli assi, sarà mancante di almeno uno dei punti di intercettazione.

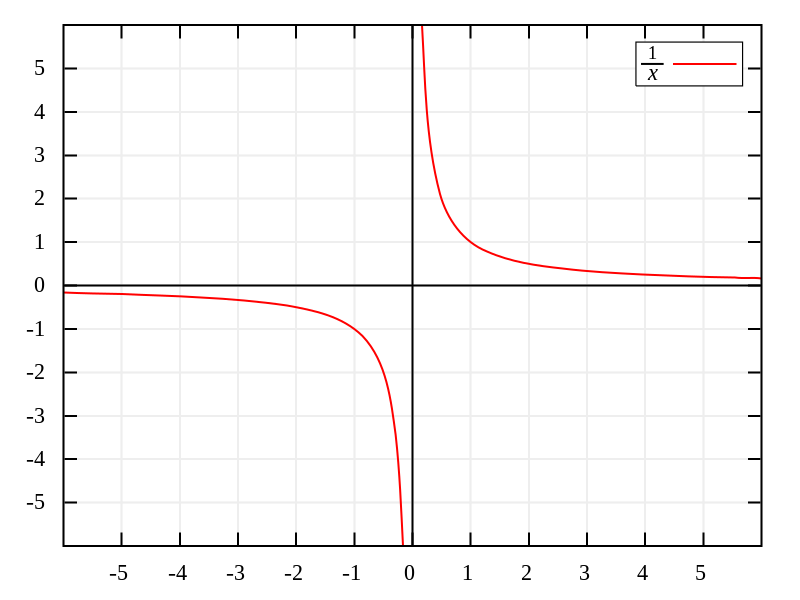
Infatti, anche l'esempio che ti abbiamo mostrato (y = 1/x) ha un asintoto per y = 0, cioè l'asse delle ascisse. Per lo stesso motivo di prima, y = 0 non è mai ottenibile con la formula perché richiederebbe x = ∞ e, come abbiamo detto prima, è impossibile ottenerlo perché l'infinito è un concetto e non un numero.

Prima di passare al prossimo argomento, è importante notare che abbiamo semplificato eccessivamente quando parliamo di infinito, ma riteniamo che sia un approccio valido e veloce per chi non è abituato a lavorare con l'infinito in matematica. Ti consigliamo di approfondire le modalità corrette dell'infinito, a partire dalle forme indeterminate.

Si potrebbe facilmente pensare che l'utilità delle equazioni lineari sia molto limitata a causa della loro semplicità. Tuttavia, la realtà è un po' diversa. Le equazioni lineari sono alla base di alcuni dei metodi più potenti per risolvere problemi di minimizzazione e ottimizzazione.

I problemi di minimizzazione sono un tipo di problema in cui si vuole trovare il modo di ridurre il più possibile una delle variabili. Questa variabile potrebbe essere, ad esempio, la differenza tra una previsione fatta da un modello e la realtà. Questi tipi di problemi sono uno dei problemi più comuni e sono alla base dell'apprendimento automatico (machine learning) e degli esperimenti scientifici.

Uno dei metodi più comuni e potenti per trovare il valore minimo di un'equazione o di una formula è il cosiddetto metodo di Newton, dal nome del genio che lo ha inventato. Funziona utilizzando le derivate, le equazioni lineari e le intercette delle ascisse:

Questo metodo consiste nello scegliere un valore di x per l'equazione e nel calcolare la derivata dell'equazione in quel punto. Utilizzando la derivata come pendenza di un'equazione lineare che passa per quel punto esatto (x, y), si calcola quindi l'intercetta x. Questa è una delle situazioni in cui il modulo dell'intercetta della pendenza si rivela utile.

Una volta calcolata l'intercetta della x, quel valore di x viene utilizzato per ripetere il processo qui sopra, per un numero specifico di volte, fino a raggiungere un valore di y minimo (il che significa che la derivata sarà 0). Nella vita reale, arrivare al punto minimo esatto non è possibile in un tempo finito, quindi in genere ci si accontenta di un valore "abbastanza vicino".

Un esempio molto comune è quando si utilizza il metodo dei minimi quadrati per adattare alcuni dati a una formula o a una tendenza. In questo caso, il valore che vogliamo minimizzare è la somma della distanza al quadrato tra la linea di tendenza e i punti dei dati, dove la distanza viene calcolata lungo una linea perpendicolare dal punto alla linea di tendenza.

No, la forma standard e la forma ad intercetta sono due modi diversi di descrivere una retta:

• La forma pendenza-intercetta si legge y = mx + b, dove m è la pendenza (ripidità) della retta e b è l'intercetta, cioè il valore in cui la retta interseca l'asse verticale. Ad esempio, y = -2x + 3; e
• La forma standard recita Ax + By + C = 0, dove A, B, C sono integri. Ad esempio, 2x + y - 3 = 0.

Se vuoi riscrivere la tua equazione in forma standard nella forma dell'intercetta della pendenza, segui questi passaggi:

1. Scrivi la forma standard della tua retta: Ax + By + C = 0;
2. Sposta Ax e C sul lato destro in modo che By rimanga da solo sul lato sinistro: By = -Ax - C;
3. Dividi entrambi i lati per B: y = -(A/B)x - (C/B); e
4. Come puoi vedere, abbiamo la forma pendenza-intercetta: y = mx + b con pendenza m = -A/B e intercetta b = -C/B.

La pendenza (anche detta gradiente) descrive la ripidità di una linea. La pendenza può essere positiva, negativa o nulla:

• Una pendenza positiva significa che la linea sale da sinistra a destra;
• Pendenza negativa significa che la linea scende da sinistra a destra; e
• Pendenza zero significa che la linea è orizzontale.

Maggiore è il valore assoluto della pendenza, più velocemente la linea aumenta o diminuisce. In effetti, il valore della pendenza è esattamente la quantità di incremento o decremento della retta quando x aumenta di un'unità.

La pendenza è m = 1. Per ottenere questo risultato, usa la formula m = tan(α), dove α è l'angolo tra la retta e l'asse x. Poiché tan(45°) = 1, otteniamo la pendenza 1, come indicato.