Calcolatore del Tasso Medio di Variazione
Indice
Che cos'è il tasso di variazione? — Definizione del tasso medio di variazioneFormula del tasso medio di variazioneCome trovare il tasso medio di variazione? — Primo esempioCome trovare il tasso medio di variazione? — Secondo esempioFAQIl calcolatore del tasso medio di variazione è qui per aiutarti a capire un concetto semplice che si nasconde dietro un nome lungo e un po' confuso. Che cos'è il tasso di variazione? In generale, mostra la relazione tra due fattori. Qui di seguito troverai una definizione più precisa del tasso medio di variazione. Inoltre, ti mostreremo e spiegheremo la formula del tasso medio di variazione con un paio di esempi di utilizzo.
Preferisci guardare piuttosto che leggere? Impara tutto quello che ti serve in 90 secondi con questo video che abbiamo realizzato per te:
Che cos'è il tasso di variazione? — Definizione del tasso medio di variazione
Tutto continua a muoversi. Il cambiamento è inevitabile. A partire dall'accelerazione della tua moto o della tua auto, fino alla crescita della popolazione, dal flusso sanguigno nelle tue vene alla simbiosi delle tue cellule, il tasso di crescita ci permette di stabilire il valore associato a questi cambiamenti.
Il tasso medio di variazione è un tasso che descrive come un numero cambia, in media, rispetto a un altro. Se hai una funzione, è la pendenza della linea tracciata tra due punti. Ma non confonderlo con la pendenza. Puoi utilizzare il tasso medio di variazione per qualsiasi funzione, non solo per quelle lineari.
🙋 Se vuoi saperne di più sulla pendenza, visita il calcolatore del coefficiente angolare.
Formula del tasso medio di variazione
Nell'immagine seguente abbiamo segnato due punti per aiutarti a capire meglio come trovare il tasso medio di variazione.
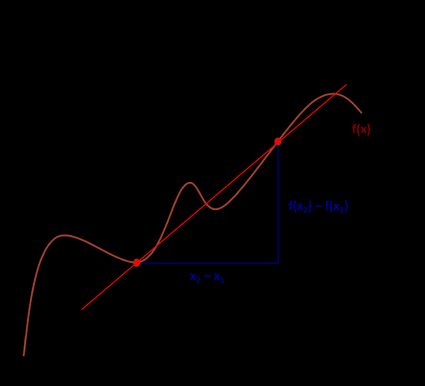
La formula del tasso medio di variazione è:
A = [f(x₂) - f(x₁)] / [x₂ - x₁],
dove:
(x₁, f(x₁))— Coordinate del primo punto; e(x₂, f(x₂))— Coordinate del secondo punto.
Se è positivo, significa che una coordinata aumenta quando aumenta anche l'altra. Ad esempio, più vai in bicicletta, più calorie bruci.
È uguale a zero quando una coordinata cambia ma l'altra no. Un buon esempio potrebbe essere quello di non studiare per gli esami. Quando il tempo inizia a scorrere, la quantità di cose da imparare non cambia.
Il tasso medio di variazione è negativo quando una coordinata aumenta e l'altra diminuisce. Supponiamo che tu stia per andare in vacanza. Più tempo dedichi al viaggio, più ti avvicini alla tua destinazione.
💡 Puoi imparare altri modi per descrivere la differenza tra due punti nel calcolatore della pendenza (rapporto dislivello/lunghezza).
Come trovare il tasso medio di variazione? — Primo esempio
Calcoliamo il tasso medio di variazione della distanza (velocità media) di un treno che va da Parigi a Roma (1420,6 km). Il grafico seguente mostra la variazione della distanza nel tempo:
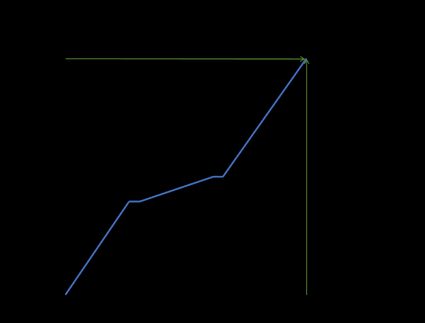
Come vedi, la velocità non era costante. Il treno si è fermato due volte e, tra una fermata e l'altra, è andato significativamente più lento. Ma per calcolare la velocità media, le uniche variabili che contano sono la variazione della distanza e la variazione del tempo. Quindi, se le coordinate del primo punto sono (0, 0) e le coordinate del secondo punto sono la distanza tra due città e il tempo totale — (1420,6, 12,5). Allora:
A = (1420,6 - 0) / (12,5 - 0) = 113,648 [km/h]
In media, il treno andava a 113 648 chilometri all'ora. Vediamo ora un esempio più matematico.
Come trovare il tasso medio di variazione? — Secondo esempio
Ti è stata assegnata una funzione:
f(x) = x² + 5x - 7
Trova il tasso medio di variazione nell'intervallo [-4, 6].
-
Trova i valori della funzione per entrambi i punti:
f(x₁) = f(-4) = (-4)² + 5 × (-4) - 7 = -11f(x₂) = f(6) = 6² + 5 × 6 - 7 = 59; e -
Usa l'equazione del tasso medio di variazione:
A = [f(x₂) - f(x₁)] / [x₂ - x₁] = [f(6) - f(-4)] / [6 - (-4)] = [59 - (-11)] / [6 - (-4)] = 70 / 10 = 7.
Se ti è piaciuto il calcolatore del tasso medio di variazione, non esitare a dare un'occhiata ai nostri altri strumenti come questo calcolatore per la distanza, in cui puoi trovare la distanza tra punti o linee.
Il tasso medio di variazione è uguale alla pendenza?
Non esattamente. Il tasso medio di variazione riflette come una funzione cambia in media tra due punti. D'altra parte, definiamo la pendenza di una funzione come la pendenza della linea tangente alla curva in un punto specifico. In una funzione lineare, ogni punto cambia in modo identico, quindi il tasso medio di variazione e la pendenza sono uguali.
Come si trova il tasso medio di variazione di una funzione?
Per trovare il tasso medio di variazione di una funzione, segui questi passaggi:
-
Ottieni le coordinate (x, y) del punto di partenza. Le chiameremo (x₀, y₀);
-
Ottieni le coordinate (x, y) del punto estremo. Queste saranno (x₁, y₁); e
-
Sostituisci entrambi nella formula del tasso medio di variazione (T):
T = (y₁ - y₀)/(x₁ - x₀).
Qual è il tasso medio di variazione di y = 2x?
Il tasso medio di variazione di y = 2x è 2. Trattandosi di una funzione lineare, il tasso medio di variazione è semplicemente la pendenza della funzione. In questo caso, per ogni variazione della coordinata x, la coordinata y raddoppierà.
La velocità è un esempio di tasso medio di variazione?
Se la velocità è costante, sì. La velocità riflette il modo in cui la posizione cambia costantemente rispetto al tempo. Quindi, se un oggetto si muove a velocità costante, il tasso medio di variazione della posizione ci dice a quale velocità sta viaggiando.