Calcolatore per Vettori
Eccoti nel nostro calcolatore per vettori! Ti aiuterà a eseguire e comprendere un gran numero di operazioni sui vettori. Hai le coordinate cartesiane di due vettori o conosci solo la loro direzione e modulo? Forse devi trovare il vettore tra due punti? Questo calcolatore per vettori è in grado di affrontare tutte queste situazioni; esegue:
- La somma di vettori;
- La sottrazione di vettori;
- La moltiplicazione di vettori(sia prodotto vettoriale che prodotto scalare!); e
- La proiezione vettoriale.
Come bonus, ti insegneremo anche cos'è lo scalare di un vettore e come normalizzare un vettore.
Coordinate cartesiane
In un sistema di coordinate cartesiano, xy, descriviamo il vettore a in un piano 2D con le sue coordinate cartesiane:
a = [ax, ay].
Queste coordinate corrispondono al fatto che possiamo scomporre uno spostamento lungo il vettore a in uno spostamento orizzontale ax lungo l'asse x e uno spostamento verticale ay lungo l'asse y.
Allo stesso modo, descriviamo i vettori nello spazio 3D utilizzando il sistema cartesiano xyz con tre numeri:
a = [ax, ay, az],
che corrispondono agli spostamenti lungo gli assi x, y e z, rispettivamente.
Direzione e modulo del vettore
Possiamo anche descrivere un vettore piano in termini di direzione e modulo del vettore. Il modulo di un vettore è la sua lunghezza e la direzione di un vettore è l'angolo tra l'asse orizzontale e il vettore.
Siano [ax, ay] le coordinate cartesiane di un modulo di un vettore con modulo m e direzione θ. Per convertire un insieme di coordinate nell'altro, usa le seguenti formule:
ax = m × cos(θ)
ay= = m × sin(θ)
Come si determina un vettore tra due punti?
Se devi determinare un vettore tra due punti, cioè dal punto iniziale a quello finale, basta sottrarre le coordinate del punto finale dal punto iniziale:
-
Punto iniziale (origine): a = [ax, ay, az];
-
Punto finale (punta/testa): b = [bx, by, bz]; e
-
Vettore tra questi due punti:
[bx - ax, by - ay, bz - az].
Vediamo un esempio:
-
Punto iniziale:
[1, 2, 3]; -
Punto finale:
[1, 1, -1]; e -
Vettore tra questi due punti:
[1 - 1, 1 - 2, 3 - (-1)] = [0, -1, 4].
Come si calcola lo scalare un vettore?
La normalizzazione vettoriale consiste nello schiacciare/stringere un vettore in modo che abbia un modulo unitario. Ricorda che la direzione di un vettore deve essere mantenuta!
Per normalizzare un vettore, trova lo scalare α utilizzando il teorema di Pitagora. Lo scalare di un vettore è il suo modulo: la radice quadrata della somma dei quadrati delle coordinate del vettore. Dividi quindi ogni coordinata del vettore iniziale per questa norma. Per trovare la norma puoi anche utilizzare il calcolatore del modulo di un vettore 🇺🇸, che è la versione più semplice di questo calcolatore per vettori.
Esempio:
Supponendo che a = [2, 3, 4]. Troviamo lo scalare di a (α):
|a| = √(4 + 9 + 16) = √29
La normalizzazione di a ci dà il vettore a/|a| = [2/√29, 3√29, 4/√29]. Sai che esiste un calcolatore dedicato per la normalizzazione dei vettori?
Come si usa questo calcolatore per vettori?
Per utilizzare il calcolatore per vettori, segui questi passaggi:
- Dicci se stai lavorando con vettori bidimensionali o vettori tridimensionali;
- Decidi l'operazione vettoriale che vuoi eseguire. Puoi scegliere l'addizione o la sottrazione di vettori, la moltiplicazione di vettori (prodotto scalare o vettoriale), la normalizzazione, la proiezione vettoriale o la ricerca del vettore tra due punti;
- Inserisci i tuoi dati. Puoi scegliere tra coordinate cartesiane o direzione e modulo del vettore nel caso di vettori piani; e
- Il nostro calcolatore per vettori restituisce immediatamente i risultati. Buon divertimento! 😊
Somma di vettori
-
In coordinate cartesiane, possiamo eseguire la somma dei vettori semplicemente sommando le componenti corrispondenti dei vettori:
per a = [ax, ay, az],
e b = [bx, by, bz],
abbiamo a + b = [ax + bx, ay + by, az + bz].
Esempio:
La somma di
a = [2, 3, 4]eb = [1, -2, 3]è:a + b = [2 + 1, 3 + (-2), 4 + 3] = [3, 1, 7] -
Metodo grafico: Per due vettori
aeb, se vogliamo ottenere la somma del vettorea + b, posizioniamo l'origine dibsulla punta dia. Il vettore risultante va dall'origine diaalla punta dib. Questa regola viene chiamata regola del parallelogramma:
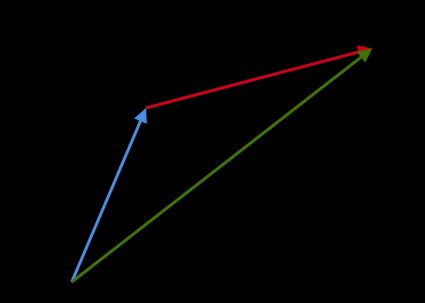
Sottrazione di vettori
La sottrazione del vettore b dal vettore a è semplicemente la somma di -b e a. Per trovare il vettore -b, prendi le coordinate di b con segni opposti; cambia i più in meno e i meno in più:
se b = [1, -2, 4],
allora -b = [-1, 2, -4]
-
Di conseguenza, in coordinate cartesiane, eseguiamo la sottrazione del vettore
a - bsottraendo le coordinate dibda quelle dia:if a = [ax, ay, az]
e b = [bx, by, bz],
allora a - b = [ax - bx, ay - by, az - bz].
Esempio:
La differenza di
a = [2, 3, 4]eb = [1, -2, 3]è data daa - b = [2 - 1, 3 - (-2), 4 - 3] = [1, 5, 1]. -
Metodo grafico: Otteniamo la differenza vettoriale
a - bponendo la punta dibsulla punta diae disegnando un vettore dall'origine diaall'origine dib:
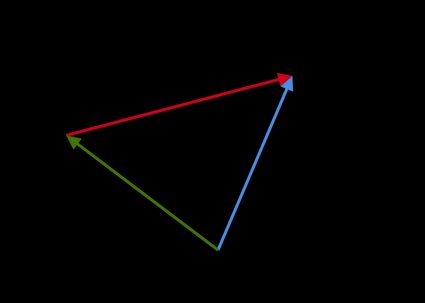
Moltiplicazione di vettori
Fai attenzione quando ti viene chiesto di moltiplicare i vettori: esistono diversi tipi di moltiplicazione vettoriale! Le più diffuse sono il prodotto vettoriale e il prodotto scalare, che descriviamo di seguito:
Moltiplicazione vettoriale — Prodotto vettoriale
Il prodotto vettoriale è un'operazione indicata con l'operatore × e prende due vettori e restituisce un altro vettore.
La formula è la seguente:
a × b = |a| × |b| × sin(θ) × n,
dove:
θ— Angolo traaeb;|a|e|b|— Modulo diaeb; en— Vettore unitario perpendicolare adaeb, determinato dalla regola della mano destra.
Regola della mano destra:
Posiziona la mano destra in modo che l'indice punti sul vettore
ae il medio sul vettoreb: il pollice indica la direzione del prodotto vettorialea × b.
- Interpretazione grafica: Il vettore risultante
a × bè ad angolo retto (perpendicolare) rispetto ai moduli di un vettore iniziale e il suo modulo è pari all'area di un parallelogramma delimitato dai vettori iniziali:
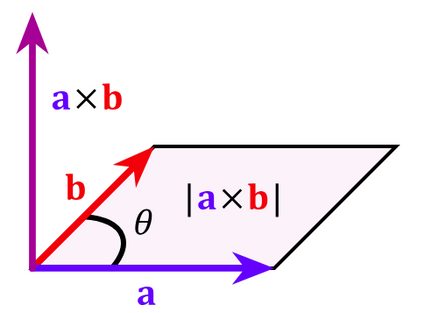
-
In termini di coordinate cartesiane:
per a = [ax, ay, az],
e b = [bx, by, bz], si ha
a × b = [ay×bz - az×by, az×bx - ax×bz, ax×by - ay×bx].
Esempio:
Il prodotto vettoriale di
a = [2, 3, 4]eb = [1, -2, 3]è uguale aa × b = [3 × 3 - 4 × (-2), 4 × 1 - 2 × 3, 2 × (-2) - 3 × 1] = [17, -2, -7]. -
Sì, la formula sembra un po' intimidatoria. È più facile ricordarla una volta capito che le coordinate del prodotto sono i determinanti delle matrici 2 x 2 appropriate:
- La prima coordinata è:


- La terza coordinata è:

-
Fai attenzione all'ordine dei vettori perché, a differenza del prodotto scalare, per il prodotto vettoriale l'ordine conta! Più precisamente, si ha
b × a = - a × b, quindi se hai sbagliato l'ordine, basta cambiare il segno e tutto sarà a posto. 🙃 -
Puoi trovare ulteriori dettagli e informazioni interessanti sul prodotto vettoriale nel nostro articolo intitolato “Prodotto vettoriale di due vettori 🇺🇸”. (*Disponibile in inglese)
-
Il prodotto vettoriale ha molte applicazioni in fisica e ingegneria. Ad esempio, puoi usarlo per determinare la forza di Lorentz 🇺🇸. Dai un'occhiata al nostro calcolatore per il prodotto vettoriale 🇺🇸 per saperne di più!
Moltiplicazione vettoriale — Prodotto scalare
Il prodotto scalare è un'operazione indicata dall'operatore · che prende due vettori e restituisce un numero. Dati due vettori a e b, il loro prodotto scalare è il prodotto dei loro moduli (norme) |a| e |b| e il coseno dell'angolo θ tra loro:
a · b = |a| × |b| × cos(θ).
-
In coordinate cartesiane, il prodotto scalare è la somma dei prodotti delle coordinate corrispondenti dei due vettori:
a · b = ax × bx + ay × by + az × bz.
Esempio:
Il prodotto scalare di
a = [2, 3, 4]eb = [1, -2, 3]èa · b = 2 × 1 + 3 × (-2) + 4 × 3 = 2 - 6 + 12 = 8. -
Come avrai già capito dalla formula, l'ordine non ha importanza in questo caso:
a · b = b · a. -
Astuzia: Se calcoli il prodotto scalare di due vettori uguali, otterrai il modulo del vettore al quadrato:
a · a = |a|²! -
Per maggiori dettagli, consulta il nostro calcolatore per il prodotto scalare 🇺🇸.
Proiezione vettoriale
La proiezione di b su a è il vettore che rappresenta la migliore approssimazione di b tra i vettori ottenuti allungando e comprimendo il vettore a. Quindi, per trovare la proiezione, è sufficiente conoscere il fattore di compressione.
-
Formula:
La proiezione di
bsuaè il vettoreascalato di:a · b / |a|².Esempio:
Sia
a = [2, 3, 4]eb = [1, -2, 3]. Calcoliamo la proiezione dibsua. Per prima cosa, troviamo il fattore di scala. Abbiamo calcolato sopra chea · b = 8e|a| = √29. Di conseguenza, la proiezione dibsuaè:8/29 × [2, 3, 4] = [16/29, 24/29, 32/29] -
Per trovare la proiezione di
bsuagraficamente, devi scomporrebin un vettore lungo l'asse diae un altro perpendicolare ada. La componente che si trova lungoaè la proiezione dibsua. Puoi anche pensare a questa componente come l'ombra che il vettorebproietterebbe sul vettorease ci fosse una fonte di luce appesa sopra questi vettori:
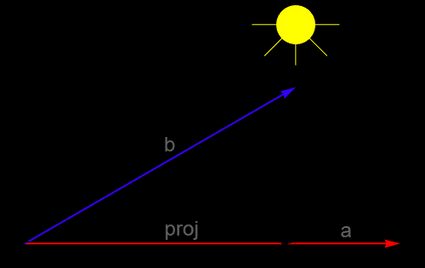
Per saperne di più sulla proiezione di vettori su altri vettori, vai al nostro calcolatore della proiezione vettoriale 🇺🇸.
FAQ
Che cos'è un vettore?
Un vettore è un oggetto matematico definito da:
- Un modulo; e
- Una direzione.
Sono sostanzialmente diversi dalle quantità scalari: queste ultime non cambiano con la direzione.
I vettori hanno applicazioni molto diffuse in fisica, dove si adattano a quantità come lo spostamento e la velocità.
Come si trova la proiezione di un vettore su un altro?
Se consideri i vettori a e b, puoi trovare la proiezione di a su b seguendo questi passaggi:
- Calcola il prodotto scalare di a e b: a · b;
- Calcola il prodotto scalare di b per se stesso: b · b;
- Calcola il rapporto tra i due risultati: (a · b)/(b · b); e
- Moltiplica il risultato per il vettore b: [(a · b)/(b · b)] × b.
Qual è il prodotto scalare di due vettori?
Il prodotto scalare di due vettori è un'operazione che consiste nel sommare il prodotto delle componenti di due vettori.
Se hai due vettori, a = (a₁, a₂, a₃, ..., an) e b = (b₁, b₂, b₃, ..., bn), segui questi due passaggi per calcolare il prodotto scalare:
- Calcola il prodotto di ogni coppia di componenti: a₁ × b₁, a₂ × b₂, ecc; e
- Somma i risultati: (a₁ × b₁) + (a₂ × b₂).
Nota che puoi calcolare solo il prodotto scalare di vettori con lo stesso numero di componenti.
Qual è il modulo di un vettore con componenti (3,1,4,1,5)?
Per calcolare il modulo di un vettore con componenti (3,1,4,1,5), applica il teorema di Pitagora generalizzato a tutte le componenti. Se il vettore è a = (a₁, a₂, a₃, ..., an), troviamo il modulo con la seguente formula:
||a|| = √(a₁² + a₂² + a₃² + ... + an²).
Nel caso del vettore 3,1,4,1,5, il modulo è:
√(3² + 1² + 4² + 1² + 5²) = √(9+1+16+1+25) = √(52) ≈ 7,21.
