Calcolatore per la Somma dei Vettori

Eccoti nel calcolatore per la somma dei vettori di Omni, dove impareremo tutto sulla somma di vettori in 2D o 3D. Il nostro strumento ci permette di dare ai due vettori le coordinate cartesiane o la magnitudine e l'angolo. Come bonus, può prendere alcuni multipli dei vettori o funzionare come calcolatore per la sottrazione di vettori. Per le volte in cui non hai a portata di mano lo strumento di Omni, ti forniamo la formula dell'addizione vettoriale e descriviamo in dettaglio come sommare i vettori usando la regola del parallelogramma.

Preferisci guardare piuttosto che leggere? Dai un'occhiata alla nostra videolezione sulla sottrazione e l'addizione del vettore qui:

Da un punto di vista matematico, un vettore è una sequenza ordinata di numeri (una coppia in 2D, una tripla in 3D e più in dimensioni superiori) e non c'è altro da dire. Naturalmente, gli scienziati non sarebbero loro stessi se si limitassero a questo, quindi hanno ampliato questa definizione. In generale, un vettore è un elemento di uno spazio vettoriale, punto. Questa spiegazione sembra abbastanza semplice finché non scopriamo che, per i matematici, gli spazi vettoriali possono essere costituiti da sequenze, funzioni, permutazioni, matrici, ecc. Fortunatamente, in questo calcolatore per la somma dei vettori non abbiamo bisogno di nulla di tutto ciò.

D'altra parte, i fisici preferiscono pensare ai vettori come frecce (che sono la loro rappresentazione visiva) attaccate agli oggetti. In quanto tali, rappresentano le forze che agiscono su un oggetto, che si tratti di gravitazione, forza frenante o attrazione magnetica. La direzione di una freccia ci dice la direzione della forza, mentre la sua lunghezza indica l'entità della forza.

Fortunatamente, entrambi gli approcci sono essenzialmente la stessa cosa, almeno nel nostro caso e in questo calcolatore per la somma dei vettori. Tuttavia, possiamo rappresentare i vettori in due modi: utilizzando le coordinate cartesiane o il modulo e l'angolo. Tuttavia, quest'ultimo è possibile solo nel caso bidimensionale poiché corrisponde, di fatto, ad avere coordinate polari.

Vediamo un esempio. Un vettore v= (2,1) vive in 2D (poiché ha due coordinate) e ci dice, in sostanza, che "segue due passi lungo l'asse X e un passo lungo l'asse Y". Nota che le coordinate positive si traducono in un viaggio verso destra e verso l'alto (rispettivamente lungo l'asse orizzontale e verticale), mentre le negative indicano la direzione opposta. Allo stesso modo, se aggiungiamo una terza coordinata, ad esempio w= (2,1,5), ci ritroveremo in 3D e il 5 in più corrisponde al movimento lungo l'asse Z.

In alternativa, possiamo rappresentare il vettore bidimensionale v utilizzando il suo modulo m e la sua direzione θ. La prima è semplicemente la lunghezza del vettore. La seconda è l'angolo che va in senso antiorario dalla metà positiva dell'asse orizzontale al vettore quando viene disegnato sul piano con il punto di partenza in (0,0).

In particolare, ciò significa che m deve essere non negativo, mentre θ deve essere compreso tra 0 e 360 gradi (o tra 0 e 2π in radianti), anche se questo calcolatore per la somma dei vettori accetta altri valori dell'angolo secondo le stesse regole che governano le funzioni trigonometriche e i loro argomenti.

Ricordiamo che esiste un equivalente delle coordinate polari (modulo e direzione) in 3D chiamato coordinate sferiche. Tuttavia, esse tendono a essere disordinate e sono molto meno comuni nella pratica, quindi le evitiamo nel nostro calcolatore per la somma dei vettori. Tuttavia, puoi saperne di più nel nostro calcolatore per il sistema sferico di coordinate 🇺🇸.

Bene, abbiamo imparato a conoscere abbastanza bene l'oggetto con cui abbiamo a che fare. È arrivato il momento di prenderne un paio e vedere una descrizione di come addizionare i vettori.

La somma dei vettori è facile, soprattutto se si tratta di coordinate cartesiane. Per essere precisi, dobbiamo semplicemente sommare i numeri in senso coordinato. Ciò significa che la formula della somma dei vettori in 2D è la seguente:

(a,b) + (d,e) = (a + d, b + e),

e quella in 3D è

(a,b,c) + (d,e,f) = (a + d, b + e, c + f).

È tutto qui, non ci sono vincoli. È bello avere una formula semplice, giusto per cambiare, vero?

In 2D, se utilizziamo la rappresentazione del modulo e della direzione, la cosa si fa un po' più complicata. Purtroppo, in questo caso, non possiamo semplicemente sommare i valori dei due vettori come abbiamo fatto con le coordinate cartesiane. La legge del parallelogramma viene spiegata visivamente in modo eccellente nella prossima sezione.

Tuttavia, supponiamo che tu non abbia voglia di disegnare i vettori. In questo caso, il modo migliore per trovare la loro somma in questa forma è semplicemente trovare la loro rappresentazione in coordinate cartesiane e utilizzare la formula della somma dei vettori che trovi all'inizio di questa sezione.

Certamente, è utile che il passaggio da una all'altra sia relativamente semplice. Per essere precisi, se un vettore v ha modulo m e direzione θ, allora v= (x,y) in coordinate cartesiane con:

x = m × cos(θ) e y = m × sin(θ),

dove cos e sin sono rispettivamente le funzioni trigonometriche coseno e seno (per saperne di più consulta il calcolatore delle funzioni trigonometriche 🇺🇸). Per completezza, citiamo anche la formula di transizione dalle coordinate polari a quelle cartesiane:

m = √(x² + y²) e θ = arccos(x / m),

dove arccos è la funzione coseno inversa (maggiori informazioni nel nostro calcolatore dell'arcoseno 🇺🇸).

Prima di mostrarti la regola del parallelogramma, menzioniamo un paio di funzionalità bonus del calcolatore per la somma dei vettori.

1. Calcolatore per la sottrazione di vettori
   Gli diamo un nome così elegante, ma si riduce a un cambiamento super semplice. Per essere precisi, invece di sommare vettori, potresti voler trovare la loro differenza. Le regole sono le stesse di prima: sottraiamo i vettori in modo coordinato. Per utilizzare questa opzione, scegli semplicemente Sottrazione alla nel campo Operazione dello strumento, e questo si trasformerà in un calcolatore per la sottrazione dei vettori; e

2. Somma di vettori con multipli
   Può capitare che tu voglia addizionare un vettore non una ma diverse volte. Ad esempio, v+ 4 ×w significa addizionare quattro copie di w a v. Invece di usare il calcolatore per la somma dei vettori quattro volte per trovare il risultato, puoi cambiare senza multipli in con multipli e inserire i valori di α e β. Naturalmente, puoi calcolare questa opzione con il punto 1 e ottenere un calcolatore per la sottrazione vettoriale con multipli.

Nella prima sezione, abbiamo detto che rappresentiamo i vettori come frecce. Finora li abbiamo trattati solo algebricamente, come nella formula della somma dei vettori. Ora è arrivato il momento di tornare a disegnare. Disegnare parallelogrammi, per essere precisi.

In sostanza, sommare i vettori significa viaggiare lungo uno di essi e poi lungo l'altro. Ciò significa che se ne disegniamo uno come una freccia, il "viaggiare" lungo di esso si traduce nello spostarsi (come punto) dal suo punto di partenza all'estremo. Se vogliamo spostarci con la seconda freccia da lì, possiamo semplicemente disegnarla a partire dal primo estremo e il luogo in cui punta la freccia sarà il nostro risultato.

Sopra abbiamo descritto l'idea che sta alla base della somma di vettori in modo visivo ed è anche ciò su cui si basa la regola del parallelogramma. È solo un modo più elegante di metterla in pratica. Ovvero, la somma di due vettori è la diagonale di un parallelogramma i cui lati sono i due vettori sommati se disegnati a partire dallo stesso punto.

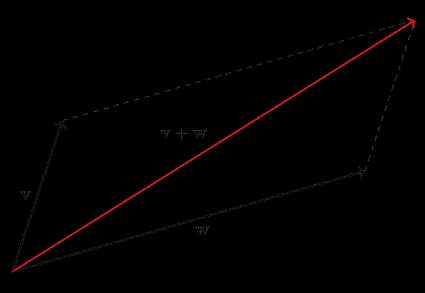
Nell'immagine, possiamo spostarci dal vertice in cui v e w iniziano al vertice opposto percorrendo prima v e poi w, o viceversa (il secondo passo è rappresentato da una linea tratteggiata). È la stessa cosa che abbiamo fatto all'inizio di questa sezione. Nota anche che l'ordine in cui ci muoviamo non ha molta importanza perché l'addizione è commutativa.

E con questo, concludiamo la parte teorica per oggi. Ora passiamo a utilizzare tutte queste conoscenze e vediamo come funziona in pratica il calcolatore per la somma dei vettori.

Supponiamo di voler trovare la somma di un vettore v= (-3,2,8) e tre copie di w= (2,2,-4). Prima di farlo a mano, vediamo come utilizzare il calcolatore per la somma dei vettori per trovare la risposta.

Innanzitutto, ricordiamo che stiamo sommando vettori con tre coordinate (cartesiane), quindi sono tridimensionali. Pertanto, dobbiamo scegliere 3D nel campo Vettori in e Addizione nel campo Operazione. Questo ci mostrerà due sezioni per le coordinate, ciascuna con tre campi variabili contrassegnati da x, y e z, che corrispondono rispettivamente alla prima, alla seconda e alla terza coordinata. Pertanto, nella sezione che descrive v = (-3,2,8), inseriamo:

x = -3, y = 2, z = 8,

e in quella di w= (2,2,-4), scriviamo:

x = 2, y = 2, z = -4.

Una volta inserito l'ultimo valore, possiamo vedere v + w nella sezione Risultato. Tuttavia, non è proprio quello che ci serve, vero? Vorremmo sommare tre copie di w e non una.

Pertanto, scegliamo l'opzione con multipli nella parte superiore del calcolatore, che calcolerà α ×v+ β ×w invece di v + w. Nota che abbiamo già inserito α = 1 e β = 1 come valori predefiniti. Per il nostro problema, li cambiamo in:

α = 1, β = 3,

che ci fornirà la soluzione finale. Tuttavia, prima di rivelarla, usiamo la formula della somma dei vettori e troviamo la somma da soli.

Osserva che sommare tre copie di un vettore significa sommare tre volte le sue coordinate. Pertanto,

v+ 3 ×w= (-3,2,8) + 3 × (2,2,-4) = (-3 + 3 × 2, 2 + 3 × 2, 8 + 3 × (-4)) = (3,8,-4).

Voilà! Questa potrebbe essere una singola riga di calcolo, ma riesci a immaginare di fare tutto questo con delle voci terribilmente complicate? Per fortuna c'è il calcolatore di Omni per la somma dei vettori che ci fa risparmiare tempo e fatica.

La somma dei vettori x = (x₁, x₂, ..., x_k) e y = (y₁, y₂, ..., y_k) è uguale a:

x + y = (x₁ + y₁, x₂ + y₂, ..., x_k+ y_k).

In altre parole, eseguiamo l'addizione in senso coordinato. In particolare, per i vettori a 2 dimensioni, otteniamo:

(x₁, x₂) + (y₁, y₂) = (x₁ + y₁, x₂ + y₂).

Per eseguire la somma di vettori:

1. Somma le coordinate della prima posizione: 2 + 1 = 3;
2. Somma le coordinate della seconda posizione: 1 + 0 = 1;
3. Scrivi i risultati dei passi 1 e 2: (3,1); ed
4. Ecco fatto! Hai appena eseguito con successo una somma di vettori!

La formula del modulo di x + y = (x₁ + y₁, x₂ + y₂) è la seguente:

|x + y| = √[(x₁ + y)²+(x₂ + y₂)²].

Come avrai sicuramente notato, utilizza il teorema di Pitagora!

La formula dell'angolo di direzione della somma di vettori x + y = (x₁ + y₁, x₂ + y₂) è:

θ = arctan((x₂ + y₂)/(x₁ + y₁)),

dove arctan indica la funzione arcotangente (tangente inversa).