Calcolatore per lo Sfasamento

Eccoti nel calcolatore per lo sfasamento di Omni, dove studieremo le funzioni trigonometriche e come calcolare il loro sfasamento. In realtà, non ci limiteremo a questo: spiegheremo anche come trovare l'ampiezza e come trovare il periodo. In realtà, è emerso che un'enorme classe di funzioni si comporta praticamente allo stesso modo e le differenze si riducono alla descrizione dei valori sopra citati; l'ampiezza, il periodo e lo sfasamento. Almeno fino a uno spostamento verticale.

Come abbiamo detto sopra, ci concentreremo qui sulle funzioni trigonometriche: nello specifico sul seno e sul coseno. Tuttavia, è importante ricordare che molte nozioni sono più generali, soprattutto quelle di traslazione orizzontale o di spostamento verticale.

Prima di tutto, vediamo un'immagine che mostra dove l'ampiezza, il periodo, lo sfasamento e lo spostamento verticale appaiono sul grafico (nota che la stessa immagine appare nella parte superiore del calcolatore per lo spostamento di fase di Omni).

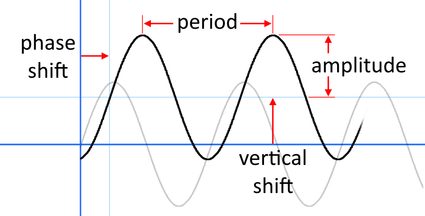
Possiamo scrivere tali funzioni con la formula (a volte chiamata equazione di sfasamento o formula di sfasamento):

oppure:

dove $A$, $B$, $C$, $D$ sono numeri reali arbitrari, ma con $A$ e $B$ non nulli (altrimenti non sarebbe una funzione trigonometrica). Ovviamente, questi quattro numeri determinano l'ampiezza, il periodo, lo sfasamento e lo spostamento verticale. In un certo senso, l'immagine suggerisce come influiscono sul grafico. Tuttavia, sarebbe utile supportare le immagini con alcune definizioni.

1. L'ampiezza è la distanza (in entrambi i sensi) dei valori dalla linea centrale del grafico. Per un semplice seno o coseno, il suo valore è $1$ poiché la linea centrale si trova a $0$, e i valori della funzione vanno da $-1$ a $1$;

2. Il periodo è la lunghezza sull'asse orizzontale dopo la quale la funzione inizia a ripetersi. In altre parole, il grafico (infinito) è solo un insieme di copie della lunghezza del periodo incollate insieme alle estremità. Per un semplice seno o coseno, il periodo è uguale a $2\pi$ poiché $\sin(0) = \sin(2\pi) = \sin(4\pi) = ...$ e le parti intermedie sono esattamente le stesse (e lo stesso vale per il coseno);

3. Lo sfasamento (chiamato anche spostamento orizzontale o traslazione orizzontale) descrive quanto il grafico è stato spostato orizzontalmente rispetto al seno o al coseno regolari. Per questo motivo, il valore è uguale a $0$ se le due funzioni sono inalterate; e

4. Lo spostamento verticale (chiamato anche traslazione verticale) descrive lo spostamento verticale del grafico rispetto al seno o al coseno regolari. In altre parole, è il gemello dello sfasamento che riguarda la direzione perpendicolare. In particolare, il valore è di nuovo uguale a $0$ se le due funzioni sono inalterate.

Bene, abbiamo imparato cos'è lo sfasamento e i tre valori che lo accompagnano. Le sezioni seguenti descrivono come calcolare ciascuno di essi basandosi sulla notazione della formula dello sfasamento di cui sopra. Per prima cosa, mostriamo come trovare l'ampiezza.

Il concetto che abbiamo introdotto è molto diffuso nello studio dei moti oscillatori e armonici. Per dirla tutta, questi fenomeni sono i migliori amici della trigonometria. Puoi scoprire il collegamento con il nostro calcolatore per la trigonometria o saperne di più sulle varie funzioni che compaiono quando analizzi un pendolo con il calcolatore delle funzioni trigonometriche 🇺🇸 — o con quelli più specifici; calcolatore del coseno 🇺🇸 e calcolatore del seno 🇺🇸!

Sappiamo che le funzioni seno e coseno hanno valori compresi tra $-1$ e $1$. Inoltre, questo semplice fatto non cambia se sostituiamo $\sin(x)$ o $\cos(x)$ con $\sin(Bx - C)$ o $\cos(Bx - C)$ con un $B$ non nullo e $C$ arbitrario. Infatti, la funzione $f(x) = Bx - C$ è una biiezione (cioè una corrispondenza uno a uno) sullo spazio dei numeri reali.

Ora vediamo cosa succede se aggiungiamo $D$, cioè se abbiamo $\sin(Bx - C) + D$ o $\cos(Bx - C) + D$. Dal momento che la prima parte dà qualcosa tra $-1$ e $1$, l'intera cosa sarà compresa tra $-1 + D$ e $1 + D$ (vedi Come trovare lo spostamento verticale per un confronto). Ciò significa che la linea centrale cade a $D$, e l'ampiezza è ancora $1$ perché i valori cadono fino a $1$ lontano da $D$.

Pertanto, l'unica cosa che può influenzare l'ampiezza nelle formule di sfasamento $A\times\sin(Bx - C) + D$ e $A\times\cos(Bx - C) + D$ è il valore non nullo $A$. Infatti, poiché $\sin(Bx - C)$ e $\cos(Bx - C)$ si trovano tra $-1$ e $1$, il moltiplicatore $A$ cambia questo intervallo in $-1\times A = -A$ e $1 \times A = A$.

Sì, hai indovinato: l'ampiezza delle equazioni di sfasamento $A \times\sin(Bx - C) + D$ e $A \times\cos(Bx - C) + D$ è semplicemente uguale a $A$.

Ricordiamo che le funzioni seno e coseno hanno periodi uguali a $2\pi$, cioè abbiamo $\sin(x + 2\pi) = \sin(x)$ e $cos(x + 2\pi) = cos(x)$ per qualsiasi $x$. In particolare, questo dà:

e:

Quindi, vediamo che $A$ e $D$ nella formula dello sfasamento non hanno alcun effetto sul periodo. In effetti, tutto si riduce a quello che succede all'interno delle funzioni trigonometriche. Eppure:

e:

Secondo le stesse regole di cui sopra, quindi non è néache il $C$ a fare il lavoro. Quindi, avendo scartato tre opzioni, deve essere la quarta: il $B$.

Torniamo ancora una volta al commento con cui abbiamo iniziato per capire come mai, e come $B$ può influire sulla periodicità nelle equazioni di sfasamento $A \times \sin(Bx - C) + D$ e $A \times \cos(Bx - C) + D$. Dopo tutto:

Quindi, ad ogni $2\pi/B$ aggiunto all'argomento $x$, arriviamo allo stesso punto e la funzione si ripete (e lo stesso vale per il coseno).

In definitiva, il periodo di un'equazione di sfasamento è uguale a $2\pi/B$.

La nostra conoscenza quotidiana delle onde di solito privilegia la frequenza rispetto al periodo; tuttavia, sono quasi la stessa cosa. Scopri il perché su calcolatore di frequenza di Omni.

Per definizione, lo sfasamento descrive la traslazione orizzontale della funzione rispetto al $\sin(x)$ o al $\cos(x)$ regolare. Per questo motivo, le funzioni di base lo hanno uguale a $0$. Infatti, se confrontiamo i loro grafici:

...noteremo che possiamo ottenere una traducendo l'altra (infatti, le cofunzioni reciproche hanno molte analogie). Per essere precisi, abbiamo quanto segue:

e:

L'esempio precedente ci suggerisce già dove cercare in $A \times\sin(Bx - C) + D$ e $A \times\cos(Bx - C) + D$, i valori responsabili degli sfasamenti. Tuttavia, a differenza dall'ampiezza e il periodo, questa volta avremo bisogno di due delle quattro lettere.

In generale (cioè non solo nelle equazioni di sfasamento), otteniamo la traslazione orizzontale di una funzione arbitraria $f(x)$ calcolando $f(x - a)$: lo spostamento del grafico di $a$ verso destra. In altre parole, sostituiamo ogni occorrenza di $x$ con $x - a$ nella formula per $f(x)$. Ad esempio, applicando la traduzione a $\sin(x)$ si ottiene $\sin(x - a)$, ma per esempio per $\cos(3x + 1)$ otterremmo:

In altre parole, non possiamo dimenticare i moltiplicatori che si trovano di fronte a $x$.

Nel nostro caso, la formula dello sfasamento dà:

che è uno sfasamento $C/B$ (verso destra) della funzione $A \times\sin(Bx)$. Naturalmente, possiamo ripetere quanto detto sopra anche per il coseno.

Per riassumere, per calcolare lo sfasamento di un'equazione di sfasamento, devi trovare $C/B$.

Questo è facile, soprattutto ora che abbiamo visto cosa sono lo sfasamento, l'ampiezza e il periodo e come calcolarli. Facciamo tesoro di ciò che abbiamo imparato finora.

Sappiamo che nelle formule di sfasamento $A \times\sin(Bx - C) + D$ e $A \times\cos(Bx - C) + D$, il parametro $A$ determina quanto i valori fluttuano su entrambi i lati della linea centrale. $B$ specifica quanto si estendono le asperità del grafico e, di conseguenza, la velocità di ripetizione dei valori. Inoltre, insieme a $C$, i due descrivono se abbiamo spostato la funzione a sinistra o a destra e di quanto.

Ovviamente, la traslazione orizzontale non influisce sullo spostamento verticale: si tratta di due direzioni perpendicolari, dopotutto. D'altra parte, l'ampiezza ci dice solo quanto si estende in verticale il grafico, ma non lo sposta. In definitiva, ci rimane solo una lettera: $D$.

Il $D$ nelle equazioni dello sfasamento è proprio lo spostamento verticale. Determina l'intervallo della funzione, cioè quanto lontano dalla versione abituale e non$D$ spostiamo il grafico.

Questo conclude la parte teorica per oggi. È arrivato il momento di vedere come calcolare lo sfasamento su un bell'esempio. E sai cosa? Mostreremo anche come trovare il periodo, l'ampiezza e lo spostamento verticale. Dopotutto, perché no? Più calcoli matematici = più divertimento!

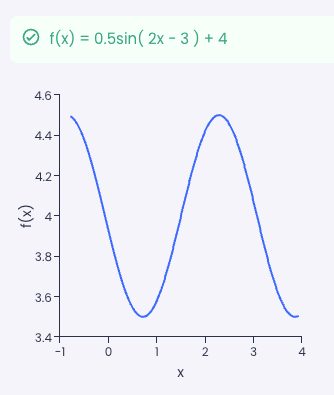
Vediamo come trovare l'ampiezza, il periodo, lo sfasamento e lo spostamento verticale della funzione $f(x) = 0,\!5 \times\sin(2x - 3) + 4$. Per prima cosa, lasceremo che sia il calcolatore per lo spostamento di fase di Omni a parlare.

Nella parte superiore del nostro strumento, dobbiamo scegliere la funzione che compare nella nostra formula. Nel nostro caso, scegliamo Seno sotto La funzione trigonometrica in f. In questo modo si attiverà una rappresentazione simbolica dell'equazione dello sfasamento: $f(x) = A \times\sin(Bx - C) + D$. Guardando quello che abbiamo, inseriamo quanto segue:

Si noti che prima ancora di inserire i valori, il calcolatore per lo sfasamento visualizza il grafico della funzione $\sin(x)$. Ciò è dovuto al fatto che lo strumento interpreta la non indicazione di alcuni valori come l'assenza di numeri nei punti corrispondenti della formula. Per questo motivo, legge l'assenza di input come $A = 1$, $B = 1$, $C = 0$ e $D = 0$, che dà come risultato:

Nel momento in cui diamo l'ultimo valore, il grafico della funzione appare sotto insieme all'ampiezza, al periodo, allo spostamento di fase e allo spostamento verticale più in basso. Inoltre, se necessario, è possibile accedere alla Modalità avanzata del calcolatore per trovare il valore della funzione in qualsiasi punto $x_0$.

Ora spieghiamo come trovare da soli lo sfasamento e tutti gli altri valori. A tal fine, è sufficiente ricordare le quattro sezioni precedenti per calcolare che:

• L'ampiezza è $A = 0,\!5$;
• Il periodo è $2\pi / B = 2\pi / 2 = \pi$;
• Lo spostamento di fase è $C / B = 3 / 2 = 1,\!5$; e
• Lo spostamento verticale è $D = 4$.

Nel complesso, il grafico ha questo aspetto:

Un gioco da ragazzi, vero? Assicurati di giocare con il calcolatore per lo sfasamento per vedere come i diversi coefficienti influenzano il grafico.

Per calcolare lo sfasamento di una funzione della forma A × sin(Bx - C) + D o A × cos(Bx - C) + D, devi:

1. Determinare B;
2. Determinare C;
3. Dividere C/B;
4. Ricordare che se il risultato è:
   • Positivo, il grafico viene spostato a destra,
   • Negativo, il grafico viene spostato a sinistra; e
5. Godere il tuo successo.

Per trovare lo sfasamento da un grafico:

1. Determina se si tratta di un seno o di un coseno spostato;
2. Osserva il grafico a destra dell'asse verticale;
3. Trova la prima:
   • Cresta se il coefficiente prima della funzione è positivo, oppure
   • Gola se il coefficiente è negativo;
4. Calcola la distanza dalla linea verticale a quel punto;
5. Se la funzione era un seno, sottrai π/2 o 3π/2 da quella distanza per ottenere rispettivamente un picco o un avvallamento; e
6. Goditi l'aver trovato lo spostamento di fase da un grafico.

Trovare l'ampiezza, il periodo e lo spostamento di fase di una funzione della forma A × sin(Bx - C) + D o A × cos(Bx - C) + D si fa come segue:

• L'ampiezza è uguale ad A;
• Il periodo è uguale a 2π / B; e
• Lo spostamento di fase è pari a C / B.

Per grafare le funzioni trigonometriche con lo sfasamento:

1. Determina la funzione trigonometrica;
2. Focalizza il punto (0,0) sul piano;
3. Se lo sfasamento è:
   • Positivo, spostati a destra,
   • Negativo, spostati a sinistra;
4. Spostati della distanza data dallo sfasamento;
5. Il punto trovato è il tuo punto di partenza;
6. Disegna il grafico della funzione non spostata come se il punto fosse (0,0); e
7. Goditi il grafico di una funzione trigonometrica con uno spostamento di fase.

Quando si tratta di funzioni trigonometriche, sì. Di solito riserviamo il termine "sfasamento" alle funzioni trigonometriche. In altre parole, possiamo avere uno spostamento orizzontale di qualsiasi grafico o funzione. Tuttavia, quando si tratta di una funzione trigonometrica, possiamo definire lo spostamento orizzontale come uno sfasamento.